
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теория вероятностей и закон больших чисел.
Статистической совокупностью называют группу, состоящую из множества относительно однородных элементов, взятых вместе в известных границах времени и пространства. Каждая статистическая совокупность может рассматриваться как генеральная или как выборочная, от этого зависит интерпретация результатов исследования. Теоретическое обоснование выборочному методу дает математическая теория вероятностей и обосновываемый этой теорией закон больших чисел. Теория вероятностей рассматривает меру возможности (вероятности) появления в изучаемой группе какого-либо признака, который математики называют случайным событием. Например, несмотря на случайность каждого отдельного посещения больным поликлиники, в общей массе эти посещения распределяются изо дня в день по часам суток с определенной закономерностью, так что попредыдущим дням можно судить с наибольшей вероятностью о численности посещений, которые сделают больные в поликлинику в различные часы в последующие дни. Вероятностью называют меру возможности возникновения каких-либо случайных событий в данных конкретных условиях и обозначают ее буквой «p». Вероятность наступления в выборочной совокупности какого-либо события «p» определяется отношением наступивших событий (m) к числу всех возможных случаев (n): В противоположность вероятности наступившего события различают альтернативу – вероятность отсутствия события, которая обозначается «:q»
q = 1- p; p + q = 1. Вероятность наступления события «p» находится в границах от 0 до 1. Чем ближе вероятность события к единице, тем событие вероятнее, и, наоборот, чем ближе «p» к нулю, тем наступление события менее вероятно, т.е. оно может отсутствовать.  Теория вероятностей обосновывает закон больших чисел. Закон больших чисел имеет два важнейших положения для выборочного исследования: а) по мере увеличения числа наблюдений результаты исследования, полученные на выборочной совокупности, стремятся воспроизвести данные генеральной совокупности; б) при достижении определенного числа наблюдений в выборочной совокупности результаты исследования будут максимально приближаться к данным генеральной совокупности, т.е. при достаточно большом числе наблюдений выявляются закономерности, которые не удается обнаружить при малом числе наблюдений.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 742. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
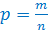 ,
, ;
;