
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференциальные уравнения высших порядков3.2.1 Дифференциальные уравнения вида (задание 9) Найти общее решение дифференциального уравнения второго рода, используя соответствующую замену.
Частным случаем дифференциальных уравнений вида Для решения необходимо понизить порядок дифференциального уравнения, проинтегрировав правую и левую его части Пример 41 Найти общее решение дифференциального уравнения Решение
Дифференциальные уравнения вида Пример 42 Найти общее решение дифференциального уравнения Решение
Пример 43 Найти общее решение дифференциального уравнения Решение
Так как Заменим 
Таким образом, исходное дифференциальное уравнение имеет общее решение 3.2.2 Дифференциальные уравнения вида (задание 10)
Найти решение задачи Коши дифференциального уравнения второго рода, используя соответствующую замену.
Дифференциальные уравнения вида Пример 44 Найти решение задачи Коши дифференциального уравнения Решение
Можно заметить, что случай Теперь, воспользуемся подстановкой
Заменим В полученное уравнение остаётся подставить дополнительное условие задачи Коши Итак, частное решение задачи Коши для искомого уравнения имеет вид |
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 230. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
. . Полученное уравнение необходимо снова проинтегрировать.
. Полученное уравнение необходимо снова проинтегрировать. .
. ,
, ,
, ,
, ,
,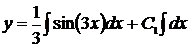 ,
, ,
, .
.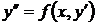 ) решаются с помощью замены
) решаются с помощью замены  , где
, где  новая неизвестная функция. Тогда
новая неизвестная функция. Тогда  . Исходное уравнение примет вид
. Исходное уравнение примет вид  дифференциальное уравнение первого порядка.
дифференциальное уравнение первого порядка. .
. ,
, ,
, ,
, ,
, ,
, ,
,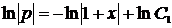 ,
, ,
, ,
, ,
, ,
, ,
, .
. .
. – уравнение Бернулли,
– уравнение Бернулли, ,
, ,
,

 ,
, ,
,  ,
,  ,
,  ,
,  ,
, 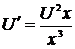 ,
,
 ,
, 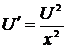 ,
, ,
,  ,
, ,
,  ,
,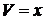 .
.  ,
, ,
, ,
, ,
, ,
, .
.
 , то общее решение уравнения Бернулли будет иметь вид
, то общее решение уравнения Бернулли будет иметь вид  или
или  .
. и получим
и получим  , откуда
, откуда  . Найдём этот интеграл отдельно.
. Найдём этот интеграл отдельно.



 ) решаются с помощью замены
) решаются с помощью замены  новая неизвестная функция. Тогда
новая неизвестная функция. Тогда  . Исходное уравнение примет вид
. Исходное уравнение примет вид  дифференциальное уравнение первого порядка.
дифференциальное уравнение первого порядка.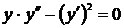 ,
,  .
. ,
,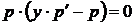 ,
, , или
, или  ,
, 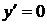 ,
, 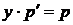 ,
,  ,
,  ,
, .
. 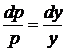 ,
,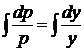 ,
, ,
, ,
,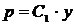 ,
, .
. . Подставим в уравнение
. Подставим в уравнение  ,
,  и получим
и получим  , откуда
, откуда  .
. .
. ,
, ,
, ,
,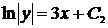 ,
, .
.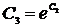 и получим
и получим  .
. (или
(или  при
при  ), то есть получим равенство
), то есть получим равенство  , откуда найдём
, откуда найдём  .
. .
.