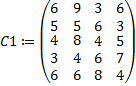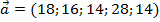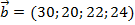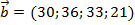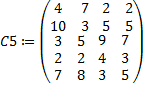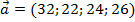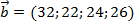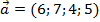Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Правила выполнения и оформления контрольный работ⇐ ПредыдущаяСтр 11 из 11 1. Контрольная работа должна быть выполнена в отельной тетради в клетку. Необходимо оставить поля для замечаний рецензента. 2. На обложке тетради должны быть четко написаны фамилия и инициалы студента, его учебный шифр, название дисциплины, номер контрольной работы, номер варианта. 3. В работу должны быть включены все задачи, указанные в контрольных заданиях, строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются. 4. Задачи и их решения следуют располагать в порядке возрастания номеров, указанных в контрольных заданиях, сохраняя номера задач. 5. Перед решением каждой задачи необходимо полностью записать ее условие. 6. Решение задач должны быть изложены подробно и аккуратно, объясняя все действия по ходу решения. 7. После получения прорецензированной работы студент должен исправить все ошибки, недочеты, замечания и выполнить рекомендации рецензента.
При выполнении контрольной работы необходимо строго придерживаться указанных выше правил. Работы, выполненные без соблюдения этих правил, не зачитываются.
1. ЗАДАЧА ОБ ОПТИМАЛЬНОМ РАСПРЕДЕЛЕНИИ ПРОИЗВОДИТЕЛЬНЫХ РЕСУРСОВ.
УСЛОВИЕ ЗАДАЧИ Есть три вида станков: А1, А2, А3. На этих станках последовательно обрабатываются детали трех видов: В1, В2, В3. Известно сколько часов каждая деталь изготавливается на каждом станке.ю сколько может проработать каждый станок и какая прибыль может быть получена при продаже одной детали каждого типа. Данные приведены в таблице. Требуется найти оптимальный план работы станков, т.е. установить, сколько деталей и каких видов надо выпустить, чтобы получить максимальную прибыль.  Задание 1.Построить математическую модель задачи; привести математическую модель задачи к каноническому виду; найти начальный опорный план задачи; решить задачу симплекс методом; дать экономическую интерпретацию полученных результатов.
Задача 1.1
Задача 1.2
Задача 1.3
Задача 1.4
Задача 1.5
Задача 1.6
Задача 1.7
Задача 1.8
Задача 1.9
Задача 1.10
Задача о смесях Условие задачи Из двух видов сырья необходимо составить смесь, в состав которой должно входить не менее указанных единиц химического вещества В1, В2, В3 соответственно. Цена 1 кг сырья каждого вида, а также количество единиц химического вещества, содержащегося в 1 кг сырья каждого вида, указаны в таблице. Составить смесь, имеющую минимальную стоимость. Задание 2:Построить математическую модель задачи; решить задачу графическим способом; симплекс методом; дать экономическую интерпретацию полученных результатов.
Задача 2.1
Задача 2.2
Задача 2.3
Задача 2.4
Задача 2.5
Задача 2.6
Задача 2.7
Задача 2.8
Задача 2.9
Задача 2.10
Транспортная задача Условие задачи Товары с
Задание 3. Составить математическую модель задачи; привести ее к стандартной транспортной задаче (с балансом); построить начальный опорный план задачи; решить задачу (методом потенциалов).
Вариант 1
Необходимо полностью удовлетворить потребности первого магазина
Вариант2
Необходимо полностью освободить третью базу
Вариант 3
Необходимо полностью освободить первую базу
Вариант 4
Необходимо полностью удовлетворить потребности четвертого магазина
Вариант5
Необходимо полностью освободить первую базу
Вариант 6
Необходимо полностью освободить вторую базу Вариант 7
Необходимо полностью удовлетворить потребности третьего магазина
Вариант 8
Необходимо полностью удовлетворить потребности третьего магазина
Вариант 9
Необходимо полностью освободить третью базу
Вариант 10
Необходимо полностью освободить четвертую базу
Заключение В представленной работе рассмотрен ряд задач оптимального управления как с точки зрения теории, так и с точки зрения практического их решения. При этом особое внимание уделено усвоению и закреплению студентами практических навыков по решению данного типа задач, а также пониманию их экономического смысла в практических условиях хозяйствования. Изложение представленного материала не перегружено математическими конструкциями, выходящими за рамками математики для инженерных и экономических специальностей высших учебных заведений. Следует отметить, что для более глубокого изучения вопросов, рассматриваемых в данной работе необходимо обратиться к списку литературы, в которой включены работы, ставшие классическими.
Список используемой литературы
1. 1. Ашманов, С.А. Линейное программирование / С.А.Ашманов. – М.: Наука, 1981. – 304 с.
2. Вентцель, Е.С. Исследование операций: Задачи, принципы, методология / Е.С.Вентцель. – М.: Высшая школа, 2001. – 208 с.
3. Гольдштейн, Е.Г. Линейное программирование: Теория, методы и приложения / Е.Г.Гольдштейн, Д.Б.Юдин. – М.: Наука, 1969. – 736 с.
4. Кофман, А. Методы и модели исследования операций / А.Кофман. – М.: Мир, 1966. – 523 с.
5. Силич, В.А. Системный анализ и исследование операций: учебное пособие / В.А. Силич, М.П. Силич. – Томск: Изд-во ТПУ, 2000. – 96 с.
6. Хэмди, А. Таха. Введение в исследование операций. пер. с англ. / А. Таха Хэмди. – М.: Издательский дом «Вильямс», 2007. – 912 с.
7. Дякин, В.Н. Оптимизация управления промышленным предприятием / В.Н. Дякин, В.Г. Матвейкин, Б.С. Дмитриевский. – Тамбов : Изд-во Тамб. гос. техн. ун-та, 2004. – 84 с.
8. Акулич, И.Л. Математическое программировани в примерах и задачах: учебное пособие для студентов эконом. с спец. Вузов / И.Л. Акулич. – Мн. : Высшая школа, 1986.
9. Большакова, И.В. Линейное программирование : учебно-метод. Пособие к контрольной работе для студ. эконом. факультета / И.В. Большакова. – МН. : БНТУ, 2004.
10. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. - М.: Высшая школа, 1980.
11. Калихман И.Л. Линейная алгебра и программирование. - М.: Высшая школа, 1967.
12. Нит И.В. Линейное программирование. - М.: Изд-во МГУ, 1978.
13. Юдин Д.Б., Гольштейн Е.Г. Линейное программирование. Теория и конечные методы. - М.: Физматиз, 1963.
14. Тарасенко Н.В. Математика-2. Линейное программирование: курс лекций. - Иркутск: изд-во БГУЭП, 2003.
15. Математическое программирование в примерах и задачах: Учеб. пособие. - 2-е изд., испр. и доп. - М.: Высш. шк., 1993. - 336 с.
16. www.yandex.ru
17. www.mathematica.ru <http://www.mathematica.ru>
18. www.monax.ru
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 352. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 баз поставляются с
баз поставляются с  магазинов. Потребности магазинов в товарах равны
магазинов. Потребности магазинов в товарах равны  тыс. ед.
тыс. ед.  . Запасы товаров на базах составляют
. Запасы товаров на базах составляют  тыс. ед.,
тыс. ед., 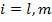 . Затраты на перевозку 1 тыс. ед. в ден. ед. представлены матрицей затрат
. Затраты на перевозку 1 тыс. ед. в ден. ед. представлены матрицей затрат  . Запланировать перевозку с минимальными затратами при заданном дополнительном условии.
. Запланировать перевозку с минимальными затратами при заданном дополнительном условии.