
Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Основные виды экономических задач, сводящихся к ЗЛП
Задача о наилучшем использовании ресурсов. Пусть некоторая производственная единица (цех, завод, объединение и т. д.), исходя из конъюнктуры рынка, технических или технологических возможностей и имеющихся ресурсов, может выпускать n различных видов продукции (товаров), известных под номерами, обозначаемыми индексом j  . Будем обозначать эту продукцию . Будем обозначать эту продукцию  . Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т. д.). Все эти виды ограничивающих факторов называют ингредиентами . Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т. д.). Все эти виды ограничивающих факторов называют ингредиентами  . Пусть их число равно . Пусть их число равно  ; припишем им индекс i ; припишем им индекс i  . Они ограничены, и их количества равны соответственно . Они ограничены, и их количества равны соответственно  условных единиц. Таким образом, условных единиц. Таким образом,  - вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т. д. Примем в качестве такой меры, например, цену реализации - вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т. д. Примем в качестве такой меры, например, цену реализации
  , т.е. , т.е.  — вектор цен. Известны также технологические коэффициенты — вектор цен. Известны также технологические коэффициенты  , которые указывают, сколько единиц i–го ресурса требуется для производства единицы продукции >j-го вида. Матрицу коэффициентов , которые указывают, сколько единиц i–го ресурса требуется для производства единицы продукции >j-го вида. Матрицу коэффициентов  называют технологической и обозначают буквой А. Имеем называют технологической и обозначают буквой А. Имеем  . Обозначим через . Обозначим через  план производства, показывающий, какие виды товаров план производства, показывающий, какие виды товаров 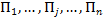 нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах. нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.
Так как 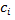 - цена реализации единицы j-й продукции, цена реализованных - цена реализации единицы j-й продукции, цена реализованных  единиц будет равна единиц будет равна  , а общий объем реализации , а общий объем реализации  . .
Это выражение — целевая функция, которую нужно максимизировать.
Так как  - расход i-го ресурса на производство - расход i-го ресурса на производство  единиц j-й продукции, то, просуммировав расход i-горесурса на выпуск всех n видов продукции, получим общий расход этого ресурса, который не должен превосходить единиц j-й продукции, то, просуммировав расход i-горесурса на выпуск всех n видов продукции, получим общий расход этого ресурса, который не должен превосходить  единиц: единиц:
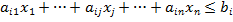
Чтобы искомый план  был реализован, наряду с ограничениями на ресурсы нужно наложить условие неотрицательности на объёмы был реализован, наряду с ограничениями на ресурсы нужно наложить условие неотрицательности на объёмы  выпуска продукции: выпуска продукции: 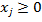  . .
Таким образом, модель задачи о наилучшем использовании ресурсов примет вид:
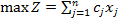 (1.33) (1.33)
при ограничениях:
 (1.34) (1.34)
 (1.35) (1.35)
Так как переменные  входят в функцию входят в функцию 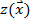 и систему ограничений только в первой степени, а показатели и систему ограничений только в первой степени, а показатели  являются постоянными в планируемый период, то (1.33)-(1.35) – задача линейного программирования. являются постоянными в планируемый период, то (1.33)-(1.35) – задача линейного программирования.
Задача о смесях
В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходных материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе задач относятся задачи о выборе диеты, составлении кормового рациона в животноводстве, шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности, смесей для получения бетона в строительстве и т. д. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигает на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы.
Пример. Для откорма животных используется три вида комбикорма: А, В и С. Каждому животному в сутки требуется не менее 800 г. жиров, 700 г. белков и 900 г. углеводов. Содержание в 1 кг. каждого вида комбикорма жиров белков и углеводов (граммы) приведено в таблице:
| Содержание в 1 кг.
| Комбикорм
|
|
| А
| В
| С
| | Жиры
| 320
| 240
| 300
| | Белки
| 170
| 130
| 110
| | Углеводы
| 380
| 440
| 450
| | Стоимость 1 кг
| 31
| 23
| 20
|
Сколько килограммов каждого вида комбикорма нужно каждому животному, чтобы полученная смесь имела минимальную стоимость?
Математическая модель задачи есть:
 - количество комбикорма А,В и С. Стоимость смеси есть: - количество комбикорма А,В и С. Стоимость смеси есть:

Ограничения на количество ингредиентов:
  ; ;
Задача о раскрое материалов
Сущность задачи об оптимальном раскрое состоит в разработке таких технологически допустимых планов раскроя, при которых получается необходимый комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) сводятся к минимуму. Рассматривается простейшая модель раскроя по одному измерению. Более сложные постановки ведут к задачам целочисленного программирования.
Задача о назначениях
Речь идет о задаче распределения заказа (загрузки взаимозаменяемых групп оборудования) между предприятиями (цехами, станками, исполнителями) с различными производственными и технологическими характеристиками, но взаимозаменяемыми в смысле выполнения заказа. Требуется составить план размещения заказа (загрузки оборудования), при котором с имеющимися производственными возможностями заказ был бы выполнен, а показатель эффективности достигал экстремального значения.
Пример. Цеху металлообработки нужно выполнить срочный заказ на производство деталей. Каждая деталь обрабатывается на 4-х станках С1, С2, С3 и С4. На каждом станке может работать любой из четырех рабочих Р1, Р2, Р3, Р4, однако, каждый из них имеет на каждом станке различный процент брака. Из документации ОТК имеются данные о проценте брака каждого рабочего на каждом станке:
|
| С1
| С2
| С3
| С4
| | Р1
| 2,3
| 1,9
| 2,2
| 2,7
| | Р2
| 1,8
| 2,2
| 2,0
| 1,8
| | Р3
| 2,5
| 2,0
| 2,2
| 3,0
| | Р4
| 2,0
| 2,4
| 2,4
| 2,8
|
Необходимо так распределить рабочих по станкам, чтобы суммарный процент брака (который равен сумме процентов брака всех 4-х рабочих) был минимален. Чему равен этот процент?
Обозначим за  - переменные, которые принимают значения 1, если i-й рабочий работает на j-м станке. Если данное условие не выполняется, то - переменные, которые принимают значения 1, если i-й рабочий работает на j-м станке. Если данное условие не выполняется, то  . Целевая функция есть: . Целевая функция есть:
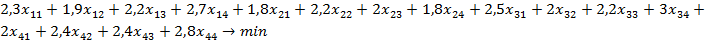 . .
Вводим ограничения. Каждый рабочий может работать только на одном станке, то есть

Кроме того, каждый станок обслуживает только один рабочий:

Кроме того, все переменные должны быть целыми и неотрицательными: 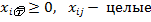 . .
Транспортная задача.
Частным случаем задачи линейного программирования является транспортная задача.
ТЗ в общем виде состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления  в в  пунктов назначения пунктов назначения  n. В качестве критерия оптимальности можно взять минимальную стоимость перевозок всего груза, либо минимальное время его доставки. n. В качестве критерия оптимальности можно взять минимальную стоимость перевозок всего груза, либо минимальное время его доставки.
Рассмотрим задачу с первым критерием, обозначив через сn тарифы перевозок единицы груза из i-го пункта отправления в j-й пункт назначения, через ai - запасы груза в пункте Аi через bj - потребности в грузе пункта  - количество единиц груза, перевозимого из i-го пункта в j-й пункт. - количество единиц груза, перевозимого из i-го пункта в j-й пункт.
Составим математическую модель задачи. Так как от i-гo поставщика к j-му потребителю запланировано к перевозке 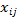 единиц груза. единиц груза.
Таблица 2.1
| Поставщики
| Потребители
| Запасы
| | B1
| B2
| ...
| Bn
| | А1
| C11
X11
| C12
X12
| ...
| C1n
X1n
| a1
| | А2
| C21
X21
| C22
X22
| ...
| C2n
X2n
| a2
| | ...
| ...
| ...
| ...
| ...
| ...
| | Аm
| Cm1
Xm1
| Cm2
Xm2
| ...
| Cmn
Xmn
| am
| | Потребности
| b1
| b2
| ...
| bn
| ∑ai=∑bj
|
Соответственно математическая постановка задачи состоит в определении минимума целевой функции

| (2.11)
| при условиях:
 (2.12) (2.12)
 (2.13) (2.13)
 (2.14) (2.14)
Всякое неотрицательное решение систем уравнений (2.12)-(2.14), определяемое матрицей 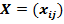 , называют опорным планом ТЗ, а план , называют опорным планом ТЗ, а план 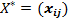 , при котором функция Z принимает минимальное значение - называется оптимальным планом ТЗ. , при котором функция Z принимает минимальное значение - называется оптимальным планом ТЗ.
Все данные, а затем и опорный план, удобно занести в распределительную таблицу.
Если общее количество груза в пунктах отправления и общая потребность в нем в пунктах назначения совпадают, т.е.
 (2.16) (2.16)
то модель ТЗ называется закрытой.
Теорема 4.Любая транспортная задача, у которой суммарный объем запасов совпадает с суммарным объемом потребностей, имеет решение.
Для доказательства теоремы необходимо показать, что хотя бы один план задачи и линейная функция на множестве планов при заданных условиях существу ограничена.
Доказательство:
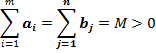
Тогда величины  являются планом, так как они удовлетворяют, системе ограничений (2.12), (2.13). Действительно, подставляя значения являются планом, так как они удовлетворяют, системе ограничений (2.12), (2.13). Действительно, подставляя значения 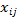 в (2.12) и (2.13), имеем в (2.12) и (2.13), имеем
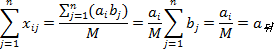
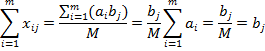
Выберем из значений 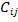 наибольшее наибольшее  и заменим в линейной функции (2.11) все коэффициенты на и заменим в линейной функции (2.11) все коэффициенты на  тогда, учитывая (2.12), получаем тогда, учитывая (2.12), получаем
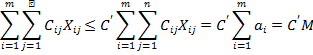
Выберем из значений  наименьшее наименьшее  и заменим в линейной функции все коэффициенты на и заменим в линейной функции все коэффициенты на  тогда, имеем тогда, имеем 
Объединяя два последних неравенства в одно двойное, окончательно получаем  , т. е. линейная функция ограничена на множестве планов транспортной задачи. , т. е. линейная функция ограничена на множестве планов транспортной задачи.
Ч.Т.Д.
Если общее количество груза в пунктах отправления и общая потребность в нем в пунктах назначения не совпадают ТЗ называется открытой. Введением фиктивного потребителя (если  ), или фиктивного отправителя (если ), или фиктивного отправителя (если  ), любая задача приводится к закрытой модели (во всех фиктивных ячейках таблицы полагают ), любая задача приводится к закрытой модели (во всех фиктивных ячейках таблицы полагают  ). Для разрешимости задачи равенство (2.15) является необходимым и достаточным условием. ). Для разрешимости задачи равенство (2.15) является необходимым и достаточным условием.
Нахождение опорных и оптимального планов ТЗ можно вести симплексным методом, но, ввиду специфики ТЗ, и большого ее прикладного значения, разработаны специальные методы.
Нахождение опорных планов ТЗ можно осуществить одним из пяти методов: северо-западного угла, минимальной стоимости, аппроксимации Фогеля, двойного предпочтения и дельта-метода.
Методы составления опорного плана транспортной задачи.
|


 . Будем обозначать эту продукцию
. Будем обозначать эту продукцию  . Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т. д.). Все эти виды ограничивающих факторов называют ингредиентами
. Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т. д.). Все эти виды ограничивающих факторов называют ингредиентами  . Пусть их число равно
. Пусть их число равно  ; припишем им индекс i
; припишем им индекс i  . Они ограничены, и их количества равны соответственно
. Они ограничены, и их количества равны соответственно  условных единиц. Таким образом,
условных единиц. Таким образом,  - вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т. д. Примем в качестве такой меры, например, цену реализации
- вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т. д. Примем в качестве такой меры, например, цену реализации
 , т.е.
, т.е.  — вектор цен. Известны также технологические коэффициенты
— вектор цен. Известны также технологические коэффициенты  , которые указывают, сколько единиц i–го ресурса требуется для производства единицы продукции >j-го вида. Матрицу коэффициентов
, которые указывают, сколько единиц i–го ресурса требуется для производства единицы продукции >j-го вида. Матрицу коэффициентов  . Обозначим через
. Обозначим через  план производства, показывающий, какие виды товаров
план производства, показывающий, какие виды товаров 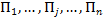 нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.
нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.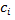 - цена реализации единицы j-й продукции, цена реализованных
- цена реализации единицы j-й продукции, цена реализованных  единиц будет равна
единиц будет равна  , а общий объем реализации
, а общий объем реализации  .
. - расход i-го ресурса на производство
- расход i-го ресурса на производство  единиц:
единиц: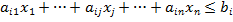
 был реализован, наряду с ограничениями на ресурсы нужно наложить условие неотрицательности на объёмы
был реализован, наряду с ограничениями на ресурсы нужно наложить условие неотрицательности на объёмы 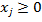
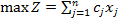 (1.33)
(1.33) (1.34)
(1.34) (1.35)
(1.35) входят в функцию
входят в функцию 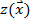 и систему ограничений только в первой степени, а показатели
и систему ограничений только в первой степени, а показатели  являются постоянными в планируемый период, то (1.33)-(1.35) – задача линейного программирования.
являются постоянными в планируемый период, то (1.33)-(1.35) – задача линейного программирования. - количество комбикорма А,В и С. Стоимость смеси есть:
- количество комбикорма А,В и С. Стоимость смеси есть:

 ;
; - переменные, которые принимают значения 1, если i-й рабочий работает на j-м станке. Если данное условие не выполняется, то
- переменные, которые принимают значения 1, если i-й рабочий работает на j-м станке. Если данное условие не выполняется, то  . Целевая функция есть:
. Целевая функция есть: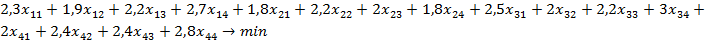 .
.

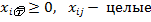 .
. в
в  пунктов назначения
пунктов назначения  n. В качестве критерия оптимальности можно взять минимальную стоимость перевозок всего груза, либо минимальное время его доставки.
n. В качестве критерия оптимальности можно взять минимальную стоимость перевозок всего груза, либо минимальное время его доставки.  - количество единиц груза, перевозимого из i-го пункта в j-й пункт.
- количество единиц груза, перевозимого из i-го пункта в j-й пункт. 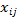 единиц груза.
единиц груза.
 (2.12)
(2.12) (2.13)
(2.13) (2.14)
(2.14)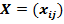 , называют опорным планом ТЗ, а план
, называют опорным планом ТЗ, а план 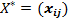 , при котором функция Z принимает минимальное значение - называется оптимальным планом ТЗ.
, при котором функция Z принимает минимальное значение - называется оптимальным планом ТЗ.  (2.16)
(2.16)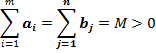
 являются планом, так как они удовлетворяют, системе ограничений (2.12), (2.13). Действительно, подставляя значения
являются планом, так как они удовлетворяют, системе ограничений (2.12), (2.13). Действительно, подставляя значения 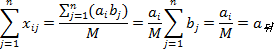
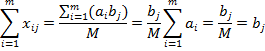
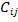 наибольшее
наибольшее  и заменим в линейной функции (2.11) все коэффициенты на
и заменим в линейной функции (2.11) все коэффициенты на  тогда, учитывая (2.12), получаем
тогда, учитывая (2.12), получаем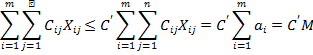
 наименьшее
наименьшее  и заменим в линейной функции все коэффициенты на
и заменим в линейной функции все коэффициенты на  тогда, имеем
тогда, имеем 
 , т. е. линейная функция ограничена на множестве планов транспортной задачи.
, т. е. линейная функция ограничена на множестве планов транспортной задачи.  ), или фиктивного отправителя (если
), или фиктивного отправителя (если  ), любая задача приводится к закрытой модели (во всех фиктивных ячейках таблицы полагают
), любая задача приводится к закрытой модели (во всех фиктивных ячейках таблицы полагают  ). Для разрешимости задачи равенство (2.15) является необходимым и достаточным условием.
). Для разрешимости задачи равенство (2.15) является необходимым и достаточным условием.