
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод двойного предпочтенияЕсли таблица стоимостей велика, то перебор всех элементов затруднителен. В этом случае используют метод двойного предпочтения, суть которого заключается в следующем.
Пример 3
Применим метод двойного предпочтения к задаче, условия которой записаны в табл. 2.7. Таблица 2.7
Сначала, отмечаем знаком V ячейку с наименьшей стоимостью в каждом столбце, затем - в каждой строке (табл. 2.8). Таблица 2.8
Ячейки  Таблица 2.9
Вычислим общую сумму затрат на перевозку груза по этому плану: Таким образом, наименьшую стоимость имеет опорный план, полученный методом двойного предпочтения, следовательно, он наиболее близок к оптимальному плану.
Оптимальность плана транспортной задачи. Метод потенциалов Пусть одним из рассмотренных в п.2.6 методов найден опорный план, содержащий Вопрос об оптимальности опорного плана решает следующая теорема: Теорема 5. Если для некоторого плана 1. то план Отметим, что система (2.16) Для «улучшения» опорного плана (при невыполнении условия (2.17)) выбирают свободную клетку с Циклом называют замкнутую ломаную линию, все вершины которой лежат в занятых ячейках, кроме одной, расположенной в свободной клетке, подлежащей заполнению, а звенья параллельны строкам и столбцам, причем в каждой строке (столбце) лежит не более 2-х вершин. Всем вершинам поочередно приписывают знаки «+» и «-», начиная со свободной клетки.
Пример 1 Проверить оптимальность опорного плана ТЗ, решенной, в примере 6.
Проверив свободные клетки, находим, что лишь в клетке
Таблица 2.10
при этом будет В системе потенциалов для этого плана лишь 1-ое уравнение заменялся равенством
Свойство 1. Если, для некоторого оптимального плана
Пример 2.
Проверить оптимальность ТЗ, определенную таблицей (табл.2.11). Таблица 2.11
Решение. Ведем построение опорного плана методом наименьшей стоимости (таблица 2.12) Таблица 2.12
Замечаем, что в результате пересчета по циклу оказалось, что число занятых клеток меньше, чем Получаем опорный план:
Вычислим общую сумму затрат на перевозку груза по этому плану: Составляем систему уравнений потенциалов: Полагая
Проверив свободные клетки, убеждаемся, что по теореме 5 план оптимален, следовательно,
Свойство 2. Любая выпуклая линейная комбинация двух оптимальных планов также является оптимальным планом.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1310. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


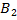








 имеют отметку
имеют отметку  , следовательно, с них и начинаем заполнение. Затем заполняем ячейку
, следовательно, с них и начинаем заполнение. Затем заполняем ячейку 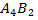 (т.к. в столбце
(т.к. в столбце  нет ни одной ячейки с отметкой
нет ни одной ячейки с отметкой  . План, полученный в табл. 2.9, является вырожденным опорным планом.
. План, полученный в табл. 2.9, является вырожденным опорным планом.
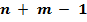 занятых клеток (в некоторых из них могут стоять нули). Поставим в соответствие каждому пункту отправления
занятых клеток (в некоторых из них могут стоять нули). Поставим в соответствие каждому пункту отправления  некоторое число
некоторое число 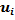
 и каждому пункту назначения
и каждому пункту назначения  - число
- число  . Эти числа назовем потенциалами, соответственно, пунктов отправления и пунктов назначения.
. Эти числа назовем потенциалами, соответственно, пунктов отправления и пунктов назначения. ) транспортной задачи выполняются условия:
) транспортной задачи выполняются условия: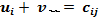 для
для  (для занятых клеток), (2.16)
(для занятых клеток), (2.16) для
для  (для свободных клеток), (2.17)
(для свободных клеток), (2.17) является оптимальным. Из теоремы следует, что если для некоторой свободной клетки
является оптимальным. Из теоремы следует, что если для некоторой свободной клетки  , то план не является оптимальным.
, то план не является оптимальным. уравнений содержит
уравнений содержит  неизвестных
неизвестных  , и потому, приравнивая одно из них, например
, и потому, приравнивая одно из них, например  к нулю, однозначно определим остальные неизвестные.
к нулю, однозначно определим остальные неизвестные. и строят для нее цикл пересчета (сдвига).
и строят для нее цикл пересчета (сдвига). , где
, где  - сумма тарифов в положительных вершинах,
- сумма тарифов в положительных вершинах,  - в отрицательных вершинах цикла.
- в отрицательных вершинах цикла.  (план называется вырожденным). В этом случае следует заполнить числом «0» пустую клетку, имеющую минимальный тариф, и не образующую с занятыми клетками замкнутого прямоугольного контура.
(план называется вырожденным). В этом случае следует заполнить числом «0» пустую клетку, имеющую минимальный тариф, и не образующую с занятыми клетками замкнутого прямоугольного контура.





 будет
будет  .
.  дает новый опорный план
дает новый опорный план

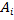


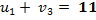 .
.  , находим
, находим 
 и
и 
 транспортной задачи, выполняется условие:
транспортной задачи, выполняется условие:  для
для  (для свободных клеток), то, существует как минимум еще один оптимальный план, для которого общая стоимость плана перевозок остается прежней, поскольку
(для свободных клеток), то, существует как минимум еще один оптимальный план, для которого общая стоимость плана перевозок остается прежней, поскольку 
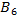
 , т.е. получен вырожденный план. Следовательно, заполняем числом «0» пустую клетку
, т.е. получен вырожденный план. Следовательно, заполняем числом «0» пустую клетку  , т.к. она имеет минимальный тариф
, т.к. она имеет минимальный тариф  , и не образует с занятыми клетками замкнутого прямоугольного контура.
, и не образует с занятыми клетками замкнутого прямоугольного контура.









 .
. 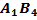 сумма потенциалов равна стоимости перевозки
сумма потенциалов равна стоимости перевозки  и в нее по циклу, можно переместить 10 ед. груза.
и в нее по циклу, можно переместить 10 ед. груза.