
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Открытые модели ТЗ и усложнения в ее постановке.
Транспортная задача, в которой суммарные запасы и потребности совпадают, т. е. выполняется условие Открытая модель ТЗ решается приведением к закрытой модели. В случае (а), когда суммарные запасы превышают суммарные потребности, т.е. Стоимость перевозки единицы груза, как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится. Замечание 1. Прежде чем решать какую-нибудь транспортную задачу, необходимо сначала проверять, к какой модели она принадлежит, и только после этого непосредственно составлять распределительную таблицу. Замечание 2.При составлении первоначального опорного плана методом минимальной стоимости или двойного предпочтения необходимо наименьшую стоимость выбирать только среди стоимостей реальных поставщиков и потребителей, а запасы фиктивного поставщика (потребности фиктивного потребителя) распределять в последнюю очередь. Это позволит получить план, более близкий к оптимальному.  Пример 1
Составить план перевозок грузов с наименьшей общей стоимостью от четырех поставщиков
Решение Вычислим суммарные запасы и потребности. Соответственно: Таблица 2.13
Получаем опорный план
проверяем его на оптимальность, для чего составляем систему уравнений потенциалов:
Проверив свободные клетки, находим, что получен оптимальный план.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 330. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 называется закрытой моделью; в противном случае – открытой. Для открытой модели может быть два случая:
называется закрытой моделью; в противном случае – открытой. Для открытой модели может быть два случая: 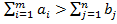 ;
;  .
.  ), потребности которого
), потребности которого  . В случае (б), когда суммарные потребности превышают суммарные запасы, т.е.
. В случае (б), когда суммарные потребности превышают суммарные запасы, т.е.  ), запасы которого
), запасы которого  .
. ), соответственно, в количествах
), соответственно, в количествах  . К пяти потребителям
. К пяти потребителям  соответственно, в количествах
соответственно, в количествах 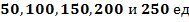 .. Стоимости перевозок единицы груза из каждого пункта отправления в каждый пункт назначения являются известными величинами и задаются матрицей
.. Стоимости перевозок единицы груза из каждого пункта отправления в каждый пункт назначения являются известными величинами и задаются матрицей
 . Потребности превышают запасы на
. Потребности превышают запасы на  . Необходимо ввести фиктивного поставщика (строка
. Необходимо ввести фиктивного поставщика (строка  Получим закрытую модель ТЗ. Заполняем распределительную таблицу (табл. 2.13) методом минимальной стоимости.
Получим закрытую модель ТЗ. Заполняем распределительную таблицу (табл. 2.13) методом минимальной стоимости.
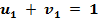 ,
,
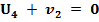 ,
,
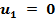 ,, найдём:
,, найдём:

 ,
,
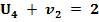 ,
,
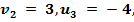
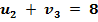 ,
,

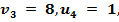
 ,
,


 ,
,

 , получает
, получает