
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Постановка задачи линейного программирования и свойства ее решенийСтр 1 из 11Следующая ⇒ Общие методические указания Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение теоритического материала по учебникам, решение задач выполнение контрольных работ. В помощь студентам университет организуется чтение лекций и проведение практических занятий. Заверщающим этапом изучения курса прикладной математики является сдача экзамена в соответсвии с учебным планом.
Вопросы для подготовки к экзамену по курсу прикладной математики, изучаемые по программе в третьем семестре.
1. Постановка задачи линейного программирования (ЛП). Геометрическая интерпретация решения. Классическая форма записи задачи линейного программирования (ЛП). Базис опорного плана. Базисные переменные. 2. Симплекс-метод. Идея симплекс-метода. Формулы и условия перехода. Признаки прекращения счета. Табличный симплекс-метод. Формирование опорного базисного решения. Симплекс-таблица. Пересчет элементов таблицы. Отыскание решения. 3. Двойственная задача ЛП. Структура и свойства двойственной задачи. Транспортная задача ЛП. 4. Опорные планы транспортной задачи. Методы нахождения опорных планов. Решение транспортной задачи. Метод потенциалов. 5. Постановка задачинелинейного программирования. Оптимизация без ограничений (классические методы поиска экстремума функции одной и нескольких переменных; градиентные методы поиска экстремума). 6. Оптимизация при наличии ограничений (общая теория оптимизации при ограничениях типа равенств и типа неравенств). 7. Задача о кратчайшем пути.  8. Задача коммивояжера 9. Предмет и задачи теории игр. Стратегические конечные матричные игры двух лиц с нулевой суммой. Преобразование матричных игр. Игры с седловой точкой. Понятие чистых стратегий. 10. Игры без седловой точки. Понятие смешанных стратегий. Метод решения конечных матричных игр с помощью линейного программирования 11. Временные ряды. Стационарные ряды. Белый шум. Автокорреляции и автоковариация 12. Детерминированные временные ряды. Виды трендов. 13. Разделение трендов и шума методами регрессионного анализа 14. Качество регрессионной модели. Сопоставление моделей через остаточную дисперсию. Критерий Фишера 15. Однофакторный дисперсионный анализ 16. Принципы распознавания образа 17. Модель авторегрессии, Марковский процесс 18. Модель авторегрессии, процесс Юла 19. Критерии случайности. Метод поворотных точек 20. Критерии случайности. Критерий Кэндела 21. Прогнозирование с учетом тренда и авторегрессии 22. Эргодические временные ряды. Определение автокорреляции по одной реализации.
Методы линейного программирования. Многие задачи, с которыми приходится иметь дело в повседневной практике, являются многовариантными. Среди множества возможных вариантов в условиях рыночных отношений приходится отыскивать наилучшие в некотором смысле при ограничениях, налагаемых на природные, экономические и технологические возможности. В связи с этим возникла необходимость применять для анализа и синтеза экономических ситуаций и систем математические методы и современную вычислительную технику? Такие методы объединяются под общим названием — математическое программирование. Основные понятия Математическое программирование — область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.
Постановка задачи линейного программирования и свойства ее решений Линейное программирование — раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.
при ограничениях
где
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 316. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6)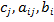 - заданные действительные числа; (1.1) – целевая функция; (1.1) – (1.6) –ограничения; -
- заданные действительные числа; (1.1) – целевая функция; (1.1) – (1.6) –ограничения; - 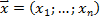 план задачи.
план задачи. (1.7)
(1.7)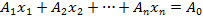 (1.8)
(1.8) (1.9)
(1.9) вообще невозможен. При
вообще невозможен. При  система имеет единственное решение, которое будет при
система имеет единственное решение, которое будет при  оптимальным. В этом случае проблема выбора оптимального решения теряет смысл. Выясним структуру координат угловой точки многогранных решений. Пусть
оптимальным. В этом случае проблема выбора оптимального решения теряет смысл. Выясним структуру координат угловой точки многогранных решений. Пусть  . В этом случае система векторов
. В этом случае система векторов  содержит базис — максимальную линейно независимую подсистему векторов, через которую любой вектор системы может быть выражен как ее линейная комбинация. Базисов, вообще говоря, может быть несколько, но не более
содержит базис — максимальную линейно независимую подсистему векторов, через которую любой вектор системы может быть выражен как ее линейная комбинация. Базисов, вообще говоря, может быть несколько, но не более  . Каждый из них состоит точно из r векторов. Переменные ЗЛП, соответствующие r векторам базиса, называют, как известно, базисными и обозначают БП. Остальные
. Каждый из них состоит точно из r векторов. Переменные ЗЛП, соответствующие r векторам базиса, называют, как известно, базисными и обозначают БП. Остальные  переменных будут свободными, их обозначают СП. Не ограничивая общности, будем считать, что базис составляют первые m векторов
переменных будут свободными, их обозначают СП. Не ограничивая общности, будем считать, что базис составляют первые m векторов  . Этому базису соответствуют базисные переменные
. Этому базису соответствуют базисные переменные  , а свободными будут переменные
, а свободными будут переменные 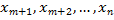 .
. (1. 10)
(1. 10)