
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Критерий обобщенного максимина(пессимизма-оптимизма) Гурвица при выборе решения вместо двух крайностей в оценке ситуации можно придерживаться некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего, благоприятного поведения природы. Для каждого решения необходимо определить линейную комбинацию min и max выигрыша и взять ту стратегию, для которой эта величина окажется наибольшей. Оценочная функция критерия (HW) находится между точками предельного оптимизма и крайнего пессимизма. Оценочная функция имеет две формы записи:
где k — «степень пессимизма» («коэффициент пессимизма», весовой множитель), 0£k£1.При k=1 критерий Гурвица совпадает с критерием Вальда(ZMM) - ориентация на осторожное поведение. При k=0 – ориентация на предельный риск (больший выигрыш, сопряжен с большим риском). Значение между 0 и 1 выбираются в зависимости от конкретной обстановки и склонности к риску лица, принимающего решение. Часто весовой множитель принимают в качестве некоторой "средней" точки зрения(k=0,5). Пример.Определить оптимальные варианты из множества решений, заданных матрицей решений с использованием критерия Гурвица ZHW. При решении задачи учесть, что степень доверия к позиции крайней осторожности ZMM должна быть не более 0,3
Матрица решений дополняется столбцом, содержащим средние взвешенные наименьшего и наибольшего результатов каждой строки. Выбираются те вариантыXi, в строках которых стоят наибольшие элементы eirэтого столбца. По условию  ZAG Критерий Гурвица ZHW можно представить в виде: ZHW=ZMM+ZAG, а в этой задаче с коэффициентами ZHW=kZMM+(1-k)ZAG Решение (считается построчно): а) Минимальный (min) элемент строки умножается на 0.3 а максимальный элемент строки умножается на 0.7 б) Результаты умножений складываются и записываются в дополнительный столбец e1r=(-3)*0.3+7*0.7=4 e2r= e3r= e4r= в) Выбирается максимальное значение дополнительного столбца (max) . Ответ: Задача 6.1:Предприятие готовится к переходу на новые виды продукции, при этом возможные четыре решения Р1, Р2, Р3, Р4, каждому из которых соответствует определенный виды выпуска или их сочетание. Результаты принятых решений существенно зависят от обстановки, которая в значительной мере не определена. Варианты обстановки характеризует структура спроса на новую продукцию, которая может быть трех типов: О1, О2, О3. Выигрыш, характеризующий относительную величину результата (доходы, прибыль и т.п.), соответствующий каждой паре сочетаний решений Р и обстановки О, представлен в таблице 6.1. Таблица 6.1 – Эффективность выпуска новых видов продукции
Необходимо определить такое решение Р, которое по сравнению с другими является наиболее выгодным. Для решения применить критерии Лапласа, Байеса-Лапласа (при q1=0,3; q2=0,3; q3=0,2; q4=0,1; q5=0,1), Вальда, Сэвиджа и Гурвица. Алгоритм решения: 1) рассчитать потери (Hij) для всех решений при всех вариантах обстановки (таблица 6.2). Потери, соответствующие каждой паре сочетаний решений Рi и обстановки Оj, определяются как разность между максимальным выигрышем и выигрышем по конкретному решению при данной обстановке. Таблица 6.2 – Величины потерь при выпуске новых видов продукции
2) Используя критерий Лапласа определить наилучший вариант решения(исходные данные в таблице 6.2). Таблица 6.3 – Величины потерь при выпуске новых видов продукции
Ответ: решение _____
3) Используя критерий Байеса-Лапласа определить наилучший вариант решения (исходные данные в таблице 6.2),приq1=0,5; q2=0,3; q3=0,2. Таблица 6.4 – Величины потерь при выпуске новых видов продукции
Ответ: решение ____
4) Используя критерий Вальда определить наилучший вариант решения(исходные данные в таблице 6.1). Таблица 6.5 – Эффективность выпуска новых видов продукции
Ответ: _________
5)Используя критерий Сэвиджа определить наилучший вариант решения(исходные данные в таблице 6.2). Таблица 6.3 – Величины потерь при выпуске новых видов продукции
Ответ: минимальными из максимальных потерь составляют ____, следовательно, предпочтение необходимо отдавать решению _______, обеспечивающему эти потери. 6) Используя критерий Гурвица определить наилучший вариант решения при (при k=0.5)(исходные данные в таблице 6.2). Задача 6.2.[5] Владелец небольшой кондитерской в начале каждого дня закупает для реализации пирожные, спрос за день данного продукта может быть равен 1,2,3,4 штуки. Стоимость приобретения каждого пирожного - 50 руб., а цена реализации 60 руб. за единицу. Продать невостребованные пирожные на следующий день невозможно, поэтому остаток всегда распродается в конце дня по цене 30 руб. Владельцу кондитерской нужно принять решение и определить, сколько пирожных должно быть закуплено в начале каждого дня.Для решения применить критерии Лапласа, Байеса-Лапласа, Вальда, Сэвиджа и Гурвица (при k=0.4). Решение: а) Определить возможные доходы кондитерской (таблица 6.4) Таблица 6.4 - Возможные доходы кондитерской
Задача 6.3.В приморском городе решено открыть яхт-клуб. Сколько следует закупить яхт (из расчета: одна яхта на 5 человек), если предполагаемое число членов клуба колеблется от 10 до 25 человек (для решения задачи применить критерии Байеса-Лапласа, Лапласа Вальда, Сэвиджа и Гурвица).Годовой абонемент стоит 100 денежных единиц. Цена яхты - 170 денежных единиц. Аренда помещения и хранение яхт обходится в 730 денежных единиц в год Решение. Несомненно, что имеет смысл рассматривать количество приобретаемых яхт в диапазоне от двух до пяти (4 варианта) и количество потенциальных яхтсменов от 10 до 25. Для уменьшения объема перебора ограничимся вариантами 10, 15, 20, 25 (если полученные выводы для смежных вариантов будут существенно разниться, проведем дополнительный, уточняющий расчет). Итак: X= {Xi} = (2, 3, 4, 5) – количество яхт (i=1,2,3,4); B = {Bj} =(10, 15, 20, 25) – количество членов яхт-клуба (j=1,2,3,4). Для того, чтобы начать поиск решения, построим матрицу решений, элементы которой показывают прибыль при принятии i -го решения при j –ом количестве членов яхт-клуба: aij = 100´min(5´Xi ; Bj) - 170´Xi - 730 т.е. решающее правило в нашей задаче формулируется как "доход – затраты". Например, a11 = 100´min(5´2, 10) - 170´2-730 =-70 a12=100´min(5´2, 15)-170´2-730=-70 a13 = a14 = -70 (спрос на яхты останется неудовлетворенным). Отрицательные значения показывают, что при этих соотношениях спроса на яхты и их наличия яхт-клуб несет убытки. Выполнив расчеты по всем строкам, заполним матрицу решений {aij} ( табл. 6.5): Таблица 6.5. – Ожидаемая прибыль (убыток)
1. Критерий принятия решения Байеса-Лапласа. Предположим, чтоесть статистические данные, позволяющие оценить вероятность того или иного спроса на членство в яхт-клубе: q=(0,1; 0,2; 0,4; 0,3). Тогда математическое ожидание величины прибыли для каждого из рассматриваемых вариантов решения (предложение яхт в яхт-клубе):
Вывод: в условиях рассматриваемой ситуации наиболее целесообразно закупить __________ яхты (в этом случае максимальная ожидаемая прибыль яхт-клуба составит _________ денежных единиц).
2. Для применения критерия Лапласа находим:
Вывод: в условиях равновероятности возникновения той или иной величины спроса на членство в яхт-клубе следует закупить _______ яхты и при этом можно рассчитывать на прибыль в размере ___________ д.е. 3) Критерий Вальда (выбор осторожной, пессимистической стратегии) – для каждой альтернативы (количество яхт в клубе) выбирается самая худшая ситуация (наименьшее значение величины прибыли) и среди них отыскивается гарантированный максимальный эффект: Таблица 6.5– Ожидаемая прибыль (убыток)
ZMM=max(_____; ______; ______; ______)=____ Вывод: принимая решение по критерию Вальда, яхт-клубу следует закупить _________ яхты и максимум ожидаемого убытка не превысит _______ д.е. 4) Критерий Сэвиджа (нахождение минимального риска). При выборе решения по этому критерию сначала матрице полезности сопоставляется матрица сожалений D - для нашего примера, вычитанием (-70) из первого столбца матрицы полезности, 260 из второго столбца, 590 и 920 из третьего и четвертого столбцов соответственно, получим матрицу рисков (см. табл. 6.6): Таблица 6.6 - Матрица рисков
ZS=min(_____;_____;______;_____)=______ Вывод: покупая ______ яхты для открываемого яхт-клуба, мы уверены, что в худшем случае убытки клуба не превысят ________ д.е. 5) Критерий Гурвица (компромиссное решение между самым худшим исходом и излишне оптимистическим). Рассмотреть изменение решения нашей задачи в зависимости от значений коэффициента оптимизма(k=0.2 и k=0.5) Таблица 6.5. - Платёжная матрица
в таблице 6.7 внесем значения, удовлетворяющие критерию Гурвица при различных k): Таблица 6.7 - Решения по Гурвицу для различных k
Вывод: _____________________________________________________ ____________________________________________________________ ____________________________________________________________ ______________________________________________________________ ____________________________________________________________ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 608. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



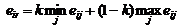
 - это степень доверия к позиции крайней осторожности ZMM. Возьмем
- это степень доверия к позиции крайней осторожности ZMM. Возьмем  , тогда
, тогда 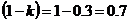 - это степень доверия к позиции критерия азартного игрока
- это степень доверия к позиции критерия азартного игрока
