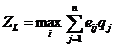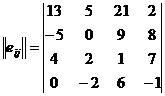ПРИНЯТИЕ И МОНИТОРИНГ ИСПОЛНЕНИЯ РЕШЕНИЙ В РИСК-МЕНЕДЖМЕНТЕ

При принятии решений в условиях неопределенности, когда вероятности возможных вариантов обстановки неизвестны, могут быть использованы критерии, выбор которых, наряду с характером решаемой задачи, поставленных целевых установок и ограничений, зависит также от склонности к риску лиц, принимающих решения. К числу классических критериев, которые используются при принятии решений в условиях неопределенности, можно отнести:

Принцип “недостаточного обоснования” Лапласа

используется если можно предположить, что любой из вариантов обстановки не более вероятен, чем другой. Тогда вероятности обстановки можно считать равными и проводить выбор решения так же, как и в условиях риска, выбирая наилучший средневзвешенный показатель.

Пример.Определить оптимальный вариант(по эффективности) из множества решений, заданных матрицей решений с использованием критерия Лапласа Z_L при равновесных состояниях.

Так как состояния равновесные то, q₁=q₂=q₃=q₄=q₅ q/5=0.2

Каждый элемент матрицы умножаем на вероятность события q, , после этого полученные значения складываются построчно и записываются в дополнительный столбец:

e_i1=1*0.2+3*0.2+2*0.2+5*0.2+0*0.2=2.2

e_i2=

e_i3=

e_i4=

Из дополнительного столбца выбирается максимальное (max) значение. Ответ:

Критерий Байеса-Лапласа

применяется, когда известно распределение вероятностей возможных состояний. Определив математическое ожидание выигрыша для каждого решения, необходимо выбрать то, которое обеспечивает наибольшее значение выигрыша:

Пример.Определить оптимальные варианты (по прибыли) из множества решений, заданных матрицей решений с использованием критерия Байеса-Лапласа Z_BL при следующем распределении вероятностей состояния системы принятия решений: q₁=0,3;q₂=0,3;q₃=0,2;q₄=0,1;q₅=0,1

Вычисления производятся так же, как и в предыдущем примере:

e_i1=

e_i2=

e_i3=

e_i4=

Из дополнительного столбца выбирается максимальное значение (max). Ответ:

Максиминный критерий Вальда

наилучшим решением оказывается то, для которого выигрыш окажется максимальными из всех минимальных при различных вариантах условий.Выбранные таким образом варианты полностью исключают риск, т.к.принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется.

Пример. Определить оптимальные варианты из множества решений, заданных матрицей решений с использованием Критерия Вальда(максиминногоZ_MMкритерия).

Из каждой строки матрицы выбираем минимальный (min) элемент и заносим его в дополнительный столбец, дальше из столбца выбираем максимальный элемент (max).

Ответ: