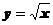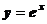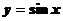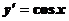Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ГЛАВА 2. Элементы высшей математики.Пределы Пределом функции
Функция, имеющая предел, отличается от него на бесконечно малую величину: Пример. Рассмотрим функцию При стремлении
Основные теоремы о пределах.
1. Предел постоянной величины равен этой постоянной величине
2. Предел суммы (разности) конечного числа функций равен сумме (разности) пределов этих функций.
3. Предел произведения конечного числа функций равен произведению пределов этих функций.
4. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя не равен нулю.
Замечательные пределы
Примеры вычисления пределов Пример 1
Однако, не все пределы вычисляются так просто. Чаще вычисление предела сводится к раскрытию неопределенности типа: Пример 2
Пример 3
Производная функции Пусть мы имеем функцию Аргумент Значению аргумента Значению аргумента Следовательно,
Найдем предел этого отношения при
Определение 3 Производной данной функции
Производная функции 
Определение 4 Операция нахождения производной от функции называется дифференцированием. Механический смысл производной. Рассмотрим прямолинейное движение некоторого твердого тела или материальной точки. Пусть в некоторый момент времени
Через некоторый промежуток времени
Следовательно, определение мгновенной скорости движения материальной точки сводится к нахождению производной от пути по времени.
Геометрическое значение производной Пусть у нас есть графически заданная некоторая функция
Рис. 1. Геометрический смысл производной
Если
Следовательно Таблица основных формул дифференцирования.
Степенная функция
Показательная функция
Логарифмическая функция
Тригонометрическая функция
Обратная тригонометрическая функция
Правила дифференцирования. Производная от Производная суммы (разности) функций Производная произведения двух функций
Производная частного двух функций
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 206. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 является конечное число А, если при стремлении x®x0 для каждого наперед заданного
является конечное число А, если при стремлении x®x0 для каждого наперед заданного  , найдется такое число
, найдется такое число  , что как только
, что как только  , то
, то  .
.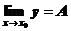
 , где e - б.м.в., т.е.
, где e - б.м.в., т.е.  .
. .
. , функция y стремится к нулю:
, функция y стремится к нулю: 
 .
. .
.

 ,
,  , где
, где 

 или
или  .
. .
.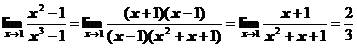 .
. , непрерывную на отрезке
, непрерывную на отрезке  .
.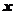 получил некоторое приращение
получил некоторое приращение  . Тогда и функция получит приращение
. Тогда и функция получит приращение 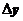 .
. соответствует значение функции
соответствует значение функции 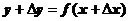 .
. .
.
 . Если этот предел существует, то он называется производной данной функции.
. Если этот предел существует, то он называется производной данной функции.

 ;
; 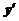 ;
;  ;
;  .
.
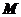 находилась на расстоянии
находилась на расстоянии  от начального положения
от начального положения 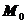 .
.
 она переместилась на расстояние
она переместилась на расстояние  . Отношение
. Отношение 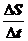 =
=  - средняя скорость материальной точки
- средняя скорость материальной точки  .
.
 .
.
 , будет перемещаться по кривой, приближаясь к точке
, будет перемещаться по кривой, приближаясь к точке 
 , т.е. значение производной при данном значении аргумента
, т.е. значение производной при данном значении аргумента  .
.