
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные элементарные функции.Стр 1 из 12Следующая ⇒ Предисловие Современное естествознание вступило в эру количественных и точных методов познания жизненных процессов. Одним из примеров этого является активное развитие математического моделирования в биологии и медицине с широким привлечением компьютеров и прикладных программ. Очевидно, что без знания основных математических понятий и законов невозможно глубокое изучение физических, физико-химических и физиологических процессов, обеспечивающих жизнедеятельность организма, понимание сущности математического моделирования и др. Трудности, возникающие при решении конкретных количественных биологических и медицинских задач связаны, как правило, с пробелами знаний в различных разделах математики. Настоящее учебное пособие разработано авторами с учетом опыта преподавания курса медицинской и биологической физики. В пособии очень кратко излагаются некоторые темы из курса элементарной математики, знание которых необходимо для понимания дальнейшего теоретического материала высшей математики. Кроме того к каждому разделу даны примеры и задачи и показаны способы их решения. Более подробно рассмотрены колебательные процессы и вопросы математического моделирования в медицине и биологии. ГЛАВА 1. Краткие сведения из элементарной математики. Функция При изучении различных явлений природы и решении целого ряда задач приходится рассматривать изменение одной величины в зависимости от изменения другой. Так, например, пройденный телом путь мы рассматриваем, как величину переменную, изменяющуюся в зависимости от времени, т.е. пройденный путь есть функция времени. 
Определение 1. Если каждому значению переменной Переменная Зависимость переменных
Определение 2. Совокупность значений Способы задания функции I. Табличный способ задания функции При этом способе выписываются в определенном порядке значения аргумента
Таковы, например, таблицы тригонометрических функций. В результате экспериментального изучения физических явлений, как правило, получаются таблицы, выражающие функциональную зависимость между измеряемыми величинами.
II. Графический способ задания функции Если в прямоугольной системе координат на плоскости имеем некоторую совокупность точек Совокупность точек плоскости
III. Аналитический способ задания функции Аналитическим выражением называется символическое обозначение совокупности математических операций, которые необходимо произвести в определенной последовательности над числами и буквами, обозначающими постоянные или переменные величины. Если функциональная зависимость Например:
IV. Параметрический способ задания функции
Даны два уравнения: где каждому значению
Это есть параметрические уравнения окружности. Если мы исключим из этих уравнений параметр
Можно также параметрически задать уравнение эллипса:
Основные элементарные функции. Основными элементарными функциями называются следующие, аналитическим способом заданные функции. I. Степенная функция II. Показательная функция III. Логарифмическая функция IV. Тригонометрические функции V. Обратные тригонометрические функции
Логарифмы и их свойства Логарифмом числа N по основанию а называется показатель степени х, в которую нужно возвести а, чтобы получить число N
Из определения логарифма следует, что Логарифмы по основанию 10 называются десятичными логарифмами. Вместо Логарифмы по основанию e называются натуральными и обозначаются Основные свойства логарифмов. 1) Логарифм единицы при любом основании равен нулю 2) Логарифм произведения равен сумме логарифмов сомножителей. 3) Логарифм частного равен разности логарифмов
4) Логарифм степени равен логарифму модуля основания, умноженному на показатель степени. 5) Логарифм корня равен логарифму модуля подкоренного выражения, деленному на множитель корня. 6) Зависимость между логарифмами с различными основаниями определяется формулой. Множитель С помощью свойств 2-5 часто удается свести логарифм сложного выражения к результату простых арифметических действий над логарифмами. Например, Такие преобразования логарифма называются логарифмированием. Преобразования обратные логарифмированию называются потенцированием.
|
||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 212. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , принадлежащему некоторой области, соответствует одно определенное значение другой переменной
, принадлежащему некоторой области, соответствует одно определенное значение другой переменной  , то
, то  .
. , называется областью определения функции.
, называется областью определения функции. и соответствующие значения функции
и соответствующие значения функции  .
.
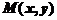 , при этом никакие две точки не лежат на одной прямой, параллельной оси
, при этом никакие две точки не лежат на одной прямой, параллельной оси  , то эта совокупность точек определяет некоторую однозначную функцию
, то эта совокупность точек определяет некоторую однозначную функцию  , абсциссы которых являются значениями независимой переменной, а ординаты - соответствующими значениями функции, называется графиком данной функции.
, абсциссы которых являются значениями независимой переменной, а ординаты - соответствующими значениями функции, называется графиком данной функции. обозначает аналитическое выражение, то значит, что функция
обозначает аналитическое выражение, то значит, что функция  ,
,  ,
,  и т. д.
и т. д. ,
, соответствуют значения
соответствуют значения 
 , то получим уравнение окружности, содержащее только
, то получим уравнение окружности, содержащее только 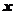 и
и  . Возводя в квадрат параметрические уравнения и складывая, находим:
. Возводя в квадрат параметрические уравнения и складывая, находим: или
или 
 или
или 
 , где
, где  - действительное число.
- действительное число. , где
, где  - положительное число.
- положительное число. , где
, где 

 , при условии, что
, при условии, что 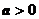 ,
,  ,
, 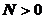
 , т.е.
, т.е.  - это равенство является основным логарифмическим тождеством.
- это равенство является основным логарифмическим тождеством. пишут
пишут  .
. .
.





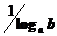 называется модулем перехода от логарифмов при основании a к логарифмам при основании b.
называется модулем перехода от логарифмов при основании a к логарифмам при основании b.