
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Включение пассивного двухполюсника к источнику непрерывно меняющегося напряжения (интеграл Дюамеля).⇐ ПредыдущаяСтр 16 из 16
Реакция цепи на единичную функцию 1(t), называемую функцией Хэвисайда, называется переходной характеристикой цепи
Входной сигнал - может быть напряжением (током). Выходной сигнал – либо ток, либо напряжение на элементах.
Переходные характеристики численно равны току или напряжению на соответствующих элементах. RL – цепь:
RC – цепь: Интеграл Дюамеля можно определить при произведении входных сигналов.
идущих друг за другом непрерывно с одинаковым интервалом Каждый скачок запаздывает на
Элементарные скачки имеют знак «+» для возрастающей Реакция цепи: 1) При 2) При 3) Скачки включаются непрерывно от 4) Интеграл Дюамеля
Примечание: интеграл Дюамеля применим также для входного сигнала, представляющего собой кусочно-аналитическую функцию. Задача:
Глава 8. Операторный и спектральный анализ цепи. Операторный метод расчетов переходных процессов 8.1.1. Метод преобразований по Лапласу. Недостатком классического метода является сложность решения дифференциальных уравнений 2-ого порядка и выше.  Преимущество операторного метода простота записи начальных условий. Они сразу обозначаются на схеме и учитываются при расчете.
Суть метода:
1)
2) Идет расчет цепи в операторной форме: при этом упрощаются операции интегрирования и дифференцирования. Вместо дифференциальных уравнений решаются алгебраические, интегрированные
3) Обратно по времени:
Изображение некоторых функций по Лапласу
1)
2)
3)
Пример:
4) Выражение функций, связанных интегрированием и дифференцированием.
При начальных условиях
Заметим, что в этом методе
Заменяем Аналогичные выражения получатся при интегрировании. Закон Ома в операторной форме.
1) При нулевых начальных условиях:
2) Ненулевые начальные условия:
Если ненулевые начальные условия, то добавляем
2 закон Кирхгофа для этой схемы:
Общий случай закона Ома:
Законы Кирхгофа в операторной форме. 1з.К.: 2з.К.:
При нулевых начальных условиях:
Методы расчета в операторной форме. Законы Кирхгофа в операторной форме похожи по написанию на законы Кирхгофа для цепи постоянного тока, поэтому похожи на все методы расчета. Например, метод узловых потенциалов (МУП):
8.1.5. Переход от изображения к оригиналу.Теорема разложения. Переход совершается следующим способом:
1)
2) по таблицам ;
3) по теореме разложения:
Пример:
Приравниваем
По теореме разложения:
Пример расчета переходных процессов в цепях 2-ого порядка операторным методом.
Дано: Определить
Решение:
1) Определим начальные условия до коммутации
2) Схема после коммутации в операторной форме:
По 2 закону Кирхгофа:
Приравниваем
где
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 417. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |





 ;
;  ;
; 



 ;
;  ;
; 
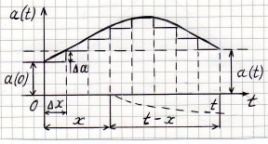 Пусть
Пусть  непрерывно изменяющаяся функция.
непрерывно изменяющаяся функция. запишем входной сигнал из этих сигналов
запишем входной сигнал из этих сигналов  ,
,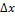 .
. .
. , «-» - для убывающей.
, «-» - для убывающей. действует скачок
действует скачок  и реакция цепи будет
и реакция цепи будет 
 скачок
скачок  .
. до
до  и суммарная реакция цепи:
и суммарная реакция цепи: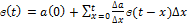



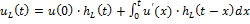




 Определить:
Определить: 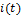

 , где
, где 
 ;
; 



 , где
, где 



 ,
, 





 ,
, 

 , где
, где 





 (1)
(1) (2)
(2)
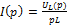
 заменяется на
заменяется на 
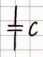

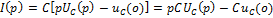 (3)
(3) (4)
(4)
 на
на 










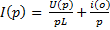









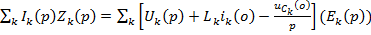



 , где
, где 
 не имеет кратных корней.
не имеет кратных корней. теорема разложения
теорема разложения
 :
:





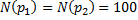



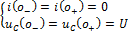










 ,
, 