
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Классический метод анализа переходных процессов.1) Составляется дифференциальные уравнения для конкретной цепи по закону Кирхгофа. 2) Ищется решение этих уравнений при определенных начальных условиях. 7.2.1. Переходные процессы в R , L – цепях. ① Включение R , L – цепи на постоянное напряжение:
Дано: U , R , L Определить:
Решение: 1) Определим начальные условия до коммутации:
2) Схема после коммутации:
неоднородное.
Решение такого уравнения (1) ищется в виде:
1) 2) Решение в виде:
Величина обратная р обозначается:
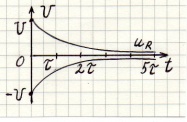
при
Переходный процесс заканчивается за время (3-5
Решение уравнения (1) имеет вид:
А - ? Определяем А из интегрирования начальных условий.
② Короткое замыкание RL – цепи:
Дано: R , U, L Определить: при значении К в положении ②.
Решение: 1) Определяем начальные условия до коммутации: 2) После коммутации:
Определение постоянной интегрирования А из начальных условий: 
Подключение RL – цепи на добавочном сопротивлении.
③ RL – цепь на добавочном сопротивлении. Решение точно такое же. Отличие в том, что:
Если
Мощная электрическая машина выключается через некоторое сопротивление, чтобы исключить пробои изоляции (аварийный режим).
④ RL – цепь на синусоидальном напряжении.
Дано: R , L, Определить: при замыкании К.
Решение:
1) Определение начальных условий до коммутации:
2) После коммутации:
Определим А из начальных условий:
1 случай: Переходной процесс отсутствует.
2 случай: Переходный процесс максимальный.
Пусть
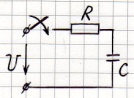
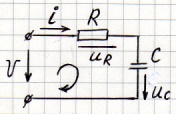
7.2.2. Переходные процессы в RC – цепях. ① Включение RC – цепи на постоянном напряжении.
Дано: R , С, U Определить: после замыкания К
Решение: 1) Определяем начальные условия до коммутации:
2) Схема после коммутации:
3) Решение уравнения (1):
Определяем А из начальных условий:
② Короткое замыкание RC – цепи. (самостоятельно)
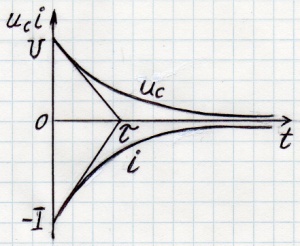
Замыкание накоротко цепи, состоящей из последовательно соединенных R и С, равносильно принятию ЭДС, равной нулю. Предполагается, что емкость C заряжена, т.е. в момент включения на выводах имеется напряжение U. Взяв ЭДС E равной нулю, получим: При коротком замыкании цепи R,C электрический ток идет от вывода (+) к выводу (-). На рисунке показаны кривые спада uc и i:
В отличии от напряжения на емкости, которое изменяется непрерывно, ток в контуре R,C, пропорциональный скорости изменения uc, совершает при t=0 скачок.
Энергия, рассеиваемая в сопротивлении R в течение всего переходного процесса, равна энергии, запасенной в электрическом поле до коммутации:
Так же как и в случае цепи R,L, переходный процесс может считаться законченным спустя t=(4-5)τ, так как к этому времени емкость разрядится на 98,2-99,3% и напряжение на емкости снизится до 1,8-0,7% первоначального.
③ Включение RC – цепи на синусоидальное напряжение:
Дано: R , С, Определить: после замыкания К.
Решение: 1) Начальные условия до коммутации: 2) Схема после коммутации:
Определяем А из начальных условий:
⇒
7.2.3. Переходные процессы в разветвленных цепях: Отличие в том, что составляется не одно уравнение, а несколько по методу законов Кирхгофа
Дано: Определить:
Решение: 1) Начальные условия до коммутации: Метод законов Кирхгофа:
из (3) ⇒
(1) → (2):
Решение уравнения (4):
Определяем А из начальных условий:
| | |
| | |
7.2.4. Переходные процессы 2-ого порядка. 7.2.4.1. Включение R,L,С – цепи на постоянное напряжение.
Дано: R,L,С,U Определить:
Решение: 1) Определяем начальные условия до коммутации: 2) Схема после коммутации:
3) Решение уравнения (1) в виде:
Возможны 3 случая из-за выражения под корнем:
1)
2)
3)
① Апериодический режим:
Определим
1) 2) 3) 4)
Из (2):
где
Из (3):
Из (4):
② Критический режим:
Далее аналогично апериодическому режиму.
③ Колебательный режим:
Определим
Строим график для случая
_____________________________________________________________________________________________ _____________________________________________________________________________________________
При
7.2.4.2. Разряд емкости на RL-цепи .
Так как до коммутации емкость C была заряжена до напряжения U, то имеем ненулевые начальные условия: После коммутации (переключение ключа из положения 1 в положение 2 емкость начнет разряжаться и в цепи возникнет свободный переходный процесс).
1) В первом случае, когда R>2
Для их определения запишем уравнение для тока в цепи:
Постоянные А1 и А2 можно найти из начальных условий для
Из решения системы уравнений следует, что:
В результате получаем уравнения для напряжения uc и тока i:
Закон изменения напряжения на индуктивности определяется при этом уравнением:
Каждая из найденных величин uc, i, uL состоит из двух слагаемых, затухающих по экспоненте с коэффициентами p1<0 и p2<0:
Момент времени t1, соответствующей точке перегиба
Анализ полученных кривых показывает, что в рассматриваемом случае происходит апериодический разряд C, причем в интервале от 0 до t1 энергия Wc расходуется на покрытие тепловых потерь в резистивном сопротивлении R и создание магнитного поля в индуктивности (pc = uci < 0; pL = ULi > 0). В дальнейшем (t > t1) как энергия электрического поля емкости Wc, так и запасенная к моменту t = t1 магнитная энергия индуктивности WL расходуется на покрытие тепловых потерь в сопротивлении R.
2) Во втором случае при R < 2
Закон изменения тока в цепи: Постоянные A и
Отсюда A= Окончательно уравнение для uc, i и uL принимают вид:
Полученные уравнения показывают, что в данном случае имеет место колебательный разряд емкости с частотой wc, зависящей только от параметров R, L, C цепи. Интервал времени Tc =
На рисунке изображены графики зависимостей uc(t) и i(t) определяемых найденными уравнениями. Скорость затухания переодического процесса принято характеризовать декрементом-затухания, который определяют как отношение двух соседних амплитуд тока или напряжения одного знака: На практике чаще используется логарифмический декремент затухания: Из уравнений (1) и (2) следует, что затухание тем больше, чем больше R. При R=2 При R=0 оказываются незатухающие гармонические колебания с частотой Очевидно, что этот случай представляет чисто теоретический интерес, так как в любом реальном контуре имеются потери. В процессе колебательного разряда емкости имеет место попеременное запасание энергии Wc в электрическом поле емкости и магнитном поле индуктивности WL. В начале энергия Wc расходуется на создание магнитного поля WL индуктивности и покрытие тепловых потерь сопротивления R, затем запасенная энергия WL, расходуется на перезаряд емкости и покрытие потерь до полного перехода первоначальной энергии Wc(0) в тепловые потери в резисторе R.
3) Третий случай R = 2
Ток определяется уравнением: A1, A2 – постоянные интегрирования, определяемые из начальных условий для uc и i и законов коммутации:
Отсюда A2 =
По своей форме графики зависимостей (3) аналогичны кривым, изображенным на первом рисунке с той лишь разницей, что их скорость изменения больше, чем при R > 2 Значение R = 2
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 508. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |




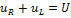
 (1) – линейное дифференциальное уравнение 1-ого порядка,
(1) – линейное дифференциальное уравнение 1-ого порядка,
 - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения. - общее решение однородного уравнения.
- общее решение однородного уравнения.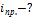




 , где р – корень характеристического уравнения
, где р – корень характеристического уравнения  ⇒
⇒ 
 постоянная времени (цепи)
постоянная времени (цепи)

 это время, за которое свободная составляющая изменяется в е раз.
это время, за которое свободная составляющая изменяется в е раз. ).
).

 при
при 









 принужденный
принужденный свободный
свободный ⇒
⇒ 
 , где
, где 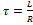
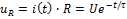
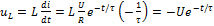




 , то
, то 
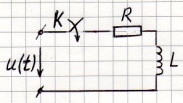





 , где
, где 


 , где
, где 
 , где
, где 
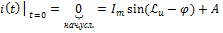 ⇒
⇒ 


 или
или 

 ,
, 

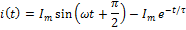






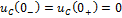





 (1)
(1) 
 где
где  частное решение неоднородного уравнения
частное решение неоднородного уравнения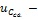 общее решение неоднородного уравнения
общее решение неоднородного уравнения

 , где
, где  корень характеристического уравнения
корень характеристического уравнения 
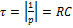 , где
, где  источник времени.
источник времени. , где
, где 


 , где
, где 


 где
где  .
.




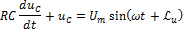
 где
где  цепь с емкостью.
цепь с емкостью. ;
; 

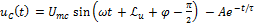 , где
, где  ⇒
⇒








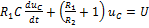 (4)
(4) 
 ;
; 
 ;
; 
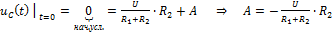


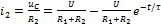


 (в начальный момент) |
(в начальный момент) |  (установившийся)
(установившийся)
 |
|  |
| 
 |
| 
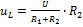 |
| 




 |
|






 (1)
(1)
 ;
; 








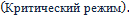


 .
.



 и
и 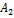 из начальных условий
из начальных условий


 ;
; 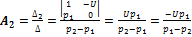
 (2) , где
(2) , где 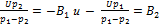
 Нам известно, что:
Нам известно, что: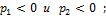







 (3),
(3),



 (4),
(4), где
где 










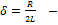 коэффициент затухания.
коэффициент затухания. частота затухания
частота затухания частота собственных колебаний
частота собственных колебаний

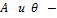 постоянные интегрирования
постоянные интегрирования

 из начальных условий:
из начальных условий:

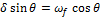








 где
где 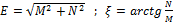

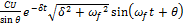 ⊜ , где
⊜ , где 





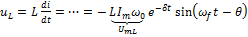

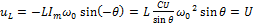 , где
, где 

 декремент амплитуд
декремент амплитуд
 логарифмический
логарифмический .
. корни p1 и p2 будут вещественными и различными:
корни p1 и p2 будут вещественными и различными: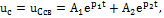 где
где  – постоянные интегрирования.
– постоянные интегрирования.

 и законов коммутации:
и законов коммутации: 




 и нулевому значению uL определяется из решения уравнения
и нулевому значению uL определяется из решения уравнения  а момент t2 из решения уравнения
а момент t2 из решения уравнения 
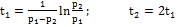

 называют частотой собственных затухающих колебаний.
называют частотой собственных затухающих колебаний. где A и
где A и 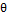 – постоянные интегрирования.
– постоянные интегрирования.




 носит название квазипериода.
носит название квазипериода.
 (1)
(1) (2)
(2)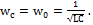

 – корни характеристического уравнения;
– корни характеристического уравнения; .
.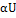 . Окончательные выражения для напряжения и тока принимают вид:
. Окончательные выражения для напряжения и тока принимают вид: (3)
(3)