
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Оценка погрешностей косвенных измеренийПри косвенных измерениях искомая величина А функционально связана с одной или несколькими непосредственно измеряемыми величинами x, y,…,t. Если искомая величина зависти от одной переменной, т. е. A=F(x), то приращение функции будет определяться как A+ΔA = F(x+Δx). Разложив правую часть этого равенства в ряд Тейлора и пренебрегая членами разложения, содержащими Δx в степени выше первой, получим A+ΔA≈F(x)± Относительная ошибка измерения функции определяется выражением
Если измеряемая величина А является функцией нескольких переменных Частные относительные погрешности косвенного измерения определяются по формулам
Относительная погрешность косвенного результата измерений
Пример 2.4. Требуется произвести косвенное измерение мощности. При этом имеются значения тока I и напряжения U, подтверждаемые прямыми измерениями. Пусть U = 220 В, I = 5 А, средние квадратические отклонения напряжения и тока составляют
При сложной нелинейной функции A = F(x, y,…t), отыскание закона распределения погрешности результата связано со значительными математическими трудностями. Поэтому при нелинейных косвенных измерениях приходится отказываться от использования интервальных оценок погрешности результата, ограничиваясь приближенной верхней оценкой ее границ.  Применив формулу (2.8), получим несколько простых правил оценивания погрешности результата косвенного измерения. Для простоты рассмотрим функцию Правило 1. Погрешности в суммах и разностях. Если
Правило 2. Погрешности в произведениях и частных. Если измеренные значения Правило 3. Измеренная величина умножается на точное число. Если Правило 4. Возведение в степень. Если Правило 5. Погрешность в произвольной функции одной переменной. Если
Вывод этих правил не приводится и может быть легко сделан самостоятельно. Использование правил позволяет получить не слишком завышенную оценку предельной погрешности результата нелинейного косвенного измерения при не слишком большом числе аргументов (менее 5). Пример 2.5. Производится косвенное измерение электрической мощности, рассеиваемой на резисторе сопротивлением R = 75±4 Ом при падении напряжения на нем U = 8,6±0,01 В. Так как P=U2/R, то, применяя правила 2 и 4, получим |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 678. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 или ΔA≈±
или ΔA≈± 

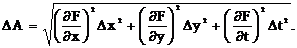 (2.8)
(2.8)


 = 1 В и
= 1 В и 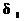 = 0,04 А соответственно. Будем полагать, что доверительная вероятность результата измерения Pд = 0,9944 и tp = 2,77. Расчет мощности будем производить по формуле P = U∙I = 220·5 = 1100 Вт. Тогда абсолютная погрешность измерения будет определяться выражением
= 0,04 А соответственно. Будем полагать, что доверительная вероятность результата измерения Pд = 0,9944 и tp = 2,77. Расчет мощности будем производить по формуле P = U∙I = 220·5 = 1100 Вт. Тогда абсолютная погрешность измерения будет определяться выражением  · tp. Находим значение абсолютной погрешности, полагая ΔU =
· tp. Находим значение абсолютной погрешности, полагая ΔU =  = 28,036. Следовательно, результат измерения мощности можно записать как P = 1100±28 Вт, Pд = 0,9944.
= 28,036. Следовательно, результат измерения мощности можно записать как P = 1100±28 Вт, Pд = 0,9944. ,
,  ).
). и
и  и измеренные значения используются для вычисления суммы или разности
и измеренные значения используются для вычисления суммы или разности  , то суммируются абсолютные погрешности
, то суммируются абсолютные погрешности 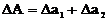 .
. или
или  , то суммируются относительные погрешности
, то суммируются относительные погрешности 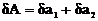 , где
, где  .
. используется для вычисления произведения
используется для вычисления произведения  , в котором В не имеет погрешности, то
, в котором В не имеет погрешности, то  .
. , то
, то  .
.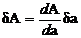 .
.