
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нормирование метрологических характеристик средств измеренийДля обеспечения единства измерений и взаимозаменяемости средств измерений их метрологические характеристики нормируются и регламентируются. Для этого используют нормированные значения погрешности.Под нормированным значением понимается погрешность, являющаяся предельной для данного типа средств измерения. Среди метрологических характеристик можно выделить несколько основных: – градуировочные характеристики, определяющие зависимость выходного – динамические характеристики, отражающие инерционные свойства – инструментальные составляющие погрешности измерения; – функции влияния, отражающие зависимость метрологических характеристик средств измерений от воздействия влияющих величин или неинформативных параметров (напряжение, частота сети, магнитное поле и т. д.).
Метрологические характеристики нормируются для нормальных условий применения средств измерений. Нормальнымисчитаются такие условия, при которых изменением метрологических характеристик под воздействием влияющих величин можно пренебречь. Нормальные условия измерений устанавливаются в нормативных документах на средства измерений конкретного типа. Одной из важнейших метрологических характеристик является погрешность средств измерения – инструментальнаяпогрешность (точность) измерения ими физической величины.  Основная и дополнительная погрешности для средств измерений электрических величин нормируются отдельно. Пределы допускаемых дополнительных погрешностей, как правило, устанавливают в виде дольного значения предела допускаемой основной погрешности. Для оценки дополнительных погрешностей измерений в документации на средство измерения обычно указывают нормы изменения показаний при выходе условий измерения за пределы нормальных. Информация о возможной инструментальной погрешности содержится в указании класса точности средства измерения. В Рекомендациях по межгосударственной стандартизации РМГ 29-99 дается следующее определение класса точности: «Класс точностисредства измерения – обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность». Кроме того, имеется и такое примечание: «Класс точности дает возможность судить о том, в каких пределах находится погрешность средств измерений одного типа, но не является непосредственным показателем точности измерений, выполненных с помощью каждого из этих средств». Последнее связано с тем, что погрешность измерения определяется не только погрешностью средства измерения, но и методом измерений, условиями измерений и т. д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность средства измерения данного типа. Классы точности присваивают средствам измерений при их разработке на основании исследований и испытаний представительной партии устройств данного типа. Класс точности средств измерений конкретного типа устанавливают в стандартах технических требований (условий) или в других нормативных документах. Пределы допускаемых погрешностей нормируют и выражают в форме абсолютной (Δ), относительной (δ) или приведенной (γ) погрешностей. Форма выражения зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и конкретного назначения средства измерения. Пределы допускаемых погрешностей определяются аналогично погрешностям измерений соответственно по формулам (2.1), (2.2) и (2.3). Однако в них вместо результата измерения xдолжно использоваться показание средства измерения (измерительного прибора). В общем случае абсолютная погрешность средств измерений Δ состоит из аддитивной (суммируемой с измеряемой величиной) и мультипликативной (умножаемой на измеряемую величину) составляющих. Причиной возникновения аддитивной составляющей погрешности могут быть: неточность установки на нуль перед измерением, наличие термоЭДС в цепях постоянного тока и т.д. Причинами возникновения мультипликативной погрешности могут быть изменения коэффициента усиления усилителя, коэффициента передачи измерительного преобразователя и т.д. Максимальная основная погрешность измерительного прибора (средства измерения), при которой он разрешен к применению, называется пределом допускаемой основной погрешности. Пределы допускаемой абсолютной основной погрешностиустанавливают по одной из формул или где х – значение измеряемой величины; а, b – положительные числа, не зависящие от х. Первая формула описывает аддитивную погрешность (рис. 2.3а средств измерений. Нормирование в соответствии с выражением (2.5) означает, что в составе погрешности средства измерения присутствует сумма аддитивной и мультипликативной составляющих. Мультипликативная погрешность показана на рис. 2.3б, а сумма аддитивной и мультипликативной составляющих представлена на рис. 2.3в.
а) б) в)
Рис. 2.3
Отметим, что рассмотренные выше выражения и графики погрешностей средства измерения получены для Δ > 0. Однако в практике измерений вполне возможно получение значения Δ < 0. Поэтому в общем случае выражения для абсолютной и относительной погрешностей средства измерения аналитически записываются со знаком « ± ». В формулах (2.4) и (2.5) значения Δ и х выражаются одновременно либо в единицах измеряемой или воспроизводимой мерой величины, либо в делениях шкалы средства измерения. В этих случаях класс точности обозначается заглавными буквами латинского алфавита (например, L, М, С и т. д.), или римскими цифрами (I, II, III и т. д.). К буквам при этом допускается присоединять индексы в виде арабской цифры. Например, класс точности генератора импульсов точной амплитуды Г5-75 обозначается цифрой I [9], а генератор низкочастотный Г3-56/1 относится к классу точности F1U4 [10]. Чем меньше пределы допускаемой погрешности, тем ближе к началу алфавита должна быть буква и тем меньше цифра. Пределы допускаемой приведенной основной погрешностиустанавливают по формуле где р – отвлеченное положительное число, выбираемое из ряда предпочтительных чисел: 1·10n; 1,5·10n; 2·10n; 2,5·10n; 4·10n; 5·10n; 6·10n, (2.6) где n = 1, 0, -1,-2 и т.д.
Нормирующее значение xNвыражается в тех же единицах, что и абсолютная погрешность Δ. Для средств измерений с равномерной, практически равномерной или степенной шкалой значение XNпринимают равным: - большему из пределов измерений или равным большему из модулей пределов измерений, если нулевое значение (нулевая метка) находится на краю или вне диапазона измерений; - сумме модулей пределов измерений, если нулевое значение находится внутри диапазона измерения. Пределы допускаемой относительной основной погрешностиустанавливают следующим образом:
если Δ = ± а. В данном случае q – отвлеченное положительное число, выбираемое из ряда предпочтительных чисел (2.6). При проведении измерений важное значение имеет диапазон измеренийизмерительного прибора. Так как при Δ > 0
то с увеличением x относительная погрешность средства измерения будет уменьшаться (при больших x значением дроби a/x можно пренебречь, т. е. δ≈b). График относительной суммарной погрешности δ показан на рис. 2.4.
Рис. 2.4
Поэтому следует выбирать такой диапазон измерений, в котором значение х близко к Хк – большему (по модулю) из пределов измерений. Когда допускаемая абсолютная основная погрешность задана формулой (2.5), пределы допускаемой относительной основной погрешности устанавливают согласно выражению где с – суммарная относительная погрешность прибора; d – аддитивная относительная погрешность прибора; Хк – конечное значение диапазона измерений; с, d – отвлеченные положительные числа, выбираемые из ряда предпочтительных чисел (2.6). Числа а ,b, c, d в (2.5) и (2.7) связаны между собой следующим образом: c = b + d; d = a/|XK|, причем c>d. Классы точности приборов, пределы допускаемой относительной основной погрешности которых принято выражать в виде дольного значения предела допускаемой основной погрешности, т.е. по формуле (2.7), обозначают числами с и d (в процентах), разделяя их косой чертой (например, класс точности цифрового вольтметра Ф292 для предела измерения 10 В обозначается как 0,2/0,1 [11]). Предел допускаемой абсолютной дополнительной погрешности средства измерения Δдси может указываться в виде: – постоянного значения для всей рабочей области влияющей величины – отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины, к этому – зависимости предела Δдси от влияющей величины.
В некоторых случаях дополнительная погрешность прибора указывается в виде дольного значения основной относительной погрешности. Так, например, для цифрового вольтметра Ф292 допускаемая дополнительная погрешность, вызванная воздействием внешнего однородного магнитного поля с индукцией
Пример 2.2. Отсчетное устройство вольтметра среднего квадратического значения с классом точности 0,5 (приведенная погрешность) имеет пределы 0 и 200 В. Указатель показывает напряжение 110 В. Необходимо определить, чему равно измеряемое напряжение. Решение. Для данного прибора предел допускаемой приведенной основной погрешности определяется как γ = (Δ/Xк)·100 %. При этом γ не превышает 0,5. Отсюда находим значение Δ ≤ ± 1В. Следовательно, измеряемое напряжение: Пример 2.3. Класс точности используемого при измерениях вольтметра указан как c/d = 0,06/0,04. Показываемое значение напряжения x=25В Предел измерения Xк = 100В. Определить абсолютную погрешность измерения. Решение. Прежде всего, требуется вычислить относительную погрешность результата измерения:
Вычислив значение δ, мы можем перейти к абсолютной погрешности измерения, выразив ее из формулы
Находим абсолютную погрешность результата измерения (в данном случае предполагается, что погрешность измерения полностью определяется инструментальной погрешностью): Δ = ±δ·x/100 = ±0,18·25/100≈±0,05 В.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 560. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (2.4)
, (2.4) , (2.5)
, (2.5)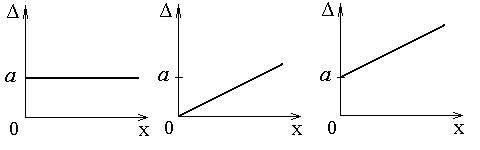
 ,
,  ,
, ,
,
 , (2.7)
, (2.7) .
. .
.