
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обработка прямых измерений с многократными наблюдениямиРассмотрим группу из N независимых результатов наблюдений случайной величины x и определим последовательность ее обработки. Правила обработки результатов измерения с многократными наблюдениями учитывают следующие факторы: – обрабатывается ограниченная группа из n наблюдений; – результаты наблюдений – в группе наблюдений могут встречаться грубые погрешности; – распределение случайных погрешностей может отличаться от нормального.
Обработка результатов наблюдений производится в следующей последовательности [12]: 1. Исключить известные систематические погрешности из результатов наблюдений (введением поправки). 2. Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения:
3. Вычислить оценку среднего квадратического отклонения результатов наблюдения
Вычислив оценку СКО результата наблюдений, целесообразно проверить наличие в группе наблюдений грубых погрешностей (при нормальном законе распределения ни одна случайная погрешность, с вероятностью практически равной единице, не может выйти за пределы 4.Вычислить оценку СКО результата измерения по формуле
5. Проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению. При числе наблюдений n<15 принадлежность их к нормальному распределению не проверяют, а доверительные границы случайной погрешности результата определяют лишь в том случае, если достоверно известно, что результаты наблюдений принадлежат нормальному закону.  6. Вычислить доверительные границы Δг случайной погрешности результата измерения при заданной вероятности Рд: Δг = где tp – коэффициент Стьюдента. 7. Вычислить границы суммарной неисключенной систематической Неисключенная систематическая погрешность результата образуется из неисключенных систематических погрешностей метода, средств измерений, погрешностей поправок и др. При суммировании эти составляющие рассматриваются как случайные величины. При отсутствии данных о виде распределения неисключенных составляющих систематических погрешностей их распределения принимают за равномерные. При равномерном распределении неисключенных систематических погрешностей границы неисключенной систематической погрешности результата измерения
где Доверительную вероятность для вычисления границ НСП принимают той же, что при вычислении границ случайной погрешности результата измерения. 8. Вычислить доверительные границы погрешности результата измерения. Анализ соотношения между неисключенной систематической погрешностью и случайной погрешностью показывает, что если Если оба неравенства не выполняются, вычисляют СКО результата как сумму неисключенной систематической погрешности и случайной составляющей:
Границы погрешности результата измерения в этом случае вычисляют по формуле
При симметричном доверительном интервале погрешности результат измерения представляют в форме При отсутствии данных о видах функции распределения составляющих погрешности результата или при необходимости дальнейшей обработки результатов результат измерения представляют в форме
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 527. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 могут содержать систематическую погрешность;
могут содержать систематическую погрешность; .
. .
. ). Наблюдения, содержащие грубые погрешности, исключают из группы и заново повторяют вычисления
). Наблюдения, содержащие грубые погрешности, исключают из группы и заново повторяют вычисления и
и  .
. .
. ,
,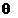 вычисляют по формуле
вычисляют по формуле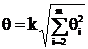 ,
, – граница i-й неисключенной составляющей систематической погрешности; k – коэффициент, определяемый принятой доверительной вероятностью (при Рд=0,95 k=1,1); m – количество неисключенных составляющих.
– граница i-й неисключенной составляющей систематической погрешности; k – коэффициент, определяемый принятой доверительной вероятностью (при Рд=0,95 k=1,1); m – количество неисключенных составляющих. , то неисключенной систематической погрешностью можно пренебречь и принять границы погрешности результата равными Δг. Если
, то неисключенной систематической погрешностью можно пренебречь и принять границы погрешности результата равными Δг. Если 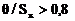 , то случайной погрешностью можно пренебречь и принять границы погрешности результата равными
, то случайной погрешностью можно пренебречь и принять границы погрешности результата равными  .
. .
. . Коэффициент К в данном случае вычисляют по эмпирической формуле
. Коэффициент К в данном случае вычисляют по эмпирической формуле .
. , Рд.
, Рд. , N,
, N,