
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Параболический тренд и его свойстваПод названием параболического будем иметь в виду тренд, выраженный параболой 2-го порядка с уравнением: Значения (смысл, сущность) параметров параболы 2-го порядка таковы: свободный член
Следовательно, тренд в форме параболы 2-го порядка применяется для отображения таких тенденций динамики, которым свойственно примерно постоянное ускорение абсолютных изменений уровней (рост населения отдельных городов или регионов, ускоренное увеличение объема продукции в фазе циклического подъема, динамика экспорта). Основные свойства тренда в форме параболы 2-го порядка таковы: 1. Неравные, но равномерно возрастающие или равномерно убывающие абсолютные изменения за равные промежутки времени. 2. Парабола, рассматриваемая с точки зрения ее математической формы, имеет две ветви: восходящую с увеличением уровней признака, и нисходящую с их уменьшением. Но с точки зрения статистики, по содержанию изучаемого процесса изменений, трендом, выражающим определенную тенденцию развития, чаще всего можно считать только одну из ветвей: либо восходящую, либо нисходящую. В особых, более редких конкретных ситуациях мы не отрицаем возможности объединения обеих ветвей в единый тренд.  3. Так как свободный член уравнения а) При б) При в) При г) При 4. При параболической форме тренда, в зависимости от соотношений между его параметрами, цепные темпы изменений могут либо уменьшаться, либо некоторое время возрастать, но при достаточно длительном периоде времени рано или поздно темпы роста всегда обязательно начинают уменьшаться, а темпы сокращения уровней при |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 543. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

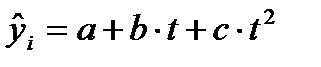 . Парабола 3-го и более высоких порядков редко применимы для выражения тенденции динамики и слишком сложны для получения надежных оценок параметров при ограниченной длине временного ряда. Прямую линию, с точки зрения математики, можно также считать видом парабол – параболой 1-го порядка, которая уже рассмотрена ранее.
. Парабола 3-го и более высоких порядков редко применимы для выражения тенденции динамики и слишком сложны для получения надежных оценок параметров при ограниченной длине временного ряда. Прямую линию, с точки зрения математики, можно также считать видом парабол – параболой 1-го порядка, которая уже рассмотрена ранее.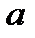 – это средний (выравненный) уровень тренда на момент или период, принятый за начало отсчета времени, т.е.
– это средний (выравненный) уровень тренда на момент или период, принятый за начало отсчета времени, т.е. 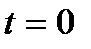 .
.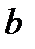 – это средний за весь период среднегодовой прирост, который уже не является константой, а изменяется равномерно со средним ускорением, равным 2
– это средний за весь период среднегодовой прирост, который уже не является константой, а изменяется равномерно со средним ускорением, равным 2  , которое и служит константой, главным параметром параболы 2-го порядка.
, которое и служит константой, главным параметром параболы 2-го порядка.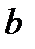 >
> 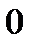 и
и 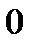 имеем восходящую ветвь, то есть тенденцию к ускоренному росту уровней;
имеем восходящую ветвь, то есть тенденцию к ускоренному росту уровней;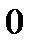 и
и