
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Выборочные оценки числовых индексов воспроизводимости
1.В литературе и нормативных документах, посвященных статистическому контролю производственных процессов, в недавнее время широкое распространение получила методика оценки значимости технологического рассеяния и правильности настройки посредством так называемых индексов воспроизводимости:
где D- полуширина поля допуска; s- СКО технологического рассеяния; m - фактический номинал настройки процесса; а и b- соответственно нижняя и верхняя границы поля допуска. Вероятностный и «физический» смысл величин Пусть 2. При выводе ПР выборочного 
Таким образом, поскольку Закон распределения выборочного Плотность совместного распределения СВ
0
Рис. 5.3.1. Схема области интегрирования для определения
Дифференцируя (5.3.4) по
Рис. 5.3.2. Схема области интегрирования для определения В этом случае
После дифференцирования по
3. Как видно из формул (5.3.5), (5.3.7),
Главным доводом в пользу этого является существенное повышение эффективности оценок (СКО «штрихованных» статистик примерно в 4 раза меньше, чем у исходных). Кроме того, устанавливается единообразие с другими числовыми показателями качества: с оценкой вероятности выхода несоответствующей единицы продукции, оценкой доли несоответствующих единиц продукции в партии, рисков поставщика и потребителя и т.д., где идеальному процессу соответствуют нулевые значения показателей. В предлагаемом варианте область значений удовлетворительного процесса составит
Рис. 5.3.3. Плотности распределения величин
Список Литературы 1. Бернштейн, С.Н. Теория вероятностей. / C.Н. Бернштейн.— Изд. 4-е перераб. И доп. М.-Л.: ОГИЗ, 1946. 2. Вентцель, Е.С., Овчаров, Л.А. Теория вероятностей и ее инженерные приложения / Е.С. Вентцель, Л.А. Овчаров.— М.: Высш. шк., 2000. 3. Вентцель, Е.С., Овчаров, Л.А Теория случайных процессов и ее инженерные приложения / Е.С. Вентцель, Л.А. Овчаров.— М.: Высш. шк., 2003. 4. Крамер, Г. Математические методы статистики / Г. Крамер.— М.: Мир, 1976. 5. Корн, Г., Корн, Т. Справочник по математике / Г. Корн, Т. Корн.— М.: Наука, 1984. 6. Макаров, В.В. Mathcad – 2001 учебный курс / В.В. Макаров. — С.Пб.: Питер, 2004. 7. . Смирнов, Н.В., Барковский, И.В. Теория вероятностей и математическая статистика в технике (общая часть) / Н.В. Смирнов, И.В. Барковский.— М.; Наука, 1965. 8. Плотников, А.Н. Закон распределения длины максимальной серии и его статистические приложения / А.Н. Плотников // Известия СНЦ РАН, 2006. Т. 8, №4- С.1047-1056. 9. Плотников, А.Н. Об инвариантах структуры серий и критериях случайности последовательной выборки./ А.Н. Плотников // Известия СНЦ РАН, 2006. Т.8, №4.- С.1142-1147. 10. Феллер, В. Введение в теорию вероятностей и ее приложения Т.1 / В. Феллер.— М.: Мир, 1983. 11. Финни, Д. Введение в теорию планирования эксперимента / Д. Финни.— М.: Наука, 1970. 12. Хикс, Ч. Основные принципы планирования эксперимента / Ч. Хикс.— М.: Мир, 1997. Приложение I
|
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 357. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и 
 при таком определении вполне прозрачен и не вызывает никакой двусмысленности. Однако на практике числовые характеристики m и s, как правило, неизвестны и заменяются выборочными оценками
при таком определении вполне прозрачен и не вызывает никакой двусмысленности. Однако на практике числовые характеристики m и s, как правило, неизвестны и заменяются выборочными оценками  (п.1.4). При этом объем выборки обычно невелик и составляет порядка 50 значений. В данной ситуации
(п.1.4). При этом объем выборки обычно невелик и составляет порядка 50 значений. В данной ситуации  . (5.3.1)
. (5.3.1) - «точное» значение индекса
- «точное» значение индекса  (принято руководствоваться двумя контрольными нормативами:
(принято руководствоваться двумя контрольными нормативами:  - удовлетворительная воспроизводимость,
- удовлетворительная воспроизводимость, 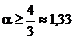 – хорошая воспроизводимость). Выборочную оценку
– хорошая воспроизводимость). Выборочную оценку  преобразуем к виду
преобразуем к виду  . Таким образом, при любом значении s (от m Ср, в принципе, не зависит) ПР выборочной
. Таким образом, при любом значении s (от m Ср, в принципе, не зависит) ПР выборочной  идентична ПР СВ
идентична ПР СВ 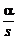 , где s - выборочное СКО стандартной нормальной совокупности. Искомую ПР величины
, где s - выборочное СКО стандартной нормальной совокупности. Искомую ПР величины  (п.1.1):
(п.1.1): . (5.3.2)
. (5.3.2) будем полагать, что процесс настроен на центр поля допуска (
будем полагать, что процесс настроен на центр поля допуска (  ). В этом случае точные значения
). В этом случае точные значения 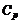 и
и  . Из определения
. Из определения  очевидно, что его можно представить в виде
очевидно, что его можно представить в виде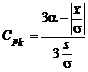 . (5.3.3)
. (5.3.3) не зависит от
не зависит от 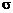 , достаточно рассмотреть выборку из
, достаточно рассмотреть выборку из  . При этом ограничение
. При этом ограничение  также несущественно и при
также несущественно и при  сводится лишь к сдвигу по параметру
сводится лишь к сдвигу по параметру  .
.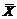 и
и 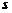 . Сначала, согласно общей методике (п.1.3), найдем
. Сначала, согласно общей методике (п.1.3), найдем  . Для этого придется рассмотреть 2 случая:
. Для этого придется рассмотреть 2 случая:  и
и  (рис.5.3.1, 5.3.2).
(рис.5.3.1, 5.3.2). (5.3.4)
(5.3.4)






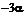


 в координатах
в координатах  при
при 
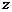 , находим:
, находим: (5.3.5)
(5.3.5)
 в координатах
в координатах  при
при 
 будет иметь вид
будет иметь вид . (5.3.6)
. (5.3.6) (5.3.7)
(5.3.7) имеет, вообще говоря, особенность в точке
имеет, вообще говоря, особенность в точке 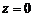 . Однако эта особенность является устранимой (непрерывность в точке
. Однако эта особенность является устранимой (непрерывность в точке  и
и  , определить величину смещения и скомпенсировать его по аналогии с выборочными дисперсией и СКО (п.1.4) посредством поправочных коэффициентов. Однако даже с учетом этих уточнений придется признать, что общепринятая на сегодняшний день методика определения числовых индексов воспроизводимости сформулирована не совсем удачно. Более рациональным представляется перейти к обратным величинам:
, определить величину смещения и скомпенсировать его по аналогии с выборочными дисперсией и СКО (п.1.4) посредством поправочных коэффициентов. Однако даже с учетом этих уточнений придется признать, что общепринятая на сегодняшний день методика определения числовых индексов воспроизводимости сформулирована не совсем удачно. Более рациональным представляется перейти к обратным величинам: .
. , хорошего –
, хорошего –  вместо
вместо  . Их ПР легко вычисляются с помощью преобразования
. Их ПР легко вычисляются с помощью преобразования  (п.1.1), и возникающее отрицательное смещение можно без проблем компенсировать. Однако более предпочтительным с точки зрения практической применимости представляется определение для каждого нормативного значения одностороннего доверительного (90%-95%) интервала, выход за верхнюю границу которого естественно интерпретировать как разладку процесса. Сравнительный вид ПР величин
(п.1.1), и возникающее отрицательное смещение можно без проблем компенсировать. Однако более предпочтительным с точки зрения практической применимости представляется определение для каждого нормативного значения одностороннего доверительного (90%-95%) интервала, выход за верхнюю границу которого естественно интерпретировать как разладку процесса. Сравнительный вид ПР величин 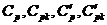 приведен на рис.5.3.3.
приведен на рис.5.3.3.
 при
при 