
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Анализ схем статистического регулирования1.Под статистическим регулированием (не всегда осознанно) подразумевается некий алгоритм автоматического регулирования или, в более общей постановке, наличие системы автоматического управления процессом. Ключевым элементом такой системы, как явствует из выводов соответствующей теории автоматического управления (ТАУ), является отрицательная обратная связь, формирующая релаксирующий управляющий сигнал на выход процесса. В связи с этим следует уточнить смысловое содержание самого термина статистическое регулирование (управление). В контексте положений ТАУ статистическое управление является не каким-то специальным «прогрессивным» способом автоматического управления, а всего лишь его суррагатом, или управлением со значимым запаздыванием, поскольку управляющий сигнал формируется апостериорно, после реализации выходного сигнала. По образному выражению одного из последователей В. Шухарта и Э. Дэминга, статистическое управление похоже «…на управление автомобилем через зеркало заднего вида…». К этому можно было бы добавить, что зеркало является не идеально чистым и отражает лишь усеченную информацию о выходе процесса. В п.5.1 были рассмотрены модели процессов, формируемых трендами среднего  Еще одним допущением, необходимым для применимости статистического моделирования методом Монте‑Карло, является переход к дискретному времени, т. е. будем полагать, что в каждую фиксированную единицу времени формируется 1 отсчет регулируемого процесса (входного сигнала по отношению к системе регулирования) и 1 отсчет управляющего сигнала. 2. Для лучшего уяснения сути дела рассмотрим простейшую схему. Пусть выход процесса есть композиция входного и управляющего сигналов:
Управляющий сигнал
где 0<h<1 – коэффициент передачи обратной связи. Тогда выходной сигнал будет иметь следующий вид:
Пусть в сигнале Таким образом, частичная компенсация разладки
Оптимальным значением h=h* естественно принять точку минимума зависимости (5.2.5), вид которой показан на рис. 5.2.1.
Рис.5.2.1. Оценка вероятности брака в зависимости от
Рассмотренная простейшая схема является, вообще говоря, не совсем статистической, поскольку управляющий сигнал формируется по одному отсчету выходного. Однако и из нее можно извлечь поучительный вывод, заключающийся в том, что при h=1 система очень быстро идет «в разнос» по рассеянию (sy неограниченно возрастает). Согласно принятой в ТАУ терминологии, такая ситуация квалифицируется как потеря устойчивости. Соответственно схема регулирования, когда управляющим сигналом служит отклонение индивидуального значения выхода от номинала, является совершенно непригодной. 3. При формировании управляющего сигнала по скользящему среднему
Диаграммы процесса с разладкой по смещению а б Рис.5.2.2. Диаграмма (временная развертка) (а) и гистограмма (б) процесса с внезапной разладкой по среднему, регулируемого по схеме (5.2.6), в сравнении с исходным (нерегулируемым)
Для исследования асимптотики схемы (5.2.6) положим, что n велико
Применяя операцию МО к обеим частям (5.2.7) и полагая, что существует
откуда находим Аналогично для где Умножая обе части (5.2.7) на Yn-1 и применяя к обеим частям полученного тождества операцию МО, получим На основании результатов п.1.2 соотношения (5.2.9) и (5.2.11), с учетом независимости пары (Xn, Yn-1), преобразуем к рекурсивному соотношению:
откуда находим
Правая часть (5.2.12) тождественно равна нулю, следовательно, Подставляем (5.2.13) в (5.2.10), окончательно получаем
Как видно из последнего соотношения, область устойчивости схемы статистического регулирования по скользящему среднему порядка m=2 составляет 0£h£2. При этом предельно достижимая компенсация отклонения среднего составляет Одним из принципиальных вопросов всякого автоматического управления, и в особенности статистического, является поведение процесса при излишней регулировке. В данном контексте ответ на него вполне очевиден. При использовании схемы (5.2.7) в условиях фактического отсутствия разладки (mХ=0) будет происходить такая же потеря точности мгновенного рассеяния Для оптимизации схемы (5.2.7) по параметру h можно сформулировать задачу, аналогичную (5.2.5). 4. Рассмотрим схему регулирования по скользящим средним с m=3:
Для
Для
откуда следует
где
Последовательно умножая (5.2.15) на Решив систему уравнений (5.2.18), находим Подставив (5.2.19) в (5.2.17), окончательно получаем Таким образом, область устойчивости схемы с m=3 составляет 0£h<3 при предельно достижимой компенсации 5. Для произвольного m можно показать, что
Примеры модельных реализаций процессов с различными вариантами разладок, компенсируемых по схеме скользящего среднего с
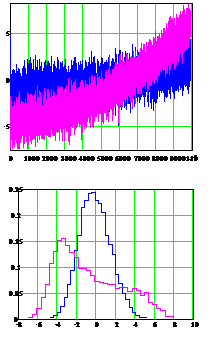
Рис.5.2.5. Диаграмма и гистограмма процесса с осциллирующим трендом среднего, регулируемого по схеме скользящего среднего с
Как видно из графиков, диаграмма ( временная развертка процесса), отражающая последовательность индивидуальных значений, является более информативной, нежели гистограмма. Точки на диаграмме могут отображать индивидуальные значения не подряд, а с некоторой периодичностью, либо отображать статистики (среднее, медиана, СКО, размах) последовательных малых выборок. Такая форма представления исходных данных применительно к контролю технологических процессов была предложена В. Шухартом и Э. Демингом, а затем, стараниями их горячих последователей, была канонизирована и получила название «метод контрольных карт». Методика работы с контрольными картами весьма широко представлена как в литературе, так и в нормативных документах (стандарты, Т/У и т.д.), что избавляет от необходимости подробно на них останавливаться. Хотя, к слову сказать, в некоторых публикациях можно встретить глубокомысленные рассуждения о контурах грядущей всеобъемлющей «теории контрольных карт». В ответ на это можно лишь заметить, что под теорией обыкновенно понимается информационный эквивалент некоего реально существующего (самостоятельного) феномена. Контрольные карты таковыми конечно же не являются. Контрольные карты, при всем их кажущемся многообразии, в основе своей имеют общие довольно простые априорные положе-ния: – контролируемый параметр является СВ с типовым законом распределения; – нормальным, если СВ является непрерывной; – биномиальным или пуассоновским, если СВ целочисленная; – контрольные границы для всех карт определяются «стандартным 6s» интервалом (о законах распределения выборочных статистик см. п.1.5). Финансисты и метеорологи, по-видимому, будучи людьми бо-лее прагматичными, попросту отображают графически индивидуальные значения последовательной выборки, пытаясь экстраполировать тренды и предугадать скачки. При этом скромно именуют свои графики диаграммами.
|
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 362. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
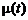 и СКО
и СКО 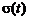 мгновенного нормального распределения. Соответственно, идеально настроенный процесс характеризуется постоянными значениями параметров нормального закона
мгновенного нормального распределения. Соответственно, идеально настроенный процесс характеризуется постоянными значениями параметров нормального закона 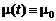 ,
, 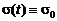 , и без ограничения общности достаточно рассмотреть стандартную нормальную совокупность N(0,1). Разладки условимся классифицировать по характеру зависимостей
, и без ограничения общности достаточно рассмотреть стандартную нормальную совокупность N(0,1). Разладки условимся классифицировать по характеру зависимостей 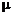 и
и 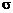 меняются скачком от идеальных значений
меняются скачком от идеальных значений 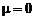 ,
, 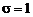 , и параметрические (постепенные), когда
, и параметрические (постепенные), когда 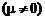 и разладку по рассеиванию
и разладку по рассеиванию 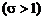 . Последний классифицирующий признак обусловлен следующими соображениями. Устранение разладки по рассеиванию в «физической» интерпретации требует ремонта изношенного оборудования либо его замены на образцы с более высокой точностью, т. е. связано с остановкой процесса. Разладка по смещению центра настройки может быть устранена в автоматическом режиме, без остановки процесса, и потому в дальнейшем изложении ограничимся рассмотрением только разладок по смещению центра настройки.
. Последний классифицирующий признак обусловлен следующими соображениями. Устранение разладки по рассеиванию в «физической» интерпретации требует ремонта изношенного оборудования либо его замены на образцы с более высокой точностью, т. е. связано с остановкой процесса. Разладка по смещению центра настройки может быть устранена в автоматическом режиме, без остановки процесса, и потому в дальнейшем изложении ограничимся рассмотрением только разладок по смещению центра настройки.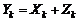 . (5.2.1)
. (5.2.1)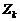 определим в виде отрицательной обратной связи с запаздыванием:
определим в виде отрицательной обратной связи с запаздыванием: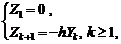 (5.2.2)
(5.2.2)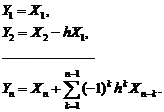 (5.2.3)
(5.2.3)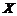 возникла внезапная разладка
возникла внезапная разладка 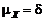 (при неизменном СКО
(при неизменном СКО 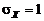 ). Тогда, с учетом априорной независимости в совокупности последовательности
). Тогда, с учетом априорной независимости в совокупности последовательности 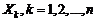 , устремив
, устремив 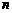 →
→ 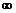 и суммируя образующиеся геометрические прогрессии, находим:
и суммируя образующиеся геометрические прогрессии, находим: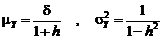 . (5.2.4)
. (5.2.4)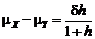 достигается за счет увеличения дисперсии
достигается за счет увеличения дисперсии 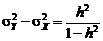 , и возникает задача оптимизации схемы по параметру h по критерию минимальной оценки вероятности результирующего брака. В качестве такой оценки можно принять вероятность выхода за границы «стандартного
, и возникает задача оптимизации схемы по параметру h по критерию минимальной оценки вероятности результирующего брака. В качестве такой оценки можно принять вероятность выхода за границы «стандартного 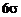 » интервала. Обозначив относительное смещение центра
» интервала. Обозначив относительное смещение центра 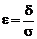 , оценку после элементарных преобразований получим в виде
, оценку после элементарных преобразований получим в виде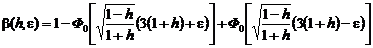 . (5.2.5)
. (5.2.5)
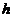 при значениях смещения
при значениях смещения 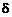 в долях
в долях 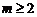 отсчетов выходного возникает уже собственно статистическое регулирование, и при любом
отсчетов выходного возникает уже собственно статистическое регулирование, и при любом 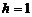 находится в области устойчивости. При
находится в области устойчивости. При 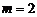 схема будет иметь вид
схема будет иметь вид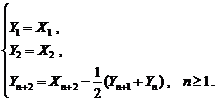 (5.2.6)
(5.2.6)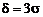 в сравнении с регулируемым по схеме (5.2.6) показаны на рис. 5.2.2.
в сравнении с регулируемым по схеме (5.2.6) показаны на рис. 5.2.2.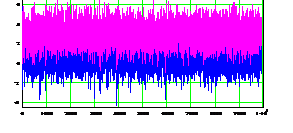
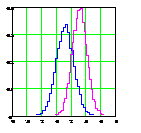
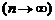 , и рассмотрим ретроспективное рекуррентное соотношение (5.2.6), при произвольном h:
, и рассмотрим ретроспективное рекуррентное соотношение (5.2.6), при произвольном h: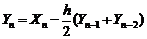 . (5.2.7)
. (5.2.7)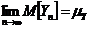 , приходим к рекурсивному соотношению:
, приходим к рекурсивному соотношению: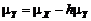 , (5.2.8)
, (5.2.8)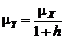 . (5.2.9)
. (5.2.9)
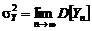 , с учетом независимости пары
, с учетом независимости пары 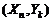 при любом
при любом 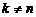 , получим
, получим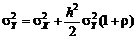 , (5.2.10)
, (5.2.10)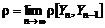 - предельное значение коэффициента корреляции между соседними выходными отсчетами.
- предельное значение коэффициента корреляции между соседними выходными отсчетами.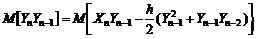 . (5.2.11)
. (5.2.11) ,
,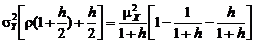 . (5.2.12)
. (5.2.12)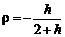 . (5.2.13)
. (5.2.13)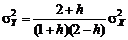 . (5.2.14)
. (5.2.14)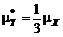 .
.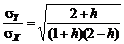 , но уже без полезного эффекта
, но уже без полезного эффекта 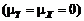 .
.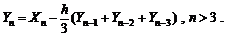 (5.2.15)
(5.2.15)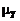 получим соотношение, аналогичное (5.2.9):
получим соотношение, аналогичное (5.2.9):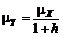 . (5.2.16)
. (5.2.16)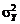 , действуя аналогично случаю
, действуя аналогично случаю 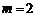 , получим
, получим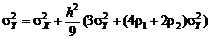 ,
,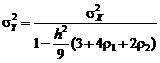 , (5.2.17)
, (5.2.17)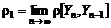 ,
, 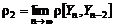 .
.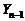 ,
, 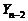 и действуя аналогично случаю m=2, получим систему двух уравнений для определения
и действуя аналогично случаю m=2, получим систему двух уравнений для определения 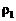 и
и 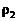 :
: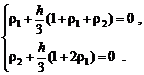 (5.2.18)
(5.2.18)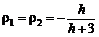 . (5.2.19)
. (5.2.19)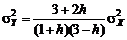 . (5.2.20)
. (5.2.20)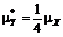 .
.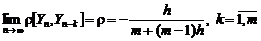 , (5.2.21)
, (5.2.21)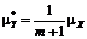 , (5.2.22)
, (5.2.22) . (5.2.23)
. (5.2.23)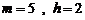 , приведены на рис.5.2.3-5.2.5.
, приведены на рис.5.2.3-5.2.5.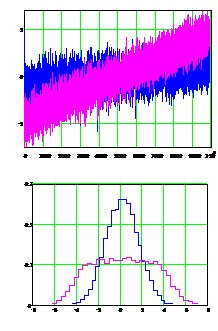

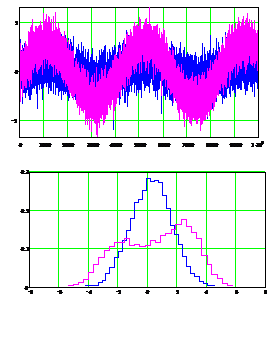
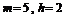 , в сравнении с исходным
, в сравнении с исходным