
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Парадокс инспекции и смежные вопросы1. Сами по себе числовые характеристики (4.1.8) носят сугубо иллюстративный характер, и собственно задача про счастливый билет выбрана из большого ряда аналогичных комбинаторно-вероятностных схем для большей занимательности и наглядности. Гораздо более принципиально важным является фундаментальное свойство геометрического распределения, для иллюстрации которого и был приведен этот демонстрационный пример. Зададимся вопросом: какова будет сравнительная продолжительность ожидания покупки счастливого билета, если в одном случае вести отсчет от очередного счастливого билета, а в другом – от первого попавшегося? Предположим, что из первых k испытаний ни одно не привело к успеху, тогда условная вероятность успеха в (k+1) -ом составит
Подставляя в (4.2.1) ряд распределения, получим
Таким образом, знание «истории» никак не влияет на прогноз относительно результата очередного испытания. Стало быть, каждый билет может считаться первым, и на поставленный вопрос можно дать вполне определенный ответ: время ожидания не зависит от начала отсчета, и «счастливчик» имеет ровно такие же шансы на очередной успех, как и его менее удачливый попутчик. 2. Из независимости от начала отсчета следует, что в качестве него может служить произвольная (случайная) точка t* на оси t. Но тогда расстояние до ближайшего следующего события потока (вре-мя ожидания R) и время, прошедшее от ближайшего предыдущего события (время опоздания Q на рис.4.2.1), имеют такой же закон распределения, как и интервал между событиями. В силу стационарности потока R и Q независимы, стало быть, их сумма – интервал, накрывающий случайную точку t* имеет распределение Эрланга второго порядка: 
Рис. 4.2.1. Схема расположения событий потока на оси времени
Но, с другой стороны, интервал между соседними событиями имеет показательную ПР
а Легко заметить, что оба выражения (4.2.4) можно объединить в одно:
Ряд (4.2.5) сдвигается в сторону большего значения tk, и среднее
Для численной иллюстрации положим Таблица 4.2.1
Увеличивая количество возможных значений интервала и переходя в пределе к непрерывной ПР fT(t), получим следующее соотношение где В частности, для показательной ПР 3. Рассмотренная интерпретация является проявлением закономерности более общего характера. Пусть вероятность попадания случайной точки в область пространства, соответствующую dx пропорциональна
где Пусть, например, fX(x) — ПР гранулометрического спектра порошкового материала (удельная доля числа частиц диаметром
Разрешая (4.2.8) относительно fX с учетом (4.2.10), получим: |
|||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 439. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
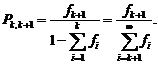 (4.2.1)
(4.2.1)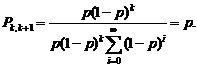 (4.2.2)
(4.2.2)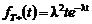 .
.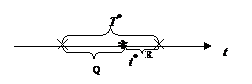
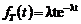 . Возникающий, так называемый, парадокс инспекции разрешается довольно просто. В качестве наводящих рассуждений рассмотрим модельный пример. Пусть интервал между событиями (неперекрывающиеся отрезки на оси t) может принимать только два возможных значения
. Возникающий, так называемый, парадокс инспекции разрешается довольно просто. В качестве наводящих рассуждений рассмотрим модельный пример. Пусть интервал между событиями (неперекрывающиеся отрезки на оси t) может принимать только два возможных значения 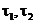 с вероятностями р1 и р2=1-р соответственно. На ось t бросается случайная точка t*. Требуется найти закон распределения интервала, в который попала брошенная точка. В данной постановке применима формула Байеса. Гипотезы
с вероятностями р1 и р2=1-р соответственно. На ось t бросается случайная точка t*. Требуется найти закон распределения интервала, в который попала брошенная точка. В данной постановке применима формула Байеса. Гипотезы 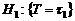 и
и 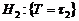 имеют априорные маргинальные (безусловные) вероятности
имеют априорные маргинальные (безусловные) вероятности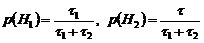 , (4.2.3)
, (4.2.3)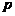 и
и 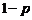 есть условные априорные вероятности. Искомые апостериорные вероятности после сокращения полученных дробей, составят:
есть условные априорные вероятности. Искомые апостериорные вероятности после сокращения полученных дробей, составят: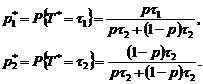 (4.2.4)
(4.2.4)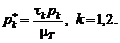 (4.2.5)
(4.2.5)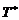 составит
составит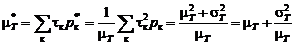 . (4.2.6)
. (4.2.6)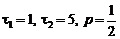 . Результаты сведены в табл. 4.2.1.
. Результаты сведены в табл. 4.2.1.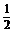
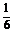
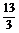
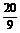
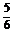
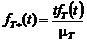 , (4.2.7)
, (4.2.7)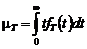 .
. 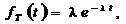
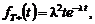
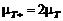 . Таким образом, случайная точка (инспектор) изменяет закон распределения покрывающего ее интервала в сторону больших значений. Прежде чем этот парадокс инспекции был разрешен в 30-40 гг. прошлого века, он изрядно попортил нервы специалистам, занимающимся испытаниями на надежность.
. Таким образом, случайная точка (инспектор) изменяет закон распределения покрывающего ее интервала в сторону больших значений. Прежде чем этот парадокс инспекции был разрешен в 30-40 гг. прошлого века, он изрядно попортил нервы специалистам, занимающимся испытаниями на надежность.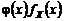 , где X – положительно-определенная СВ, а
, где X – положительно-определенная СВ, а 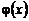 - произвольная положительно‑определенная функция без особенностей. Проделав цепочку рассуждений, аналогичную только что рассмотренной, получим
- произвольная положительно‑определенная функция без особенностей. Проделав цепочку рассуждений, аналогичную только что рассмотренной, получим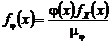 , (4.2.8)
, (4.2.8)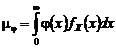 . (4.2.9)
. (4.2.9) 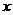 среди попавших в поле микроскопа с большой глубиной резкости), частицы которого без большой натяжки можно считать шарами. Для пересчета ПР массогранулометрического спектра (удельной доли массы, содержащейся в частицах диаметром
среди попавших в поле микроскопа с большой глубиной резкости), частицы которого без большой натяжки можно считать шарами. Для пересчета ПР массогранулометрического спектра (удельной доли массы, содержащейся в частицах диаметром 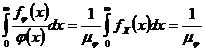 . (4.2.10)
. (4.2.10)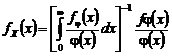 . (4.2.11)
. (4.2.11)