
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Очереди и задачи обслуживания1.Рассмотрим несколько иную логическую схему вывода соотношений (4.1.12) – (4.1.15). Определим процесс пуассона с помощью следующей конструктивной схемы. Обозначим Обозначим для большего удобства записи последующих соотношений:
откуда получаем разностное соотношение: В пределе при h®0 (4.3.2) преобразуется в систему рекуррентных дифференциальных уравнений:
При n=0, полагая в (4.3.3)
решением которого, удовлетворяющим условию
что соответствует формуле общего члена (4.1.13) при k=0. Подставляя (4.3.5) в (4.3.3), находим Вывод (4.3.1) – (4.3.3) предпочтительнее, чем используемый в п.4.1, с той точки зрения, что естественным образом допускает дальнейшие обобщения. Процесс Пуассона можно рассматривать как простейший частный случай процесса чистого размножения. Его более общей стационарной формой является ситуация, когда l зависит от n. В этом случае система дифференциальных уравнений (4.3.3), (4.3.4.) преобразуется к виду  В соответствии с такой вероятностной схемой протекают процессы последовательных атомных радиоактивных превращений, накопления повреждений при эксплуатации технического объекта и т.д. 2. В зависимости от специфики реального процесса структура (4.3.6) может варьироваться, например, наличием терминального (поглощающего) состояния с номером m, так, что для всех n>m Начальным состоянием может быть необязательно нулевое, а произвольное n=k, такое, что Pk(0)=1, а для всех n¹k Pn(0)=0. Следующим обобщением, более содержательным с точки зрения практических приложений задачи массового обслуживания, моделирования очередей и т.д., является ситуация, когда количество событий (объектов) с течением времени может не только возрастать, но и уменьшаться, так называемые процессы размножения и гибели. Система дифференциальных уравнений (4.3.6) в такой ситуации преобразуется к виду
где wn – величина, обратная средней продолжительности жизни в n-м поколении. Система (4.3.7) имеет предельное (при t®¥) стационарное решение. Приравняв к нулю левые части (4.3.7), находим стационарные вероятности перехода: 3. Прежде, чем переходить к содержательному рассмотрению приложений схемы процесса размножения и гибели, рассмотрим промежуточную ситуацию, когда продолжительность «жизни» является детерминированной величиной. В наиболее наглядной (естественной) интерпретации суть рассматриваемой проблемы такова. При пересечении нерегулируемого перекрестка по второстепенной дороге необходимо дождаться «окна» длительностью t между автомобилями, движущимися по главной дороге. Каков будет закон распределения и числовые характеристики СВ Т* – времени ожидания на переезде «check time», если поток автомобилей на главной дороге образуется СВ Т – интервалом между последовательными прибытиями (пересечениями) с показательным законом распределения:
В другой интерпретации пуассоновский показательный поток образуется последовательными сбоями компьютера. Время, необходимое для решения задачи при безаварийной работе – t. Если при сбое происходит сброс программы, то время решения имеет закон распределения, подобный первому случаю. Единственным отличием будет сдвиг вправо по оси t на величину t. Аналогичная ситуация имеет место при работе счетчика радиоактивных частиц (первых моделей), последовательных разладках технологической линии и т.п. Далее будем рассматривать естественную интерпретацию «check time». Первое очевидное заключение состоит в том, что Т* является комбинированной СВ, непрерывной справа от точки t=0 и с квантом в точке t=0. Следующее заключение состоит в том, что при случайном начале отсчета (момент появления на переезде никак не связан с потоком автомобилей) время ожидания первого события потока имеет тот же закон распределения, что и интервал движения (4.3.9). Данный факт, известный в литературе как «парадокс времени ожидания», был рассмотрен в п.4.2. Таким образом задачy можно переформулировать, совместив начало отсчета с одним из событий потока. Вывод ФР Т* начнем с кванта в нуле:
Функцию распределения
Рассмотрим структуру ряда
где
где
где Рассмотрим последовательность При n=1 вид ПР вполне очевиден:
При n=2 воспользуемся приемом, рассмотренным в п.1.3. и схемой рис. 4.3.1
Рис. 4.3.1. Схема области интегрированиядля вычисления автосвертки в интервале На интервале
Для
После дифференцирования окончательно получим
Для n=3 аналогичным образом получим
Выражение в фигурных скобках представляет собой ПР трехкратной автокомпозиции СВ R(0,
где
Переходя к безразмерным переменным
При больших значениях а для практических расчетов следует перейти к логарифму Вид зависимости (4.3.21) при
Рис.4.3.2. Плотность распределения относительного времени ожидания
Благодаря структуре ряда (4.3.21) для вычисления числовых характеристик достаточно вычислить характеристики исходного распределения, усеченного на отрезке [0,1]. Суммируя полученные ряды, находим:
При больших значениях а имеет место асимптотическое тождество
Рис.4.3.3. Результаты статистического эксперимента по модели «check time»
Пример с ЭВМ позволяет придать задаче другую, более актуальную применительно к теории надежности, интерпретацию. Пусть заявки на станцию техобслуживания, вызовы на телефонную станцию и т.д. образуют пуассоновский поток (нагрузку) с интенсивностью
4. Естественным обобщением задачи check time (в интерпретации с работой ЭВМ) является ситуация, когда время обслуживания является СВ. Далее ограничимся рассмотрением только показательного времени обслуживания. Простейшая задача в естественной (и, исторически, первой) формулировке выглядит следующим образом. Пусть имеется бесконечно большое число телефонных линий, на которые поступает пуассоновская нагрузка с интенсивностью l. Положим, что продолжительность одного разговора есть показательная СВ со средним значением
Для предельных вероятностей (приравняв к нулю производные по времени) получим систему линейных уравнений:
откуда следует Таким образом, предельное распределение числа занятых линий есть распределение Пуассона с параметром В более реалистичной постановке, когда число линий конечно и равно m, нужно рассматривать два случая: 1) при n£m результаты полностью совпадают с (4.3.25), (4.3.26); 2) при n>m дифференциальное уравнение имеет вид
Предельные вероятности для n>m составят
и образуется очередь длиной n-m. Сумма ряда 5. Небольшое изменение в вероятностной схеме приводит к «шведской» модели обслуживания автоматов (наиболее полные результаты по данной проблеме были получены Эрлангом и, впоследствии, Пальмом). Пусть m автоматов (станков) подчиняются показательному закону функционирования со средним периодом нормальной работы чиком, а время обслуживания подчиняется показательному закону со средним значением Вероятности распределения числа простаивающих автоматов Pn(t), n=0,1,…, m, будут решением системы дифференциальных уравнений (4.3.7) с коэффициентами:
Для предельных при t®¥ вероятностей получим систему линейных уравнений:
откуда находим
Члены ряда (4.3.31) можно интерпретировать следующим образом. Вероятность р0 соответствует ситуации, когда все m автоматов не требуют обслуживания. Вероятность рn при n³2 соответствует тому, что n автоматов простаивают, причем обслуживается только один, а n–1 стоят в очереди на обслуживание. Средняя длина очереди, определяющая эффективность, а точнее говоря, сверхнормативные издержки на данном производственном участке, составит Собственно «обслуживание по-шведски» заключается в «бригадном» методе, когда m автоматов обслуживаются r (r<m) наладчиками. В этом случае, как впервые установил Пальм, при аналогичной нагрузке на одного наладчика Коэффициенты системы уровней (4.3.7) при таком варианте вероятностной схемы будут определяться следующим образом: Для предельных при t®¥ вероятностей получаем систему линейных рекуррентных уравнений:
Оставшаяся неопределенной величина p0, находится из условия нормировки:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 341. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
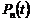 вероятность того, что в течение интервала времени (0,t) произойдет ровно n событий и рассмотрим два смежных интервала (0,t) и (t,t+h), где h=
вероятность того, что в течение интервала времени (0,t) произойдет ровно n событий и рассмотрим два смежных интервала (0,t) и (t,t+h), где h=  . Исходные постулаты Пуассона заключаются в том, что условная вероятность осуществления одного события в интервале (t,t+h) не зависит от t и равна
. Исходные постулаты Пуассона заключаются в том, что условная вероятность осуществления одного события в интервале (t,t+h) не зависит от t и равна 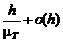 , а вероятность осуществления более чем одного события есть величина высшего порядка малости
, а вероятность осуществления более чем одного события есть величина высшего порядка малости  .
. . Тогда для
. Тогда для  при n≥1, учитывая, что n событий в интервале (0,t+h) могут осуществляться двумя альтернативными способами: 1) n событий за время (0,t) и ни одного – за время (t,t+h) с вероятностью
при n≥1, учитывая, что n событий в интервале (0,t+h) могут осуществляться двумя альтернативными способами: 1) n событий за время (0,t) и ни одного – за время (t,t+h) с вероятностью  ; 2)n-1 событий за время (0;t) и одно – за время (t,t+h) с вероятностью
; 2)n-1 событий за время (0;t) и одно – за время (t,t+h) с вероятностью  , по формуле полной вероятности будем иметь:
, по формуле полной вероятности будем иметь: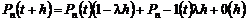 , (4.3.1)
, (4.3.1) . (4.3.2)
. (4.3.2) (4.3.3)
(4.3.3) , получаем однородное уравнение
, получаем однородное уравнение , (4.3.4)
, (4.3.4) , будет
, будет  , (4.3.5)
, (4.3.5) и все последующие члены ряда (4.1.13).
и все последующие члены ряда (4.1.13). (4.3.6)
(4.3.6) .
. (4.3.7)
(4.3.7) . (4.3.8)
. (4.3.8)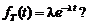 (4.3.9)
(4.3.9) (4.3.10)
(4.3.10) при t>0 будем искать, разлагая в полную группу по числу пропущенных автомобилей:
при t>0 будем искать, разлагая в полную группу по числу пропущенных автомобилей: (4.3.11)
(4.3.11) более детально. При n=1 получим
более детально. При n=1 получим (4.3.12)
(4.3.12) - время от начала отсчета до первой машины,
- время от начала отсчета до первой машины,  - интервал между первой и второй. Для n=2 будем иметь
- интервал между первой и второй. Для n=2 будем иметь (4.3.13)
(4.3.13) -сумма двух независимых исходных СВ, усеченных на отрезке
-сумма двух независимых исходных СВ, усеченных на отрезке  . Продолжив аналогичные рассуждения, получим ПР Т* в следующем виде:
. Продолжив аналогичные рассуждения, получим ПР Т* в следующем виде: (4.3.14)
(4.3.14) - n-кратная автокомпозиция СВ Т, усеченной на отрезке
- n-кратная автокомпозиция СВ Т, усеченной на отрезке  .
. , (4.3.15)
, (4.3.15)

 ПР составит
ПР составит . (4.3.16)
. (4.3.16) сначала найдем ФР, используя рис.4.3.1:
сначала найдем ФР, используя рис.4.3.1:
 (4.3.17)
(4.3.17) (4.3.18)
(4.3.18) ). Таким образом, по индукции получаем формулу общего члена
). Таким образом, по индукции получаем формулу общего члена 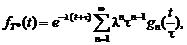 (4.3.19)
(4.3.19)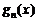 - ПР автокомпозиции СВ R(0,1), рассмотренная в п.1.3;
- ПР автокомпозиции СВ R(0,1), рассмотренная в п.1.3;
 (4.3.20)
(4.3.20) ,
,  , получим
, получим . (4.3.21)
. (4.3.21) .
. приведен на рис. 4.3.2.
приведен на рис. 4.3.2.
 (4.3.22)
(4.3.22) , что эквивалентно пуассоновской асимптотике с параметром
, что эквивалентно пуассоновской асимптотике с параметром  . В свою очередь, преобразование
. В свою очередь, преобразование  будет иметь стандартную нормальную асимптотику
будет иметь стандартную нормальную асимптотику 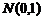 . Полученное решение соответствует первой интерпретации «check time». На рис. 4.3.3 приведены результаты статистического моделирования методом Монте-Карло.
. Полученное решение соответствует первой интерпретации «check time». На рис. 4.3.3 приведены результаты статистического моделирования методом Монте-Карло.
 . Если время обработки одной заявки фиксировано и равно
. Если время обработки одной заявки фиксировано и равно  . (4.3.23)
. (4.3.23) . Тогда, интерпретируя n как количество занятых линий, вероятности Pn(t) находим из системы уравнений (4.3.7), подставляя
. Тогда, интерпретируя n как количество занятых линий, вероятности Pn(t) находим из системы уравнений (4.3.7), подставляя . (4.3.24)
. (4.3.24) (4.3.25)
(4.3.25) . (4.3.26)
. (4.3.26)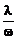 .
. (4.3.27)
(4.3.27) , (4.3.28)
, (4.3.28) при
при  расходится, что означает неограниченное удлинение очереди (как и в модели check time).
расходится, что означает неограниченное удлинение очереди (как и в модели check time). . Положим, что все m автоматов обслуживаются одним налад
. Положим, что все m автоматов обслуживаются одним налад
 (4.3.29)
(4.3.29)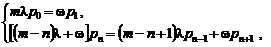 (4.3.30)
(4.3.30) (4.3.31)
(4.3.31) (4.3.32)
(4.3.32) достигается существенное снижение простоя автоматов.
достигается существенное снижение простоя автоматов. (4.3.33)
(4.3.33) (4.3.34)
(4.3.34)