
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интерполяционный многочлен ЛагранжаНа отрезке [a,b] в узлах интерполяции х0, х1,…, хn задается функция f(x) своими n + 1 значениями у0 = f(x0), …, yn=f(xn) . Требуется построить многочлен L(х), совпадающий в узлах интерполяции х0, …, хn со значениями заданной функции: L(x0) = y0, …, L(xn) = yn , где h = xi+1 – xi ¹ const – шаг интерполяции. Представим многочлен
где ai (i = 0, 1 , 2, …, n) неизвестные постоянные коэффициенты, которые нам необходимо найти. Пусть Ln(x) в узлах интерполяции х0, х1, …, хn принимает значения Ln(x0) = уn . Тогда в узле интерполяции х0 имеем
…
Запишем это в виде системы n + 1 уравнений с n + 1 неизвестным а0 , а1, а2, …, аn .
где xi и yi (i = 0, 1,…, n) – табличные значения аргумента и функции. Находим значения неизвестных, как
где
Если
Перепишем этот многочлен в другой форме
где
удовлетворяет следующим условиям:
В точках x0, x1, … , xi-1, xi+1 , … , xn функция Qi(x) обращается в ноль, а в точке хi равна 1 . Окончательно получаем
Этот многочлен называется интерполяционным многочленом Лагранжа
где х0, х1,…. хn – узлы интерполяции, а х – значение аргумента, для которого определяется приближенное значение по интерполяционной формуле Лагранжа. Обозначим произведение элементов первой строки через R0:
В общем виде произведение элементов i строки
Дополнительно вычислим произведение элементов, расположенных на главной диагонали
тогда интерполяционный многочлен Лагранжа можно переписать в виде 
Интерполяционная формула Лагранжа заметно упрощается, если узлы интерполяции равноотстоящие, т.е. Обозначим q = (x - x0)/h , тогда
Введем обозначения:
…
тогда
Заметим, что часть произведения в знаменателе равна
а другая
Умножив числитель и знаменатель правой части последнего равенства на (-1)n-i(q - i), получим
где
Интерполяционный многочлен Лагранжа для равноотстоящих узлов интерполяции теперь можно записать в виде
|
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 266. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
, ,
, ,
, .
.
 ;
;  ;
;  ; … ;
; … ;  ,
, – определитель системы.
– определитель системы.
 .
. ,
,
 .
.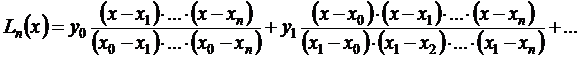
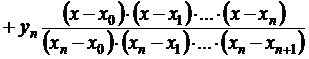 .
. ,
, .
.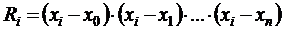 .
. ,
, .
. .
. .
.


 ,
, .
. ,
, .
. ,
, .
.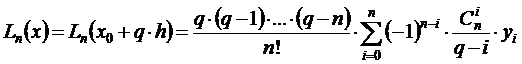 .
.