
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Оценка погрешностей интерполяционных формул Ньютона
Оценка погрешности для интерполяционной формулы Лагранжа:
Если все узлы интерполяции равноотстоящие, то, введя шаг
где Аналогичным образом, для второй интерполяционной формулы Ньютона с равноотстоящими узлами интерполяции, полагая
где
ЛЕКЦИЯ 8. ЛИНЕЙНОЕ ИНТЕРПОЛИРОВАНИЕ
В тех случаях, когда нет необходимости в отыскании приближенного аналитического выражения функции y = f(x), заданной таблично, требуется лишь определить значение функции в точке, отличной от узла интерполяции, удобно использовать последовательную линейную интерполяцию по Эйткину.
Интерполирование по Эйткину Вычисление значения функции в точке, отличной от узлов интерполяции, начинается с вовлечения в счет двух узлов интерполяции с последующим включением в схему новых узлов интерполяции. Пусть некоторый интерполяционный многочлен F(x) степени n принимает в узлах интерполяции х0, х1, …, хn значения
Воспользовавшись формулой Лагранжа для случая линейной интерполяции, на отрезке [x0, x1] интерполяционное значение функции можно вычислить по формуле
на отрезке [x1, x2]
и, наконец, на отрезке [x0, x2] по формуле
Далее заменим у0 и у2 в формуле (8.3) соответственно на F0,1(x) и F1,2(x) .
Получим следующее выражение
или
Интерполяция и приближение сплайном 
Для определенности будем говорить о приближении функции f(x) на [0,1]. Разобьем отрезок на части
и обозначим это разбиение через Назовем «сплайном»
при хn-1£ x £ xn удовлетворяющую условиям непрерывности производных до порядка m – 1 в точках х1, …, xn-1:
при Всего имеется в распоряжении Другие уравнения для коэффициентов получают из условия близости сплайна к приближаемой функции и из некоторых дополнительных условий. |
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 273. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.
 и полагая
и полагая  , получим оценку погрешности для первой интерполяционной формулы Ньютона(7.4)
, получим оценку погрешности для первой интерполяционной формулы Ньютона(7.4) ,
, Î отрезку интерполяции [x0, xn].
Î отрезку интерполяции [x0, xn]. , получим оценку погрешности
, получим оценку погрешности .
. ;
;  ; …;
; …;  .
. , (8.1)
, (8.1) , (8.2)
, (8.2) . (8.3)
. (8.3) ,
, .
.
 .
. порядка m функцию, являющуюся многочленом степени m на каждом из отрезков
порядка m функцию, являющуюся многочленом степени m на каждом из отрезков 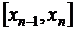 , т.е.
, т.е. ,
, (8.5)
(8.5) .
. неизвестных коэффициентов аnm, и соотношения (8.5) образуют систему из
неизвестных коэффициентов аnm, и соотношения (8.5) образуют систему из  линейных алгебраических уравнений.
линейных алгебраических уравнений.