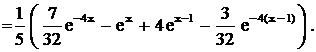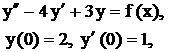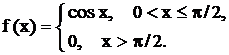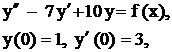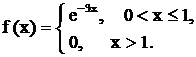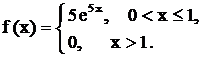Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задача 12. Метод вариации произвольных постоянных, метод Лагранжа.Рассмотрим метод вариации произвольных постоянных для уравнения второго порядка Если известна фундаментальная система решений соответствующего однородного уравнения то общее решение неоднородного уравнения (1) может быть найдено методом вариации постоянных (метод Лагранжа). Общее решение уравнения (2) имеет вид где Решение уравнения (1) будем находить в виде где Решая (5) относительно Из (6) находим где Пример 18. Решить уравнение Решение. Соответствующее однородное уравнение будет Его характеристическое уравнение Общее решение исходного уравнения имеем в виде
Для их нахождения составим систему  Решаем эту систему относительно Интегрируя, находим Подставляя выражения Здесь Упражнения. Решить уравнения. 1) 2) 3) 4) или Решить методом вариации произвольных постоянных следующие уравнения:
Рассмотрим задачу где Пример 19. Решить методом Коши Решение.
Найдем нормированную ф.с.р.:
а) б)
Вычислим интеграл:
Подставим в решение
Задача 13. Решить неоднородные линейные дифференциальные уравнения с правой частью неспециального вида методом Коши.
Задача 14. Решить неоднородные линейные дифференциальные уравнения с разрывной правой частью методом Коши. Пример 20. Решить методом Коши Решение. Составим характеристическое уравнение: Найдем нормированную ф.с.р. а) б) где 1. 2.
Задача 15. По условию задачи составить дифференциальное уравнение и решить его. Дифференциальные уравнения являются математической моделью реальных процессов. При составлении д.у. мы пользуемся законами конкретных наук, таких как физика, химия, биология, экономика. Рассмотрим несколько примеров. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 229. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) , (2),
, (2), , (3)
, (3) – фундаментальная система решений (ф.с.р.),
– фундаментальная система решений (ф.с.р.), – произвольные постоянные.
– произвольные постоянные. , (4)
, (4) – некоторые пока неизвестные функции от х. Для их определения получаем систему
– некоторые пока неизвестные функции от х. Для их определения получаем систему (5)
(5) , получим
, получим (6)
(6) – определитель Вронского.
– определитель Вронского. , т. к.
, т. к.  ,
,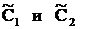 – постоянные интегрирования.
– постоянные интегрирования. .
.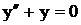 .
. и общее решение имеет вид
и общее решение имеет вид  .
. (*)
(*) – ф. с. р.
– ф. с. р. – неизвестные функции от
– неизвестные функции от 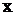 .
.
 :
: .
. .
. в (*), получаем общее решение искомого уравнения
в (*), получаем общее решение искомого уравнения .
. – частное решение исходного уравнения.
– частное решение исходного уравнения. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  ,
, .
. .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
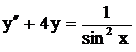 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 , (1)
, (1) , (2)
, (2) , (3)
, (3) – ф.с.р. Если
– ф.с.р. Если  – нормированная ф.с.р., т. е
– нормированная ф.с.р., т. е 

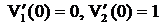 , то решение задачи Коши (1), (2) запишется в виде
, то решение задачи Коши (1), (2) запишется в виде . (4)
. (4) .
. – корни х.у.,
– корни х.у., 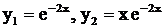 – ф.с.р.
– ф.с.р.
 будем находить в виде линейной комбинации решений
будем находить в виде линейной комбинации решений  и
и  :
: ,
,


 .
.
 .
. .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
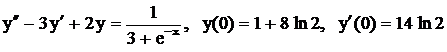 .
.
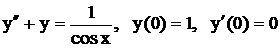 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
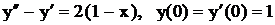 .
.
 .
.




 – ф.с.р.
– ф.с.р. :
: ,
, ;
; ;
; ;
;

 ;
;