
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задача № 1. Уравнения с разделяющимися переменными и приводящиеся к ним.Дифференциальное уравнение
Уравнение Путем деления на произведение
Общий интеграл этого уравнения имеет вид
Замечание. Деление на Дифференциальное уравнение
где уравнение с разделяющимися переменными. Пример 1. Решить уравнение Решение. Разделим обе части уравнения на произведение Получим уравнение с разделенными переменными. Интегрируя его, найдем После потенцирования получим Откуда Обозначая Получили общий интеграл этого уравнения. Функции Ответ: Пример 2. Найти частное решение уравнения Решение. Имеем Разделяем переменные, для этого обе части уравнения делим на произведение Интегрируя, найдем общий интеграл в качестве производной константы После потенцирования, получим Найдем константу 
Искомое частное решение или решение задачи Коши Ответ: Упражнения. Решить уравнения 1. 2. 3. 4. Решить уравнения с разделяющимися переменными:
Задача 2. Однородные дифференциальные уравнения. Дифференциальное уравнение (д.у.) Называется однородным д.у. относительно
функция нулевого измерения. Однородное д.у. всегда можно представить в виде Введя новую искомую функцию
Пример 3. Решить уравнение Решение. Запишем уравнение в виде Разделяя переменные, будем иметь Отсюда интегрированием находим
Ответ: Упражнения. Решить уравнения 1. 2. 3. 4.
Решить однородные дифференциальные уравнения.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 189. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 называется уравнением с разделенными переменными, его общий интеграл имеет вид
называется уравнением с разделенными переменными, его общий интеграл имеет вид .
. , в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от
, в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от 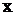 и только от
и только от  называется уравнением с разделяющимися переменными.
называется уравнением с разделяющимися переменными. оно приводится к уравнению с разделенными переменными:
оно приводится к уравнению с разделенными переменными: .
. .
. может привести к потере частных решений, обращающих в ноль произведение
может привести к потере частных решений, обращающих в ноль произведение  ,
, - постоянные, заменой переменных
- постоянные, заменой переменных  преобразуется в
преобразуется в

 .
.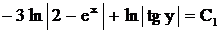 .
. или
или 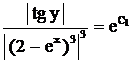 .
. .
. , будем иметь
, будем иметь 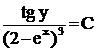 или
или  .
. ,
,  и
и  - являются частными решениями.
- являются частными решениями. - общий интеграл.
- общий интеграл. , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  .
. или
или  .
.
 .
.
 взяли
взяли  .
. или
или  - общее решение исходного уравнения.
- общее решение исходного уравнения. ,
,  или
или отсюда
отсюда  .
. .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  или
или  .
. .
.
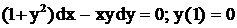 .
.
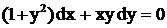 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
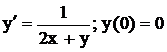 .
.
 .
.
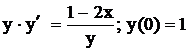 .
.
 .
.
 .
.

 является однородной функцией своих аргументов нулевого измерения. Это значит
является однородной функцией своих аргументов нулевого измерения. Это значит . Например функция
. Например функция  - однородная
- однородная (1)
(1) , уравнение (1) можно привести к уравнению с разделяющимися переменными:
, уравнение (1) можно привести к уравнению с разделяющимися переменными: 
 или
или  переменные разделяются.
переменные разделяются. .
. , разделив на
, разделив на  . Тогда
. Тогда  ,
, 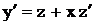 . Получим
. Получим  или
или  .
.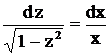 .
.
 или
или , так как
, так как  , то обозначая
, то обозначая  , получим
, получим . Заменяя
. Заменяя  на
на  , будем иметь общий интеграл
, будем иметь общий интеграл , отсюда
, отсюда 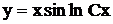 - общее решение.
- общее решение. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Соберем коэффициенты при
. Соберем коэффициенты при 
 . Ответ:
. Ответ:  .
. .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
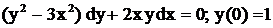 .
.
 .
.
 .
.
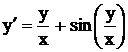 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.