
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные однородные уравнения с постоянными коэффициентами.Рассмотрим дифференциальное уравнение где
которому удовлетворяет Уравнение (3) называется характеристическим уравнением. Пусть Возможны следующие случаи: 1) Тогда фундаментальная система решений уравнения (1) имеет вид 2) Корни характеристического уравнения вещественные, но среди них есть кратные. Пусть, например, Фундаментальная система решений в этом случае имеет вид а общее решение 3) среди корней характеристического уравнения есть комплексные числа. Пусть для определенности А остальные корни вещественные (комплексные корни попарно сопряженные, т. к. по предположению коэффициенты уравнения (3) Фундаментальная система решений имеет вид а общее решение 4) в случае, если  а общее решение
Пример 12. Найти общее решение уравнения Решение. Составляем характеристическое уравнение Находим Пример 13. Найти общее решение уравнения Решение. Характеристическое уравнение имеет вид
Отсюда Пример 14. Решить уравнение Решение. Характеристическое уравнение Общее решение Пример 15. Решить уравнение Решение. Характеристическое уравнение мнимых корней. Общее решение Упражнения. Проинтегрировать следующие однородные линейные уравнения. 1) 2) 3) 4) Решить однородные дифференциальные уравнения с постоянными коэффициентами:
Указание. Воспользоваться формулой извлечения корня
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 198. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
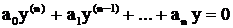 , (1)
, (1)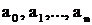 - вещественные постоянные числа. Решение уравнения (1) находим в виде
- вещественные постоянные числа. Решение уравнения (1) находим в виде 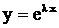 - подстановка Эйлера (2)
- подстановка Эйлера (2)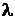 - неизвестная постоянная. Подставляя (2) в (1), получим уравнение
- неизвестная постоянная. Подставляя (2) в (1), получим уравнение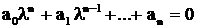 , (3)
, (3)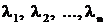 - корни уравнения (3), причем среди них могут быть и кратные.
- корни уравнения (3), причем среди них могут быть и кратные.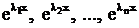 и общим решением искомого уравнения будем
и общим решением искомого уравнения будем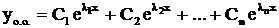 .
.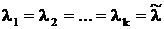 , т. е.
, т. е. 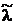 – является
– является  – кратным корнем уравнения (3), а остальные
– кратным корнем уравнения (3), а остальные 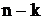 корнем различные.
корнем различные.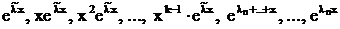 ,
,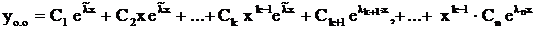 .
.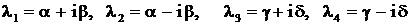 ,
,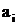 – вещественные).
– вещественные).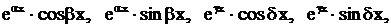

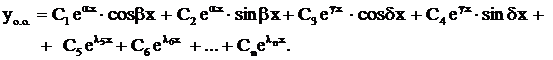
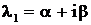 является
является 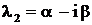 также будет
также будет 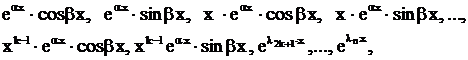
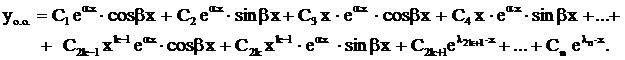
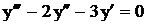 .
.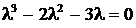 .
.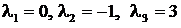 . Так как все они действительные и различные, то общее решение имеет вид
. Так как все они действительные и различные, то общее решение имеет вид 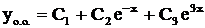 .
.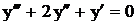 .
.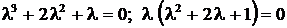 .
.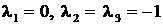 . Корни вещественные, причем один из них
. Корни вещественные, причем один из них 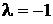 – двукратный, поэтому общее решение имеет вид
– двукратный, поэтому общее решение имеет вид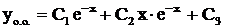 .
.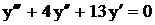 .
.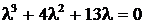 имеет корни
имеет корни 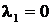 ,
, 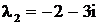 ,
, 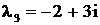 .
.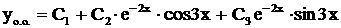 .
.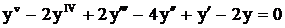 .
.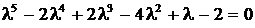 или
или 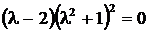 имеет корни
имеет корни 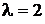 – однократный и
– однократный и 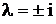 – пара двукратных
– пара двукратных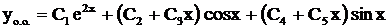 .
.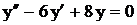 . Ответ:
. Ответ: 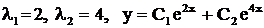 .
.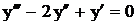 . Ответ:
. Ответ: 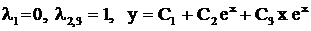 .
.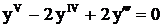 . Ответ:
. Ответ: 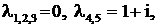
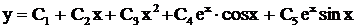 .
. Ответ:
Ответ: 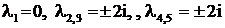 ,
,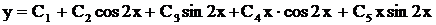 . .
. .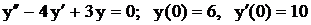 .
.
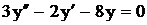 .
.
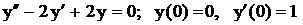 .
.
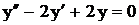 .
.
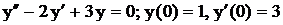 .
.
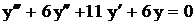 .
.
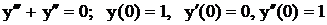 .
.
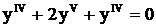 .
.
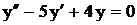 .
.
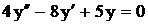 .
.
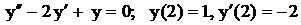 .
.
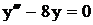 .
.
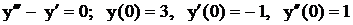 .
.
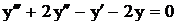 .
.
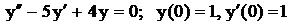 .
.
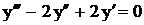 .
.
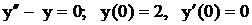 .
.
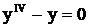 .
.
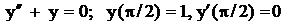 .
.
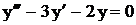 .
.
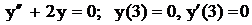 .
.
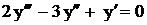 .
.
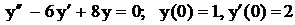 .
.
 .
.
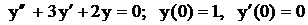 .
.
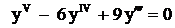 .
.
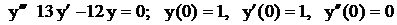 .
.
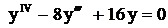 .
.
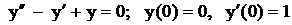 .
.
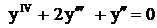 .
.
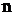 –й степени из комплексного числа
–й степени из комплексного числа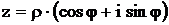 ,
,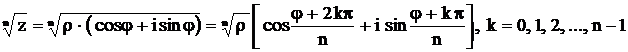 .
.