Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Ориентирование карты по компасу ⇐ ПредыдущаяСтр 9 из 9 Ориентировать карту – это значит расположить её так, чтобы направления линий на карте были параллельными направлениям горизонтальных проекций соответствующих линий местности. При ориентировании карты с помощью компаса необходимо помнить, что ось магнитной стрелки компаса устанавливается в направлении магнитного меридиана. однако на карте имеются только направления истинных меридианов (западная и восточная линии внутренней рамки) и направления, параллельные оси Ох (вертикальные линии километровой сетки). Следовательно, при ориентировании карты с помощью компаса по истинному меридиану необходимо учитывать магнитное склонение δ, а по километровой сетке – склонение δ и сближение меридианов γ; при этом удобно пользоваться схемой взаимного расположения меридианов (истинного, магнитного, осевого), расположенной в левом нижнем углу листа карты.
Ориентирование карты по истинному меридиану.Для ориентирования карты по истинному меридиану компас прикладывают (рис. 17) к западной (или восточной) линии внутренней градусной рамки (истинному меридиану) таким образом, чтобы его диаметр 0-180º был параллелен направлению истинного меридиана, а нуль шкалы компаса направлен на север. Вращая карту вместе с компасом в горизонтальной плоскости, добиваются такого положения, когда северный конец стрелки компаса отклонится от нуля на величину угла, равную склонению магнитной стрелки δ. Если склонение восточное, как на рис. 17, то магнитная стрелка своим северным концом должна отклониться на восток от нуля. При западном склонении северный конец стрелки должен отклониться от нуля градусного кольца компаса на запад.  Ориентирование карты по километровой сетке.при ориентировании карты по километровой сетке компас прикладывают к вертикальной линии километровой сетки (рис. 17) и, вращая карту с компасом в горизонтальной плоскости, добиваются такого положения, чтобы северный конец стрелки отклонился от нуля на угол, равный суммарной поправке за склонение и сближение меридианов, т.е. П = (±δ) – (±γ). В приведённом примере (рис. 17) северный конец стрелки компаса должен отклониться на восток на угол П = (+0º45') – (-0º27') = +1º12'.
Решение задач по карте (или плану), с горизонталями
Определение высот точек по горизонталям.возможны два случая: точка лежит на горизонтали; точка находится между горизонталями. Отметка точки, расположенной на горизонтали, равна отметке этой горизонтали. Если горизонталь не оцифрована, то её отметку находят по оцифровке соседних горизонталей с учетом высоты сечения рельефа. Более общий случай, когда точка находится между двумя горизонталями. Пусть точка М (рис. 18, а), отметку которой требуется определить, находится между горизонталями с отметками 180м и 185м. Через точку М проводят прямую АВ, перпендикулярную горизонталям. На плане измеряют заложение d = АВ и отрезок от младшей горизонтали до точки М – l = АМ. Как видно из вертикального разреза по линии АВ
отсюда
тогда
Рис.18 Определение высотных отметок точек по горизонталям плана или карты: а – точка расположенная между двумя разноимёнными горизонталями на плане или карте; б – профиль по АВ; в – точка расположена между одноименными горизонталями.
Для приведенного на рис. 18, а примера
НМ = 180м +
заложение d и расстояние l измеряются масштабной линейкой. Если точка расположена между горизонталями с одинаковыми отметками (точка А на рис. 18, в) либо внутри замкнутой горизонтали (точка В), то её отметку можно определить лишь приближенно. Считают что отметка этой точки будет отличаться от высоты горизонтали на половину высоты сечения рельефа. Например: если высота сечения h=5м, НА=175-2,5=172,5м; НВ=185+2,5=187,5м. поэтому отметки характерных точек рельефа (вершины холма, дно котлована и т.п.), полученные из измерений на местности, выписывают на планах и картах.
Определение уклона и крутизны ската.под направлением ската понимают направление наибольшей крутизны, которая является нормалью к двум соседним горизонталям на карте. Зная высоту сечения h и измерив заложение ската d с учетом масштаба, можно вычислить уклон линии по формуле:
Например: h = 5м, d = 1,3см., масштаб рассматриваемой карты 1:25000
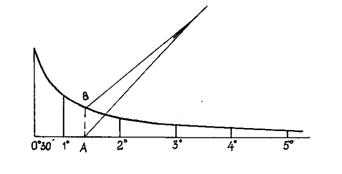
чтобы избежать расчетов при определении уклонов и крутизны скатов по плану или карте, пользуются специальными графиками, называемыми графиками заложений (рис. 19).
Рис. 19 График заложений (масштаб 1:25000, высота сечения h = 5м)
Пусть требуется определить угол наклона ската δ между точками А и В. Для этого берём раствором циркуля заложение d = АВ с плана (карты) и переносим его на график заложений (рис. 19) так, чтобы отрезок АВ оказался параллельным линиям графика, одна точка циркуля располагалась на горизонтальной линии, другая на кривой. Значение крутизны ската определяют пользуясь оцифровкой горизонтальной шкалы графика. В рассматриваемом примере (рис. 19) крутизна ската δ = 1,4º, уклон i = tg1,4º = 0,025. Графики заложений приводятся за оформительской рамкой (рис. 12); они рассчитываются и строятся соответственно сечению рельефа и масштабу плана или карты.
Проектирование трассы с заданным уклоном.при проектировании железных и шоссейных дорог, каналов и других линейных объектов возникает необходимость наметить на карте (плане) трассу будущего сооружения с заданным уклоном. Пусть на карте масштаба 1:25000 (рис. 20) требуется наметить трассу между точками С и Д с уклоном не более i = 0,020, если высота сечения h = 5м. Рассчитывают заложение, соответствующее заданному уклону i и высоте сечения рельефа h, используя формулу (23):
Рис. 20 проектирование трассы с заданным уклоном
и выражают его в масштабе карты
где М – знаменатель численного масштаба. Величину заложения d' можно также определить по графику заложений. Раствором циркуля - измерителя равным d' = 1см, из точки С засекают соседнюю горизонталь и получают точку 1; из точки 1 тем же раствором засекают следующую горизонталь, получая точку 2, и т.д. Соединив полученные точки, получают линию с заданным уклоном. Если расстояние между горизонталями в некоторых частях карты оказываются больше заложения d', то линию откладывают по направлению кратчайшего расстояния между ними. Составляется несколько вариантов трассы между точками С и Д. За окончательный вариант трассы между точками С и Д принимается тот, который имеет меньше углов поворота и минимальную длину.
Измерение площадей по плану или карте площади участков местности по плану или карте могут быть измерены графическим, аналитическим и механическим способами. Графический способ определения площадей.Для определения площадей небольших участков по плану или карте применяется графический способ с разбивкой участка на геометрические фигуры либо с помощью палеток. В первом случае искомую площадь небольшого (до 10 - 15см2 на плане или карте) участка разбивают на простейшие геометрические фигуры: треугольники, прямоугольники, трапеции. Затем на плане (карте) измеряют соответствующие элементы фигур (длины оснований и высот) и по геометрическим формулам вычисляют площади этих фигур. Площадь всего участка определится как сумма площадей отдельных фигур. Поскольку графическая погрешность линейных измерений на плане ли карте (tгр = 0,2 мм) не зависит от длины отрезка, то относительная погрешность короткой линии будет больше, чем длинной. Поэтому участок следует разбивать на фигуры больших размеров с примерно одинаковыми длинами оснований и высот. Для контроля и повышения точности площадь участка определяют дважды, разбивая участок на другие геометрические фигуры. Относительная ошибка двух измерений не должна превышать 1:200. Определение площадей (до 2 - 3см2) участков с резко выраженными криволинейными границами рекомендуется производить с помощью квадратной палетки (рис.21, а).
Рис. 21 Способы определения площадей: а – квадратной палеткой; б –палеткой с параллельными линиями; в – аналитический способ определения площади.
Палетка – лист прозрачной основы, например, кальки, на которую нанесена сеть квадратов со стороной 1 - 5мм. Палетку накладывают на план и подсчитывают число полных квадратов N1, расположенных внутри контура участка и число N2 полных квадратов, составляемых из неполных квадратов у границ участка. Площадь измеряемого участка:
S = s (N1+N2), (24) где s –площадь квадрата палетки с учётом масштаба, м2. Для контроля площадь участка измеряют повторно, развернув палетку примерно на 45º. Относительная погрешность определения площади палеткой составляет 1:50-1:100. При определении площадей до 10см2 можно использовать палетку с параллельными линиями (линейную палетку), представляющую собой лист прозрачной основы, на которой через равные промежутки а =(2-5)мм нанесён ряд параллельных линий (рис. 21, б). Палетка накладывается на заданный участок таким образом, чтобы крайние точки 1 и 2 контура разместились посредине между линиями палетки. Площадь фигуры оказывается расчлененной на фигуры, близкие к трапециям. Измеряют средние линии трапеций l1,12, l3,…ln с помощью циркуля-измерителя и масштабной линейки. Площадь фигуры определится по формуле:
Суммарная длина отрезков аналитический способ определения площадей. Если по результатам измерений на плане или карте определены координаты вершин замкнутого многоугольника, то площадь его может быть определена аналитическим способом. Пусть известны прямоугольные координаты вершин треугольника 1-2-3 (рис. 21, в). Опустив из его вершин перпендикуляры на ось ОY, площадь треугольника можно выразить через площади трёх трапеций: I - (1'-1-2-2'), II -(2'-2-3-3') и III - (1'-1-3-3'), т.е. S = SI + SII – SIII. Рассчитаем площади трапеций:
Определим площадь треугольника S:
преобразуем выражение и получим:
или
в общем виде для треугольника
Для многоугольника с числом вершин n и их оцифровке по часовой стрелке формулы в общем виде запишутся так
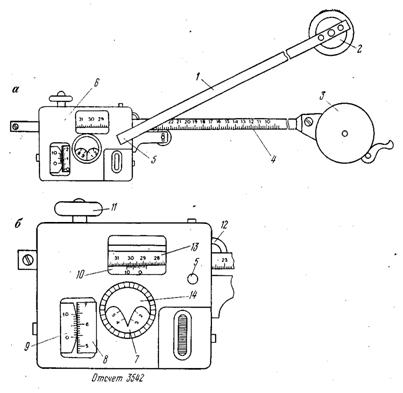
где n – вершина многоугольника, n=1, 2, 3, … Механический способ определения площадей.В инженерной практике для определения площадей по планам и картам применяется механический способ, основанный на использовании специального прибора – планиметра. Наибольшее распространение получили полярные планиметры типов ПП – 2К и ПП – М (рис. 22).
Рис. 22 Полярный планиметр ПП –М: а –общий вид; б –каретка со счётным механизмом.
Полярный планиметр ПП – М (рис. 22, а) состоит из двух рычагов –полюсного 1 и обводного 4. В нижней части груза 2, закреплённого на одном из концов полюсного рычага, имеется игла – полюс планиметра. На втором конце полюсного рычага находится штифт с шарообразной головкой, вставляемой в гнездо 5 каретки 6 обводного рычага. На конце обводного рычага имеется линза 3, на которой нанесена окружность с обводной точкой в центре. Каретка 6 имеет счётный механизм (рис. 22, б), который состоит из счётного колеса 8 и счётчика 7 целых оборотов счётного колеса. Для отсчётов по счётному колесу имеется специальное устройство – верньер 9. при обводе контура участка обводной точкой линзы 3 ободок счётного колеса и ролик 11 катятся или скользят по бумаге; вместе с обводной точкой они образуют три опорные точки планиметра. Отсчёт по планиметру состоит из четырёх цифр: первая – ближайшая к указателю 14 младшая цифра счётчика оборотов (тысячи делений планиметра), вторая и третья цифры – сотни и десятки делений, предшествующие нулевому штриху верньера, четвёрная цифра – номер штриха верньера, совпадающего с ближайшим штрихом счётного колеса (единицы делений). Каретка со счётным механизмом (рис. 22) после ослабления винта 12 может передвигаться вдоль обводного рычага 4, изменяя тем самым его длину. Необходимая длина обводного рычага устанавливается на шкале делений 13, расположенной на его верхней грани, с помощью верньера 10. Перед измерением площади участка план или карта закрепляются на гладкой горизонтальной плоскости. Планиметр устанавливается так, чтобы его полюс располагался вне измеряемого участка, а полюсный и обводной рычаги образовывали примерно прямой угол. Место закрепления полюса выбирают с таким расчётом, чтобы во время обвода фигуры угол между обводным и полюсным рычагами был не менее 30º и не более 150º. Совместив обводную точку планиметра с исходной точкой контура, снимают по счётному механизму начальный отсчёт nН и плавно обводят весь контур по ходу часовой стрелки. Вернувшись в исходную точку, берут конечный отсчёт nК тогда площадь измеряемого участка
S = μ (nК – nН), (28)
где μ – цена деления планиметра, т.е. площадь, соответствующая одному делению планиметра. Большие площади на планах и картах следует измерять по частям. Для этого измеряемую фигуру делят на части плавными слегка изогнутыми линиями. Площади слишком узких, вытянутых фигур (дорог, оврагов, речек и т.п.) измерять планиметром не рекомендуется. Для контроля и повышения точности результатов измерений площадь участка следует измерять не менее четырёх раз: два раза обводя фигуру по часовой стрелке и 2 раза – против хода часовой стрелки. Перед измерением площадей необходимо определить цену деления планиметра μ. Цена деления бывает абсолютной μабс., если она выражена в мм2/дел., и относительной μотн., если она выражена в м2/дел. или га/дел., с учётом масштаба данного плана (карты). Для определения цены деления планиметра выбирают фигуру площадь которой S0 известна (например, один или несколько квадратов километровой сетки карты). Фигуру обводят по контуру четыре раза (два раза по часовой стрелке, два раза против хода часовой стрелки). При каждом обводе берут начальный и конечный отсчёт и вычисляют их разность. Расхождения между значениями разностей не должны превышать при площади фигуры до 200 делений – 2, от 200 до 2000 делений – 3 и свыше 2000 – 4 деления. Если расхождения не превышают допустимых значений, то рассчитывают среднюю разность отсчётов Δnср. и вычисляют цену деления планиметра по формуле:
Рассмотрим пример определения площади фигуры планиметром ПП – М на карте масштаба 1:10000: а) определение цены деления планиметра обводился квадрат километровой сетки (10×10см). Отсчёты по планиметру при обводе по часовой стрелке: n1=5317; n2=6356; n3=7396; при обводке против хода часовой стрелки: n4 =8178; n5=7137; n6=6097. Разности отсчётов: Δn1=6356-5317=1039; Δn2 =7396-6356=1040; При обводе фигуры против хода часовой стрелки отсчёты будут уменьшаться, поэтому: Δn3=8178-7137=1041; Δn4=7137-6097=1040.
Так как разности отсчётов не превышают 3 единицы находим среднюю разность отсчётов
Цену деления планиметра определяем в м2/дел, т.е. учитываем масштаб
карты:
б) определение площади фигуры Отсчёты по планиметру при обводе фигуры по часовой стрелке: n'1=5385; n'2=5463; n'3=5543; против хода часовой стрелки: n'4 =7375; n'5=7297; n'6=7218; Находим разности отсчётов: Δn'1=5463-5385=78; Δn'2 =5543-5463=80; Δn'3=7375-7297=78; Δn'4=7297-7218=79.
S = μ ∙ Δnср .= 961,54 ∙ 78,75 = 75721,2м2
Точность определения площадей полярным планиметром зависит главным образом от размеров обводимой фигуры; чем меньше площадь, тем больше относительная погрешность её определения. Поэтому не рекомендуется измерить с помощью планиметра площадь участков на плане или карте меньше 10 – 12см2. В этом случае они точнее будут измерены графическим способом. При благоприятных условиях измерений относительная погрешность определения площадей с помощью полярного планиметра близка к 1:400.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Курошев Г.Д. Геодезия и топография [Текст]: учебник/ Г.Д. Курошев, Л.Е. Смирнов; под ред. Г.Д. Курошева. –М.: Академия, 2006.
2. Маслов А.В. Геодезия [Текст]: учебник/ А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков; под. ред. А.В. Маслова. – М.: КолоС, 2006.
3. Мехелев Д.Ш. Инженерная геодезия. [Текст]: учебник/ Д.Ш. Мехелев. – М.: Академия, 2006.
4. Поклад Г.Г. Геодезия: учебное пособие для вузов [Текст]: учебник/ Г.Г. Поклад, С.П. Гриднев. – М.: Академический проект, 2007 – 592с. ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
Лабораторная работа 1. РЕЛЬЕФ МЕСТНОСТИ И ЕГО ИЗОБРАЖЕНИЕ НА ТОПОГРАФИЧЕСКИХ ПЛАНАХ
Лабораторная работа 2. ПРЯМАЯ И ОБРАТНАЯ ГЕОДЕЗИЧЕСКИЕ ЗАДАЧИ
Лабораторная работа 3. МАСШТАБЫ ПЛАНОВ И КАРТ И ИХ ТОЧНОСТЬ
Лабораторная работа 4. РЕШЕНИЕ ИНЖЕНЕРНО-ТЕХНИЧЕСКИХ ЗАДАЧ ПО ТОПОГРАФИЧЕСКОЙ КАРТЕ
библиографический список |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 667. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
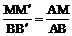 или
или 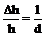 ,
, 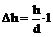 . (21)
. (21)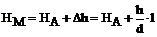 . (22)
. (22)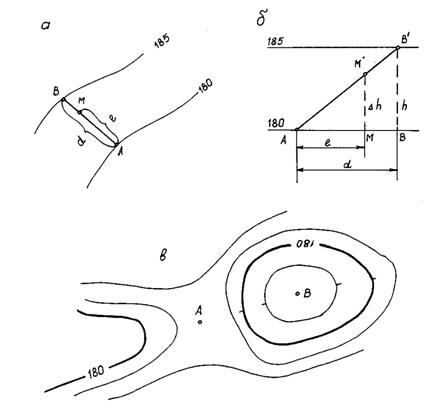
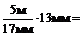 183,8м;
183,8м; 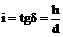 . (23)
. (23)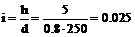 ;
; 
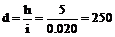 м.
м. 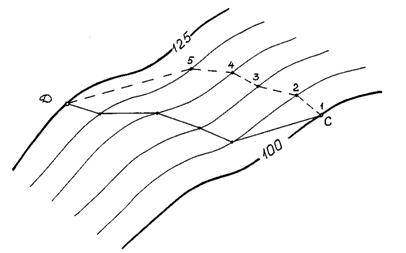
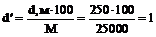 см,
см, 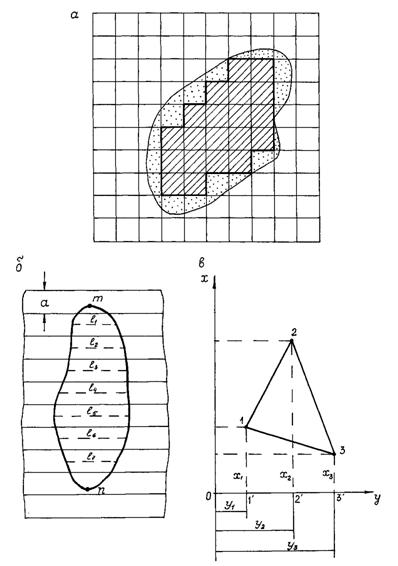
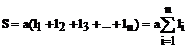 (25)
(25)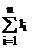 может быть замерена с помощью курвиметра. Для контроля измеряют площадь при втором положении палетки, развернув её на 60º - 90º.
может быть замерена с помощью курвиметра. Для контроля измеряют площадь при втором положении палетки, развернув её на 60º - 90º.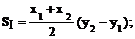
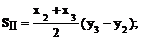
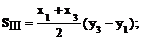
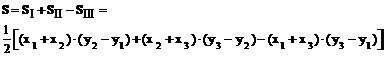
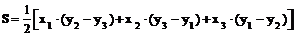
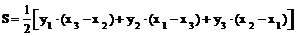
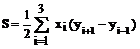 ;
; 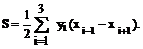 (26)
(26)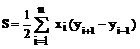 ;
; 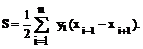 (27)
(27)
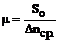 (29)
(29)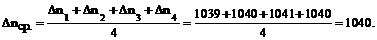
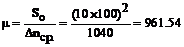 м2;
м2;