
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Прямая и обратная геодезические задачи
Цель работы: научиться решать прямые и обратные геодезические задачи.
Краткие теоретические сведения Обработка результатов полевых измерений на местности, проводимая при составлении планов, решении ряда задач при проектировании сооружений и геодезической подготовке данных для выноса проекта в натуру, связаны с решением прямой и обратной геодезической задач.
Прямая геодезическая задача Сущность прямой геодезической задачи заключается в следующем: известны координаты одной из точек, например, точки А (хА, уА), дирекционный угол стороны АВ – αАВ и её горизонтальная проекция dАВ (рис. 7). Требуется определить координаты второй точки В (хВ, уВ).

Рис. 7. схема к решению прямой и обратной геодезических задач
Проведя через точки А и В линии, параллельные координатным осям, получим прямоугольный треугольник АВС, в котором известны гипотенуза dАВ и острый угол rАВ= αАВ. Катеты этого треугольника есть приращения координат Δх и Δу, которые могут быть получены по формулам:
Δх=± dАВ·cos rАВ= dАВ·cos αАВ; Δу=± dАВ·sinrАВ= dАВ·sinr αАВ. (2)
Если расчёты Δх и Δу выполняются по румбам, необходимо правильно выбрать знаки приращений координат. Они будут зависеть от четверти, в которой находится данное направление, четверть зависит от значения дирекционного угла (табл. 2).
Таблица 2 Соотношения между дирекционными углами и румбами
 контроль вычисления приращений координат:
координаты искомой точки В определяются по формулам:
хВ=хА+Δх; уВ=уА+Δу. (4)
приращения координат и координаты искомой точки вычисляются с точностью, соответствующей точности измерения горизонтальной длины линии. Этим способом можно найти координаты любого числа точек по правилу, вытекающему из формулы (4): координаты последующей точки равны координатам предыдущей точки плюс соответствующее приращение со своим знаком.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 717. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||
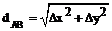 . (3)
. (3)