
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обратная геодезическая задачаСущность обратной геодезической задачи: по известным координатам точек А(хА, уА) и В(хВ, уВ) требуется определить дирекционный угол направления αАВ и горизонтальное приложение (горизонтальную проекцию) стороны dАВ. Согласно рис. 7 приращения координат можно вычислить по формулам:
Δх = хВ - хА; Δу = уВ - уА. (5)
При определении приращений координат Δх и Δу необходимо помнить, что если вычисляется дирекционный угол направления АВ (αАВ), то из координат конечной точки вычисляют координату начальной; при определении αВА – наоборот из координаты точки А вычитают координату точки В. Исходя из этого правила определяются знаки приращений координат – «плюс» или «минус». По найденным значениям приращений координат Δх и Δу в прямоугольном треугольнике, вычисляют табличный угол:
отсюда
По знакам приращений координат Δх и Δу определяют, в какой четверти находится данное направление, по четверти определяют дирекционный угол направления (см. табл. 2). Зная дирекционный угол направления и приращения координат, определяют горизонтальное приложение стороны
Значение горизонтального проложения стороны необходимо определить по всем трём формулам; сходимость результатов служит надёжным контролем решения задачи.
Примеры решения прямой и обратной геодезических задач
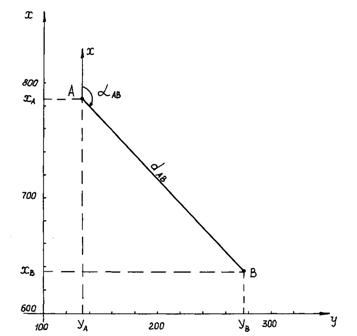
пример 1.Даны: координаты точки А (хА=1035,06м, уА=8472,34м), дирекционный угол направления αАВ=224º38'45", горизонтальное расстояние между точками dАВ=146,35м. Требуется вычислить координаты точки В (хВ, уВ). Строим схему в произвольном масштабе (рис.8).  Вычисляем приращения координат:
Δх=dАВ·cosαАВ=146,35·cos224º38'45"=146,35·(-0,711464)=-104,12м; Δу= dАВ·sinαАВ=146,35·sin224º38'45"=146,35·(-0,702722)=-102,84м;
Осуществляем контроль:
Рис. 8. Схема к примеру решения прямой геодезической задачи
Вычисляем координаты точки В:
хВ=хА+Δх=1035,06+(-104,12)=930,94м; уВ=уА+Δу=8472,34+(-102,84)=8369,50м.
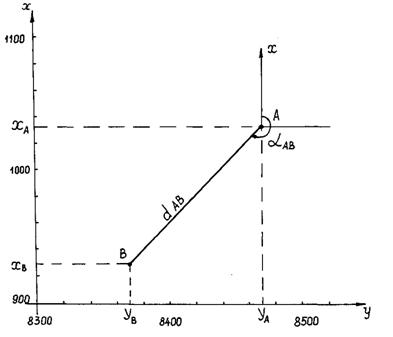
Пример 2.Даны координаты точки А (хА=786,44м, уА=134,29м); координаты точки В (хВ=634,82м, уВ=274,98м). определить дирекционный угол направления АВ - αАВ и горизонтальную проекцию отрезка АВ - dАВ. По исходным данным в произвольном масштабе наносим на план точки А и В (рис. 9).
Рис. 9. Схема к примеру решения прямой геодезической задачи
Вычисляем приращения координат:
Δх = хВ - хА = 634,82 - 786,44 = - 151,62м; Δу = уВ - уА = 274,98 - 134,29 = + 140,69м.
Вычисляем табличный угол:
отсюда rАВ=42º51'31". По знакам приращений координат +Δу и –Δх направление АВ находится во второй четверти, отсюда
α = 180º - r = 180º - 42º51'31" = 137º08'29".
Горизонтальную проекцию dАВ рассчитываем по трем формулам:
Лабораторная работа 3. Масштабы планов и карт и их точность
Цель работы:изучить масштабы планов и карт и получить практические навыки по их применению.
Краткие теоретические сведения
при составлении планов и карт горизонтальные проекции линий местности уменьшают в определённое число раз в зависимости от требований к точности, предъявляемых к планам и картам. Степень уменьшения горизонтальных проекций линий местности при изображении их на плане или карте называется масштабом. Иными словами, масштаб есть отношение длины отрезка s на плане или карте к горизонтальной проекции соответствующего отрезка S на местности, т.е. s / S –масштаб. Различают численный и графический масштабы.
Численный масштаб Численный масштаб – это правильная дробь, числитель которой есть единица, а знаменатель – число, показывающее, во сколько раз горизонтальные проекции линий местности уменьшены на плане или карте.
где М –знаменатель численного масштаба. Чем больше знаменатель численного масштаба М, тем больше степень уменьшения горизонтальных проекций отрезков местности, тем мельче масштаб плана или карты. В геодезии применяются следующие масштабы: для планов - 1:500, 1:1000, 1:2000, 1:5000; для карт - 1:10000, 1:25000, 1:50000, 1:100000, 1:200000, 1:300000, 1:500000, 1:1000000. Указанные отношения показывают, что горизонтальные проекции линий местности уменьшены на плане соответственно в 500, 1000, 2000, и т.д. раз, т.е. отрезку в 1 см на плане соответствуют на местности длины: 500см или 5м; 1000см или 10м; 2000см или 20м и т.д. На картах ниже подписи численного масштаба, например 1:10000, проводится пояснительный масштаб: «в 1см - 100м». При помощи масштабов можно решать следующие задачи: - по длине горизонтальной проекции линии S на местности определить длину соответствующего отрезка s на плане масштаба - по длине отрезка s на плане масштаба Графический масштаб Для исключения вычислений при решении указанных задач удобнее пользоваться графическими масштабами, к которым относятся линейный и поперечный (трансверсальный) масштабы. Линейным масштабом называется графическое изображение численного масштаба в виде прямой линии с делениями для отсчёта расстояний (рис. 10). Для построения линейного масштаба на прямой линии откладывают ряд отрезков одинаковой длины а (например, а = 2см), называемой основанием линейного масштаба. Крайний левый отрезок делят на 10 равных частей; на правом его конце ставят 0, а не левом – число метров (или километров), которое соответствует основанию в заданном масштабе. Вправо от 0 деления масштаба подписывают значениями соответствующих расстояний на местности. Размерность ставится один раз в правом конце линейного масштаба.
Рис. 10 линейный масштаб
На рис.10 показан линейный масштаб для численного масштаба 1:1000. Основание масштаба а = 20м, Чтобы отложить отрезок на плане, равный 56м, используя линейный масштаб, нужно правую ножку циркуля-измерителя поставить на деление 40, а левую на восьмую чёрточку от 0.Десятые доли малого деления оцениваются на глаз. В связи с этим линейный масштаб во многих случаях не позволяет измерять расстояния с необходимой точностью. При оценке точности нанесения точек на план исходят их физиологических возможностей человеческого глаза различать минимальный отрезок, равный 0,1мм (размер точки, поставленной остро отточенным карандашом, кружок от укола остро отточенной иглы). Отсюда следует, что на плане (карте) в самом благоприятном случае можно изобразить лишь такие горизонтальные проекции линий местности, которым в данном масштабе соответствует отрезок 0,1мм и более. Горизонтальное расстояние на местности, соответствующее 0,1мм (0,01см) на плане, называется предельной точностью масштаба tпр, т.е
Длина отрезка на плане или карте может быть оценена с точностью ±0,2мм. Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,2мм (0,02см) на плане, называется графической точностью масштаба tграф., т.е.
Для повышения точности измерений расстояний на плане или карте применяют поперечный масштаб. Для его построения на отрезке АВ (рис. 11) несколько раз откладывают основание масштаба, равное обычно 2см. В полученных точках восстанавливают перпендикуляры к линии АВ произвольной, но равной длины. Два крайних перпендикуляра делят на m равных частей и через одноимённые точки проводят линии параллельные прямой АВ. Левые нижнее АО и верхнее СД основания делят на n равных частей; точку О нижнего основания соединяют наклонной линией с первой точкой Е верхнего основания СД, а через все остальные точки проводят линии, параллельные ОЕ (трансверсали).
Рис. 11 поперечный масштаб
Наименьшее деление ed поперечного масштаба определится из подобия треугольников
где p – наименьшее деление поперечного масштаба, p = ed. Если основание масштаба а = 2см, а m = n = 10, то имеем нормальный сотенный поперечный масштаб. Выразив наименьшее деление масштаба р в масштабе плана или карты, получим точность поперечного масштаба.
Каждая линия, откладываемая на плане или карте, слагается из трёх частей: - числа целых оснований а, взятых от нулевого перпендикуляра до правой ножки циркуля-измерителя; - числа малых делений – десятых долей основания - сотых долей основания Аналогично можно решать обратную задачу –по длине отрезка на плане или карте определить длину соответствующей линии местности. Рассмотрим несколько примеров.
Примеры решения задач
Пример 1. Измерена горизонтальная длина отрезка местности S =58,6м. Определить с помощью поперечного масштаба (рис.11) соответствующий ему отрезок s на плане масштаба 1:1000. Решение. Основание поперечного масштаба а = 20м, цена наименьшего деления основания Число целых оснований, содержащихся в отрезке местности 58,6:20=2. следовательно правую ножку циркуля-измерителя нужно установить на нижнюю линию поперечного масштаба в точке с цифрой 40. Левая ножка циркуля устанавливается так, чтобы в раствор циркуля-измерителя вошло помимо двух целых оснований ещё k малых делений основания, укладываемых в остатке: 58,6-20×20=18,6м. в нашем случае k=18,6:2=9. То есть левая ножка циркуля устанавливается на нижней горизонтальной линии на 9 делений влево от 0 деления. Остался неотложенный отрезок 18,6-18=0,6м. Этот отрезок 0,6:0,2=3. Перемещаем циркуль-измеритель параллельно самому себе вверх на 3 деления так, чтобы правая его ножка шла по перпендикуляру, а левая по трасверсальной линии. Искомая линия на рис. 11 отмечена точками. Пример 2. На плане масштаба 1:1000 взят в раствор циркуля-измерителя отрезок s. Определить, используя поперечный масштаб, длину отрезка S на местности. На рис. 11 отрезок обозначен крестиками. Решение. Устанавливаем, что число целых оснований равно 3, следовательно 20×3=60м. Находим число малых делений основания, их 4, следовательно 2×4=8м. количество сотых делений основания масштаба -8, следовательно 0,2×8=1,6м. Окончательная длина будет равна сумме найденных нами отрезков: 60+8+1,6=69,6м. Пример 3. С какой точностью можно определить длину линий по плану, если m=n=10, основание а=2см, а численный масштаб равен 1:2000. Решение. По формуле (12) находим:
пример 4. какое основание должен иметь поперечный масштаб, чтобы обеспечить построение линий на плане масштаба 1:2000 с точностью t=0,2м, если m=n=10.
Решение.
поперечный масштаб обычно гравируют на металлических пластинках, которые закрепляют на некоторых геодезических приборах (геодезических транспортирах, масштабных линейках, кипрегелях).
Лабораторная работа 4 |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 2078. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
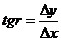 , (6)
, (6)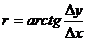 . (7)
. (7)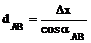 ;
; 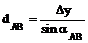 ;
; 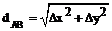 . (8)
. (8)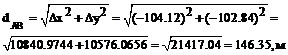
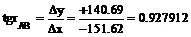 ,
, 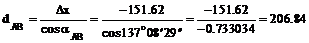 ,м;
,м;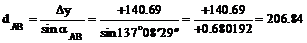 ;
;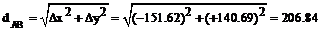 м.
м.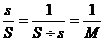 , (9)
, (9)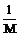 . Например: S=126,8м;
. Например: S=126,8м; 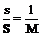 находим
находим 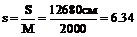 см;
см;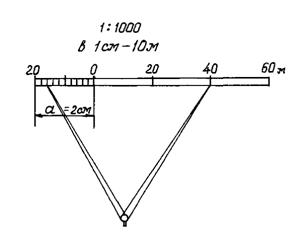
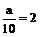 м.
м.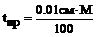 , м (10)
, м (10)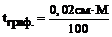 , м (11)
, м (11)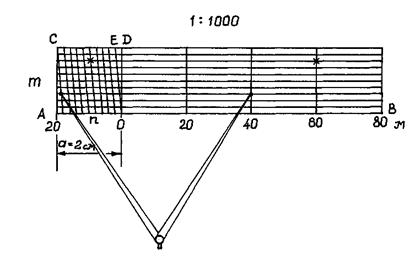
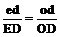 ;
; 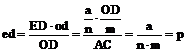 ,
, 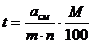 , м (12)
, м (12)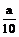 , взятых от нулевого перпендикуляра до левой ножки циркуля-измерителя;
, взятых от нулевого перпендикуляра до левой ножки циркуля-измерителя;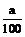 , расположенных между вертикальной линией и трансверсалью.
, расположенных между вертикальной линией и трансверсалью.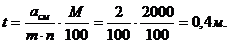
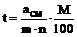 ;
; 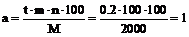 см.
см.