
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лабораторная работа №8. Решение однокритериальной статической задачи в условиях неопределенности при играх с природой с экспериментамиЗадание Используйте придуманную вами задачу разработки управленческого решения. Задайтесь параметрами, которые могут быть в условиях неопределенности. Рассмотрите случай игры с природой с экспериментами и решите задачу. Порядок выполнения работы 1. Из общего числа параметров вашей задачи разработки управленческого решения выберите один, который будет рассматриваться в условиях неопределенности. Согласуйте с преподавателем выбранный вами параметр. 2. На основе анализа ситуации в зависимости от возможных воздействий природы задайтесь 3. Из числа значений случайного параметра
4. Решая задачу с помощью надстройки Поиск решения, определите значение критериальной функции и соответствующие ему решения в предположении, что стратегия природы угадана, то есть мы предполагаем значение параметра 5. Постройте платежную матрицу, заполните ее диагональ значениями 6. Используя полученное решение 7. По формуле (9) рассчитайте средний выигрыш при использовании каждой из  8. Определите величину максимального среднего выигрыша и соответствующую ему стратегию 9. Предположите, что в результате эксперимента вам удалось точно узнать состояние природы. Тогда по формуле (10) вычислите его величину 10. Учитывая, что стратегии природы чередуются с некоторыми вероятностями
11. Задайтесь неким значением 12. Определите результат вычисления неравенства 13. Проведите исследование зависимости целесообразности проведения эксперимента от величины затрат Контрольные вопросы 1. Чем игры с природой с экспериментами отличаются от обычных игр с природой? 2. Что такое априорные данные? 3. Когда целесообразно проведение эксперимента? 4. Что такое единичный эксперимент? 5. Что такое последовательный эксперимент? 6. Как определить наш средний возможный выигрыш после проведения эксперимента? 7. Как рассчитать максимальный средний выигрыш? 8. Что представляет собой решение задачи? 9. В чем отличие методики целесообразности определения эксперимента по критериям Вальда и Сэвиджа? 10. Что такое апостериорные данные? Отчет о работе Подготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, исходные данные, описание проблемы, которая была разрешена. Укажите случайный параметр, взятый в рассмотрение, и обоснуйте его выбор. Приведите обоснование выбора его значений. Представьте платежную матрицу и результаты ее обработки. Укажите предполагаемые затраты на эксперимент и полученные в соответствии с ними решения. Сформулируйте выводы, которые можно сделать по результатам выполненной работы. Пример содержания отчета о выполнении лабораторной работы приведен в приложении Б. Многокритериальные задачи Многокритериальная задача разработки управленческого решения возникает в том случае, когда результат ее решения должен удовлетворять нескольким противоречивым требованиям. В этом случае эффективность решения оценивается совокупностью неких локальных критериев
В методике решении многокритериальных задач дополнительным важным вопросом оказывается выбор принципа оптимальности. Обычно он строится на основе различных способов компромисса между составляющими вектора критериев. Примечание. Под компромиссом понимается соглашение между противоположными, различными мнениями, направлениями и т.д., достигнутое путем взаимных уступок. Компромисс можно отыскать только в том случае, когда возникает противоречие между локальными критериями, то есть когда при изменении решения показатели по одному критерию улучшаются, а по всем другим ухудшаются. Если изменение решения приводит к улучшению показателей по различным критериям, то имеет место ситуация согласия, которая не представляет интереса для решения задачи оптимизации. Определение области компромисса, то есть области допустимых значений решения
При решении практических задач составляющие вектора критериев должны быть приведены к единой размерности или нормализованы. Кроме этого, локальные критерии могут иметь различную степень важности, в связи с чем при выборе оптимального решения это обстоятельство также приходится принимать во внимание. В целом при выборе схемы компромисса приходится решать сложные концептуальные проблемы, что обычно приходится делать с помощью эвристических процедур. На рис. 20 рассмотрена графическая иллюстрация метода отыскания возможного компромисса для двухкритериальной задачи. По осям координат отложены значения локальных критериев
Рис. 20. Область согласия и область компромисса при решении многокритериальных задач В литературе описано несколько распространенных способов выбора компромисса. Наиболее простым является способ скаляризации векторного критерия. В этом случае
и задача разработки управленческого решения из многокритериальной превращается в однокритериальную. Значения весовых коэффициентов
Если скаляризация векторного критерия не представляется возможной, то можно воспользоваться методом, основанном на принципе равенства. В этом случае
то есть наилучшим считается такое решение, при котором достигается равенство локальных критериев. При практической реализации этот метод может оказаться неудобным, поскольку он может выводить решение из области компромисса. Вариантом этого метода является принцип квазиравенства, при реализации которого добиваются не точного равенства, а обеспечения разности между величинами локальных критериев, не превышающих некоторой заданной величины
Еще одним вариантом решения задачи оптимизации является принцип максимина. В этом случае задача оптимизации решается для каждого из локальных критериев, после чего отыскивается такое значение вектора управления в области компромисса, которое обеспечивает максимум наименьшего значения локального критерия
Принцип справедливой уступки предлагают компромисс, при котором суммарный абсолютный или относительный уровень снижения одного или нескольких критериев не превосходит суммарного абсолютного или относительного уровня повышения других критериев. Можно сказать [3], что принцип абсолютной уступки соответствует критерию
а относительной уступки критерию
Принцип выделения главного критерия заключается в том, что среди локальных критериев выделяется один главный, проводится оптимизация по этому критерию, а затем обеспечивается требование, чтобы величины других критериев не были бы меньше некоторых заданных величин. Вариантом этого метода является принцип последовательной уступки, при котором показатели эффективности ранжируются в порядке убывания важности. Далее находят решение обращающее в максимум главный показатель эффективности В целом процедура решения многокритериальной задачи разбиваются на два этапа: собственно оптимизацию в соответствии с одним из ранее рассмотренных методов по каждому из критериев и выбор схемы компромисса между локальными критериями. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 381. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 возможными значениями случайного параметра
возможными значениями случайного параметра  , для которых будет делаться расчет. Каждое значение этого параметра будет определять одну из наших возможных стратегий
, для которых будет делаться расчет. Каждое значение этого параметра будет определять одну из наших возможных стратегий 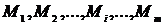
 (
(  ) возможными значениями, которые определяют возможные стратегии природы
) возможными значениями, которые определяют возможные стратегии природы  и вероятности их появления
и вероятности их появления  , обеспечив выполнение условия
, обеспечив выполнение условия .
. , и в результате действий природы он принимает именно такое значение.
, и в результате действий природы он принимает именно такое значение. и отдельно запишите соответствующие нашим стратегиям решения
и отдельно запишите соответствующие нашим стратегиям решения  .
. для каждой строки
для каждой строки  подставляя соответствующее стратегии природы
подставляя соответствующее стратегии природы  значение параметра
значение параметра 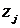 в выражение для критериальной функции рассчитайте остальные элементы платежной матрицы
в выражение для критериальной функции рассчитайте остальные элементы платежной матрицы  .
. наших возможных стратегий.
наших возможных стратегий. .
. для каждой вашей стратегии.
для каждой вашей стратегии. , рассчитайте ваш выигрыш
, рассчитайте ваш выигрыш .
. , определяющим стоимость такого эксперимента, и определите величину среднего выигрыша с учетом эксперимента
, определяющим стоимость такого эксперимента, и определите величину среднего выигрыша с учетом эксперимента  .
. и примите решение о целесообразности или нецелесообразности проведения эксперимента.
и примите решение о целесообразности или нецелесообразности проведения эксперимента. , которые могут различаться своими коэффициентами относительной важности
, которые могут различаться своими коэффициентами относительной важности  . Тогда говорят, что локальные критерии образуют вектор критериев
. Тогда говорят, что локальные критерии образуют вектор критериев  , а коэффициенты вектора важности вектор
, а коэффициенты вектора важности вектор  . Для решения многокритериальной задачи необходимо найти такое значение вектора управления
. Для решения многокритериальной задачи необходимо найти такое значение вектора управления  , которое обеспечит оптимальное значение вектора критериев
, которое обеспечит оптимальное значение вектора критериев
 , для которой имеют место противоречия между составляющими векторного критерия эффективности, само по себе уже представляет достаточно важную задачу, поскольку ее решение существенно уменьшает количество альтернатив. Дальнейший поиск оптимального решения заключается в выборе схемы компромисса, которая соответствует отысканию некой скалярной функции
, для которой имеют место противоречия между составляющими векторного критерия эффективности, само по себе уже представляет достаточно важную задачу, поскольку ее решение существенно уменьшает количество альтернатив. Дальнейший поиск оптимального решения заключается в выборе схемы компромисса, которая соответствует отысканию некой скалярной функции  от вектора критериев
от вектора критериев  , обеспечивающей
, обеспечивающей .
. и
и  , достигаемых при различных допустимых значениях решения
, достигаемых при различных допустимых значениях решения  очерчивает область допустимых значений критериальных функций
очерчивает область допустимых значений критериальных функций  , точки которой находятся в области компромисса (в точке
, точки которой находятся в области компромисса (в точке  имеется максимум по критерию
имеется максимум по критерию  по критерию
по критерию  , которое обеспечивает положение решения на кривой
, которое обеспечивает положение решения на кривой  удовлетворяющее некоторому принципу компромисса, определяющему правило уступки по каждому из критериев. Так, например, точка
удовлетворяющее некоторому принципу компромисса, определяющему правило уступки по каждому из критериев. Так, например, точка  и соответствующее ей решение двухкритериальной задачи выбрана в области компромисса (на кривой
и соответствующее ей решение двухкритериальной задачи выбрана в области компромисса (на кривой 
 . (12)
. (12) могут быть получены экспертным путем и задаются в абсолютном или относительном виде. В последнем случае
могут быть получены экспертным путем и задаются в абсолютном или относительном виде. В последнем случае .
. ,
, . Тогда
. Тогда ,
,  . (13)
. (13) .
.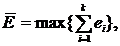

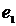 . После этого назначается некоторая уступка
. После этого назначается некоторая уступка  , которая позволяет максимизировать значение показателя
, которая позволяет максимизировать значение показателя  . Далее снова назначается уступка
. Далее снова назначается уступка  и максимизируется значение показателя
и максимизируется значение показателя  и т.д. Полученное в итоге оптимальное в рамках выбранной схемы компромисса решение обеспечивает значение показателя эффективности в пределах величин заданных уступок.
и т.д. Полученное в итоге оптимальное в рамках выбранной схемы компромисса решение обеспечивает значение показателя эффективности в пределах величин заданных уступок.