
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод динамического программированияДинамическим программированием называется метод оптимизации, в котором процесс принятия решения может быть разбит на шаги [11]. Каждый шаг переводит объект управления из состояния
Предполагается, что состояние системы
Если считать целевую функцию аддитивной от показателя эффективности каждого шага, то на шаге
Решением задачи динамического программирования является определение такого управления Для решения задачи динамического программирования был сформулирован так называемый принцип оптимальности. Его смысл которого сводится к следующему: каково бы ни было состояние Рассмотрим последний шаг 
Решение
Отыскивается условное оптимальное управление на двух последних шагах для всех возможных состояний системы на предпоследнем шаге
Состояние системы при известном управлении
В результате условной оптимизации могут быть получены последовательности значений критериальной функции и условных управлений
Решение задачи динамического программирования получается в результате подстановки конкретного значения
и так далее для всех При практической реализации метода динамического программирования на ЭВМ возникает ряд трудностей, связанных, в частности, со способами описания состояния объекта управления. Как правило, рассматривается конечное число состояний объекта управления на каждом шаге. Тем не менее, наибольший интерес представляет случай отыскания оптимального состояния объекта из бесконечного числа возможных состояний, например, методом математического программирования. В доступной литературе такие материалы отсутствуют, кроме того, не имеется сведений о программной реализации метода динамического программирования, хотя потребность в решении таких задач в достаточно велика. Из сказанного следует, что доведение методов динамического программирования до практического использования представляет собой актуальную и важную задачу исследования. Задача управления запасами Задача управления запасами впервые была описана и решена в 1915 году Фордом Хариссом. В ее основе лежит проблема, связанная с рассогласованием режимов работы поставщика и потребителя. Наличие склада позволяет обеспечить независимость работы потребителя от условий поставки материальных ресурсов. Задача управления запасами имеет цель отыскания решения, минимизирующего общие затраты на приобретение и хранение запасов. Предполагается, что общая сумма затрат на хранение запасов складывается из двух основных составляющих: затраты на пополнение запасов (издержки поставок) и затраты на собственно хранение (издержки по содержанию запаса). Издержки поставок включают стоимость получаемого товара, расходы по доставке и контролю, оформлению документации, предварительные расходы на поиск поставщика и оформление с ним договора. Часть издержек поставок зависит от размеров поставляемой партии материалов, а часть зависит только от самого факта поставки и пропорциональна числу партий. Логично предположить, что издержки поставок уменьшаются с ростом размера заказа. Тогда из соображений их уменьшения целесообразно делать заказ как можно реже максимально большим объемом. Издержки по содержанию запаса включают расходы по складскому помещению (электроэнергия, тепло), на оплату труда персонала, страховку, потери материала, на амортизацию капиталовложений в оборудование склада, потери от связывания средств в незавершенном производстве. Сюда же могут быть отнесены потери от старения товара, порчи и хищений. Естественно предположить, что издержки по содержанию запаса растут по мере увеличения объема запаса, а из соображений их уменьшения было бы хорошо иметь минимальный объем запасов и даже, если возможно, вообще отказаться от складского хозяйства. На рис. 26 представлен график зависимости величины запаса от времени. При управлении запасами необходимо выбирать момент заказа и объем партии. Сами запасы могут расходоваться также партиями, (например, суточная норма). Это обстоятельство отмечено на графике ступеньками. Отсутствие запаса на складе может привести к остановке производства и, как следствие, штрафным санкциям.
Рис. 26. Зависимость запаса от времени Пусть штрафные санкции отсутствуют. Будем считать, что издержки поставок зависят только от числа поставок, а заказ выполняется одинаковыми партиями Кроме этого будем считать, что издержки от хранения
Общие затраты на хранение имеют выраженный минимум. Поэтому возникает оптимизационная задача. Дифференцируя по
откуда размер оптимальной партии
Последнее выражение в литературе получило название формулы Уилсона или формулы наиболее экономичного объема партии. Задача управления запасами становится многономенклатурной, если в рассмотрение принимается несколько видов запасов с разными условиями поставки и расходования. В этом случае можно минимизировать как затраты на поставку и хранение каждого вида запасов, так и всех запасов совместно.
Рис. 27. Зависимость затрат на запасы |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 392. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 в состояние
в состояние  посредством управления
посредством управления  . Если общее количество шагов равно
. Если общее количество шагов равно  , то можно говорить о последовательности состояний
, то можно говорить о последовательности состояний 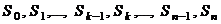 системы, которую она принимает в результате воздействия
системы, которую она принимает в результате воздействия  различных управлений
различных управлений  Целевая функция системы зависит от начального состояния и управления
Целевая функция системы зависит от начального состояния и управления .
. -того шага зависит только от предшествующего состояния
-того шага зависит только от предшествующего состояния 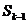 и управления на
и управления на 
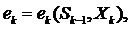 и целевая функция имеет вид
и целевая функция имеет вид
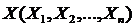 , которое переводит систему из состояния
, которое переводит систему из состояния  в состояние
в состояние  при наибольшем (наименьшем) значении
при наибольшем (наименьшем) значении  .
. системы в результате выполнения какого-либо числа шагов, управление на ближайшем шаге нужно выбирать так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к максимальному выигрышу на всех оставшихся шагах включая данный.
системы в результате выполнения какого-либо числа шагов, управление на ближайшем шаге нужно выбирать так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к максимальному выигрышу на всех оставшихся шагах включая данный. ,
,  управление, а
управление, а  - целевая функция. Согласно принципу оптимальности управление
- целевая функция. Согласно принципу оптимальности управление 

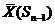 , при котором достигается
, при котором достигается 

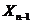 определяется как
определяется как 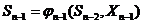 , в связи с чем целевая функция
, в связи с чем целевая функция  зависит только от состояния на предыдущем шаге и текущего управления. Далее рассматривается три, четыре и т.д. последних шага. В общем случае для шага
зависит только от состояния на предыдущем шаге и текущего управления. Далее рассматривается три, четыре и т.д. последних шага. В общем случае для шага 

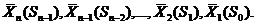
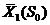 и
и  . Далее определяется состояние первого шага
. Далее определяется состояние первого шага
 и
и  и новых состояний
и новых состояний  .
.
 , следующими с интервалом
, следующими с интервалом 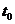 с издержками на поставку каждой партии
с издержками на поставку каждой партии  . Тогда за время
. Тогда за время  будет поставлено
будет поставлено  партий товара размером
партий товара размером  , а общие издержки составят
, а общие издержки составят  .
. пропорциональны размеру хранимой партии
пропорциональны размеру хранимой партии 
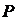 , имеем
, имеем

