
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Игры с природой с экспериментами.Рассмотренные выше игры с природой предусматривали необходимость принятия нами решения в условиях неопределенности на основе имеющихся у нас данных, используемых в процессе вычислений. Такие данные принято называть априорными. В некоторых случаях при решении задач с природными неопределенностями появляется возможность проведения различных экспериментов, позволяющих получить дополнительную информацию и тем самым снизить степень неопределенности в отношении действительного состояния природы. Очевидно, что проведение экспериментов связано с затратой ресурсов. Возникают естественные вопросы: стоит ли проводить эксперимент, сколько должно быть экспериментов, в каком порядке надо проводить эксперименты. Некоторые ответы на эти вопросы дает теория игр с экспериментами. Назовем единичным такой эксперимент, объем и порядок которого заранее определены и не могут быть изменены в процессе его проведения. Отметим, что собственно методику эксперимента должен разрабатывать специалист в предметной области, а мы можем только делать вывод о целесообразности его проведения на основании имеющейся априорной информации. Единичный эксперимент не обязательно состоит только из одного испытания. В процессе его проведения может быть получена целая выборка значений, однако принципиальным является то обстоятельство, что объем выборки Возможен и другой способ организации эксперимента. В процессе проведения эксперимента после каждого испытания мы можем принимать решение, прекратить ли дальнейшие испытания и выбрать ли какую либо стратегию из числа возможных или продолжить испытания с целью увеличения объема информации. Такие эксперименты называют последовательными. Максимальное допустимое количество выборок в процессе проведения последовательного эксперимента тоже может быть известно заранее (в этом случае говорят об усеченном последовательном эксперименте), или быть неограниченным (неограниченный последовательный эксперимент).  Будем считать, что в нашем распоряжении имеется набор
Известна также платежная матрица Наш средний выигрыш
В качестве оптимальной стратегии может быть выбрана стратегия
Предположим теперь, что в результате проведения эксперимента удалось точно установить стратегию природы
Оценим теперь средний возможный выигрыш после проведения эксперимента
где
или
Преобразовывая неравенство, имеем
Выражение в круглых скобках есть ничто иное как риск
Тогда правая часть неравенства есть минимальный средний риск, откуда вытекает условие целесообразности проведения эксперимента: затраты на эксперимент должны быть меньше минимального среднего риска, иначе от эксперимента следует воздержаться и в качестве оптимальной следует выбрать стратегию максимизирующую средний выигрыш или минимизирующую средний риск. Рассмотрим случай, когда с помощью эксперимента не удается точно определить состояние природы, но возможно получить одно из
Будем считать, что все значения
Далее для каждой стратегии рассчитаем величину условного среднего выигрыша при условии результата эксперимента
Очевидно, что оптимальной будет стратегия
Вероятность появления условного выигрыша
Величина выигрыша с использованием эксперимента
С другой стороны наш выигрыш без проведения эксперимента определяется выражением
Отсюда вытекает условие целесообразности проведения эксперимента
Если проведение эксперимента признано целесообразным, то необходимо разработать систему так называемых решающих правил, смысл которой сводится к следующему: какую стратегию |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 377. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 конечен и известен заранее.
конечен и известен заранее. стратегий
стратегий  , которые он может использовать в ответ на одну из
, которые он может использовать в ответ на одну из  возможных стратегий природы
возможных стратегий природы  , появляющуюся с вероятностью
, появляющуюся с вероятностью  при условии
при условии .
. . Для снижения неопределенности относительно действительного состояния природы мы можем провести эксперимент, стоимость которого известна и равна
. Для снижения неопределенности относительно действительного состояния природы мы можем провести эксперимент, стоимость которого известна и равна  . Пусть в результате проведения эксперимента состояние природы станет известно точно. Необходимо сделать вывод о целесообразности проведения эксперимента.
. Пусть в результате проведения эксперимента состояние природы станет известно точно. Необходимо сделать вывод о целесообразности проведения эксперимента. при использовании стратегии
при использовании стратегии  . (9)
. (9) , максимизирующая наш средний выигрыш
, максимизирующая наш средний выигрыш .
.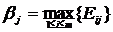 . (10)
. (10)
 ‑ стоимость проведения эксперимента. Отсюда появляется условие целесообразности проведения эксперимента
‑ стоимость проведения эксперимента. Отсюда появляется условие целесообразности проведения эксперимента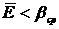
 .
. . (11)
. (11) .
. несовместимых событий
несовместимых событий 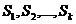 , связанных определенными вероятностями с состояниями (стратегиями) природы. Обозначим условную вероятность появления исхода
, связанных определенными вероятностями с состояниями (стратегиями) природы. Обозначим условную вероятность появления исхода  эксперимента при условии стратегии природы
эксперимента при условии стратегии природы  символом
символом 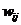 . Поскольку
. Поскольку  .
. . Определим апостериорные вероятности стратегий природы по теореме Байеса [6]
. Определим апостериорные вероятности стратегий природы по теореме Байеса [6]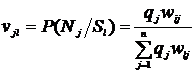 .
.
 .
. , обеспечивающая максимум условного среднего выигрыша при конкретном исходе эксперимента
, обеспечивающая максимум условного среднего выигрыша при конкретном исходе эксперимента  .
. совпадает с вероятностью появления события
совпадает с вероятностью появления события  . Обозначим ее символом
. Обозначим ее символом 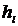 . Тогда
. Тогда .
. .
. .
.
 необходимо выбрать, если эксперимент дал результат
необходимо выбрать, если эксперимент дал результат  ?
?