
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема 22.Уравнение Шредингера
Основной характеристикой состояния квантовой системы является волновая функция Y (х, у, z, t). Вероятностьнахождения частицы в момент времени t в области с координатами х и х+dх, yиy+dy, zиz+dzопределяется: W = [Y (х, у, z, t)]2. Для определения волновой функции Y = Y (х, у, z, t) используется уравнение Шрёдингера:
где m -масса частицы, i = При движение частицы в стационарном силовом поле U(x, y, z)уравнение Шредингера имеет вид: где E -полная энергия частицы. При свободном движении частицы U(x, y, z) = 0уравнение Шредингера имеет вид:
Пример 22.1.Стационарное уравнение Шредингера имеет вид Решение: Стационарное уравнение Шредингера в общем случае имеет вид Пример 22.2.Частица находится в прямоугольном одномерном потенциальном ящике с непроницаемыми стенками шириной 0,2 нм. Если энергия частицы на втором энергетическом уровне равна 37,8 эВ, то на четвертом энергетическом уровне равна _____ эВ. Решение: Энергия частицы в прямоугольном одномерном потенциальном ящике с непроницаемыми стенками определяется из решения стационарного уравнения Шредингера:  Пример 22.3.Стационарное уравнение Шредингера имеет вид Решение: Стационарное уравнение Шредингера в общем случае имеет вид Пример 22.4.Стационарное уравнение Шредингера в общем случае имеет вид Решение: Свободной называется частица, не подверженная действию силовых полей. Это означает, что U = 0. Поэтому трехмерное движение свободной частицы описывает уравнение Пример 22.5.На рисунках схематически представлены графики распределения плотности вероятности обнаружения электрона по ширине одномерного потенциального ящика с бесконечно высокими стенками для состояний с различными значениями главного квантового числа n. В состоянии с n = 3 вероятность обнаружить электрон в интервале от l/6 до l/2 равна …
Решение: Вероятность обнаружить микрочастицу в интервале (0, l) для состояния, характеризуемого определенной Ψ-функцией, равна |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 671. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
, -мнимая единица,
-мнимая единица, 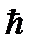 = 2π/h -постоянная Планка,
= 2π/h -постоянная Планка,  - оператор Лапласа,U(x, y, z, t) - потенциальная энергия частицы в силовом поле.
- оператор Лапласа,U(x, y, z, t) - потенциальная энергия частицы в силовом поле. ,
, .
. . Это уравнение описывает …
. Это уравнение описывает …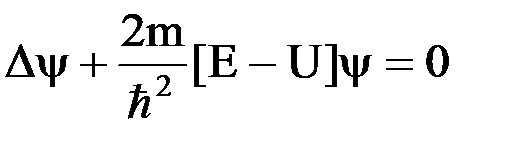 , где U = U(x,y,z) – потенциальная энергия микрочастицы. В данном случае
, где U = U(x,y,z) – потенциальная энергия микрочастицы. В данном случае 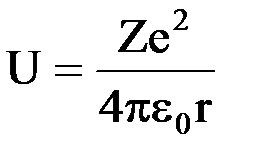 - выражение представляет собой потенциальную энергию электрона в водородоподобном атоме.
- выражение представляет собой потенциальную энергию электрона в водородоподобном атоме. . Энергия частицы может принимать следующие значения
. Энергия частицы может принимать следующие значения  , в зависимости от n – главного квантового числа, l – ширины ямы и m – массы частицы. ħ – постоянная Планка. Следовательно, энергия частицы на втором и четвертом энергетических уровнях будет определяться:
, в зависимости от n – главного квантового числа, l – ширины ямы и m – массы частицы. ħ – постоянная Планка. Следовательно, энергия частицы на втором и четвертом энергетических уровнях будет определяться:  и
и 
 . Это уравнение описывает …
. Это уравнение описывает … , где U = U(x,y,z) – потенциальная энергия микрочастицы. В данной задаче
, где U = U(x,y,z) – потенциальная энергия микрочастицы. В данной задаче  соответствует гармоническому осциллятору, то есть движению частицы под действием квазиупругой силы. Следовательно, данное уравнение описывает движение частицы под действием квазиупругой силы, то есть линейный гармонический осциллятор.
соответствует гармоническому осциллятору, то есть движению частицы под действием квазиупругой силы. Следовательно, данное уравнение описывает движение частицы под действием квазиупругой силы, то есть линейный гармонический осциллятор. . Здесь U = U(x,y,z) - потенциальная энергия микрочастицы. Трехмерное движение свободной частицы описывает уравнение …
. Здесь U = U(x,y,z) - потенциальная энергия микрочастицы. Трехмерное движение свободной частицы описывает уравнение … .
.
 . Вероятность находится как отношение площади под кривой |Ψ(x)|2 в интервале (0, b) к площади под кривой во всем интервале существования |Ψ(x)|2, то есть в интервале (l/6, l/2). Тогда в состоянии с n = 3 - вероятность обнаружить электрон в интервале от от l/6 до l/2 будет равна 1/3.
. Вероятность находится как отношение площади под кривой |Ψ(x)|2 в интервале (0, b) к площади под кривой во всем интервале существования |Ψ(x)|2, то есть в интервале (l/6, l/2). Тогда в состоянии с n = 3 - вероятность обнаружить электрон в интервале от от l/6 до l/2 будет равна 1/3.