
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема 20. Спектр атома водорода. Правило отбора
Исходя из постулатов Н. Бора: Первый постулат Бора (постулат стационарных состояний): атомная система может находится только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенная энергия En. В стационарных состояниях атом не излучает. Второй постулат Бора (правило частот): при переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний: hνnm = En – Em где h – постоянная Планка. Отсюда можно выразить частоту излучения: νnm = (En – Em)/h В видимой области излучения атома водорода наблюдаются дискретные спектральные линии (так называемый линейчатый спектр). Закономерности, которым подчиняются длины волн (или частоты) линейчатого спектра описываются формулой Ридберга:
где n и m – числа, характеризующие состояние электрона с энергией En и Em, соответственно. R = 3,29×1015 Гц – постоянная Ридберга.
Серия Бальмера - Серия Пашена - Согласно принципу Паули: 1) системы фермионов встречаются в природе только в состояниях, описываемых антисимметричными волновыми функциями; 2) В системе одинаковых фермионов любые два из них не могут находиться в одном и том же состоянии. Полное состояние электрона в атоме характеризуется квантовыми числами: главным, орбитальным, магнитным и магнитным спиновым: Главное квантовое число (n = 1, 2, 3…) определяет энергетические уровни электрона в атоме:  Момент импульса (механический орбитальный момент) электрона: Вектор момента импульса электрона (Ll )может иметь лишь такие ориентации в пространстве, при которых его проекция на направление z внешнего магнитного поля принимает квантованные значения: Собственный механический момент импульса электрона (спин) Ls:
Решение: Серию Пашена дают переходы на третий энергетический уровень m = 3, при этом энергия испускаемого кванта, следовательно, и его частота зависят от разности энергий электрона в начальном n и конечном m состояниях: Пример 20.1.На рисунке дана схема энергетических уровней атома водорода, а также условно изображены переходы электрона с одного уровня на другой, сопровождающиеся излучением кванта энергии. В ультрафиолетовой области спектра эти переходы дают серию Лаймана, в видимой области – серию Бальмера, в инфракрасной области – серию Пашена и т.д. Отношение минимальной частоты линии в серии Бальмера νmin Б к максимальной частоте линии в серии Лаймана νmin Л спектра атома водорода равно …
Решение: Энергия испускаемого кванта, следовательно, и его частота зависят от разности энергий электрона в начальном n и конечном m состояниях: Пример 20.2.Главное квантовое число n определяет … Решение: энергию стационарного состояния электрона в атоме Пример 20.3.Собственные функции электрона в атоме водорода Ψnim(r,θ,φ) содержат три целочисленных параметра: n, l и m. Параметр n называется главным квантовым числом, параметры l и m – орбитальным (азимутальным) и магнитным квантовыми числами соответственно. Орбитальное квантовое число l определяет … Решение: Момент импульса (механический орбитальный момент) электрона квантуется, принимает дискретные значения:
Решение: Магнитное квантовое число m определяет проекцию вектора |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 717. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 Серия Лаймана -
Серия Лаймана -  m = 1, n = 2, 3, 4, ... (ультрафиолетовая часть спектра)
m = 1, n = 2, 3, 4, ... (ультрафиолетовая часть спектра) m = 2, n = 3, 4, 5, ... .(видимая часть спектра)
m = 2, n = 3, 4, 5, ... .(видимая часть спектра) m = 3, n = 4, 5, 6, ... (инфракрасная часть спектра)
m = 3, n = 4, 5, 6, ... (инфракрасная часть спектра) .
. , где l = 0, 1, …, (n-1),– орбитальное квантовое число, определяет момент импульса электрона в атоме.
, где l = 0, 1, …, (n-1),– орбитальное квантовое число, определяет момент импульса электрона в атоме. , где ml = 0, ±1, ±1,…, ±l, - магнитное квантовое число, определяет проекцию момента импульса электрона на заданное направление.
, где ml = 0, ±1, ±1,…, ±l, - магнитное квантовое число, определяет проекцию момента импульса электрона на заданное направление. ,где s – спиновое квантовое число (s = 1/2).
,где s – спиновое квантовое число (s = 1/2). Пример 20.1.На рисунке схематически изображены стационарные орбиты электрона в атоме водорода согласно модели Бора, а также показаны переходы электрона с одной стационарной орбиты на другую, сопровождающиеся излучением кванта энергии. В ультрафиолетовой области спектра эти переходы дают серию Лаймана, в видимой – серию Бальмера, в инфракрасной – серию Пашена. Наибольшей частоте кванта в серии Пашена (для переходов, представленных на рисунке) соответствует переход …
Пример 20.1.На рисунке схематически изображены стационарные орбиты электрона в атоме водорода согласно модели Бора, а также показаны переходы электрона с одной стационарной орбиты на другую, сопровождающиеся излучением кванта энергии. В ультрафиолетовой области спектра эти переходы дают серию Лаймана, в видимой – серию Бальмера, в инфракрасной – серию Пашена. Наибольшей частоте кванта в серии Пашена (для переходов, представленных на рисунке) соответствует переход … . Поэтому наибольшей частоте кванта в серии Пашена (для переходов, представленных на рисунке) соответствует переход n = 5 → m = 3.
. Поэтому наибольшей частоте кванта в серии Пашена (для переходов, представленных на рисунке) соответствует переход n = 5 → m = 3.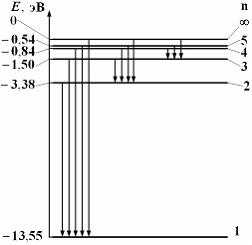
 . Серию Лаймана дают переходы на первый энергетический уровень m = 1, серию Бальмера – на второй уровень m = 2. Максимальная частота линии в серии Лаймана будет наблюдаться при переходе с максимально возможного уровня n = ∞:
. Серию Лаймана дают переходы на первый энергетический уровень m = 1, серию Бальмера – на второй уровень m = 2. Максимальная частота линии в серии Лаймана будет наблюдаться при переходе с максимально возможного уровня n = ∞: 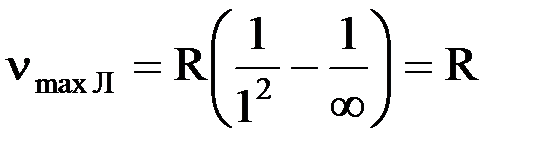 . Минимальная частота линии в серии Бальмера наблюдается при переходе электрона с третьего уровня n = 3:
. Минимальная частота линии в серии Бальмера наблюдается при переходе электрона с третьего уровня n = 3:  . Тогда
. Тогда  .
. , где Z – заряд ядра, m – масса электрона, e –заряд электрона, h – постоянная Планка, ε0 – диэлектрическая проницаемость.
, где Z – заряд ядра, m – масса электрона, e –заряд электрона, h – постоянная Планка, ε0 – диэлектрическая проницаемость.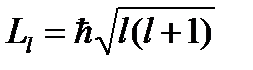 , где l = 0, 1, …, (n-1),– орбитальное квантовое число, определяет модуль момента импульса электрона в атоме.
, где l = 0, 1, …, (n-1),– орбитальное квантовое число, определяет модуль момента импульса электрона в атоме. Пример 20.4.Момент импульса электрона в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса
Пример 20.4.Момент импульса электрона в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса  электрона. На рисунке приведены возможные ориентации вектора
электрона. На рисунке приведены возможные ориентации вектора  . Минимальное значение главного квантового числа n для указанного состояния равно …
. Минимальное значение главного квантового числа n для указанного состояния равно …