Тема 5. Распределение Максвелла и Больцмана

В случае анализа свойств макроскопических систем (МС), например, идеального газа, бесполезно интересоваться физическими свойствами отдельных частиц в данный момент времени, но важно знать, какова вероятность присутствия в системе частиц с тем или иным значением физической величины. Законы распределения – это закономерности устанавливающие связь между физическими величинами в МС с вероятностью их присутствия в системе при определенных условиях.

Если система состоит из идентичных, различных частиц, которые могут обладать любым значением спина, то ее физическая статистика определяется распределением Больцмана:

,

- вероятность того, что частицы системы обладают энергией E_i при температуре Т; В – коэффициент, определяемый физической величиной r. Например, идеальный газ подчиняется распределению Больцмана.

Из распределения Больцмана следует распределение Максвелла – распределение молекул идеального газа по скоростям:

,

где m₀ – масса молекулы. Кривая распределения имеет максимум соответствующий наиболее вероятной скорости молекул газа при данной температуре:

.

На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла). Свойства распределения Максвелла:

1)   - доля молекул, скорости которых заключены в интервале скоростей отuдоu+Du в расчете на единицу этого интервала;

2) площадь под кривой всегда равна единице;

3) если не меняя температуры взять другой газ с меньшей молярной массой и таким же числом молекул, то площадь под кривой не изменятся, величина максимума уменьшится, максимум сместится вправо в сторону больших скоростей;

4) если не меняя температуры взять другой газ с большей молярной массой и таким же числом молекул, то площадь под кривой не изменятся, величина максимума увеличится, максимум сместится влево в сторону меньших скоростей;

5) если увеличить температуру- максимум сместится вправо в сторону больших скоростей, величина максимума уменьшится;

6) если уменьшить температуру- максимум сместится влево в сторону меньших скоростей, величина максимума увеличится.

Пример 5.1. На рисунке (см. выше приведенный рисунок) представлен график распределения молекул идеального газа по скоростям (распределение Максвелла), где f(v) – доля молекул, скорости которых заключены в интервал отv до v+dv в расчете на единицу этого интервала. Если, не меняя температуры и числа молекул, взять другой газ с меньшей молярной массой, то

Rмаксимум сместится вправо в сторону больших скоростей

£максимум сместится влево в сторону меньших скоростей

£площадь под кривой уменьшится

Решение: смотри 2 и 4 свойство функции распределения.

Пример 5.2.В трех одинаковых сосудах при равных условиях находится одинаковое количество водорода (μ=0,002 кг/моль), гелия (μ=0,004 кг/моль), азота(μ=0,014 кг/моль). Какая кривая соответствует распределению молекул водорода?

Решение: кривая распределения имеет максимум при скоростипрямо пропорциональный температуре и обратно пропорциональный массе молекул: . Масса молекул водорода минимальна из всех приведенных, значит, ей соответствует кривая (3) с наибольшим значением v_m.

Распределение скоростей молекул гелия будет описывать кривая 2, азота – 1.

Пример 5.3. Используем тот же рисунок, газ находится при разных температурах, какая кривая соответствует минимальной температуре?

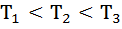Решение: кривая распределения имеет максимум при скоростипрямо пропорциональный температуре, следовательно минимальная температура – минимальная скорость, это кривая (1). Соотношение между температурами: . Кроме того, на рисунке верно изображено увеличение величины максимума при его смещении в сторону меньших скоростей при понижении температуры.