
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема 3. Динамика вращательного движения
Динамика вращения 1) Тогда момент силы - произведение силы на плечо 2) момент импульса – произведение момента инерции на угловую скорость вращения 3) момент инерции – определяется распределением массы тела относительно оси вращения: a) материальной точки b)момент инерции тонкостенного цилиндра или кольца относительно геометрической оси c) момент инерции сплошного однородного цилиндра или дискаотносительно геометрической оси d) момент инерции однородного шара относительно оси проходящей через его центр e) теорема Штейнера – момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно параллельной оси проходящей через центр масс тела и произведения массы тела на квадрат расстоянияот центра масс до оси вращения: 4) Основное уравнение динамики вращательного движения: Первая формулировка -момент вращающей силы относительно оси вращения равен произведению углового ускорения и момента инерции тела относительно этой оси:  Вторая формулировка – момент вращающей силы равен первой производной момента импульса тела по времени: Пример 3.1. Момент импульса тела относительно неподвижной оси изменяется по закону Решение: Согласно основному уравнению динамики вращения
Решение: момент импульса L=Iw=constлиния (Е). Пример 3.3. Момент импульса вращающегося тела изменяется по закону L=at, где a - некоторая положительная константа. Момент инерции тела постоянный. При этом угловое ускорение тела зависит от времени согласно графику… Решение: угловое ускорение найдем из основного уравнения вращения Момент силы -
Пример 3.4.Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за его середину. Если он повернет шест из горизонтального положения в вертикальное, то частота вращения в конечном состоянии: £ не изменится £уменьшится R увеличится Решение: по закону сохранения момента импульса L=wI=const, изменение частоты вращения (w) произойдет при изменении момента инерции человека с шестом (I). Если шест развернуть из горизонтального положения ввертикальное (т.е. расположить его вдоль оси вращения), его момент инерции обратиться в ноль, момент инерции человека с шестом уменьшится, при этом частота вращения должна увеличится для сохранения момента импульса. Пример 3.5.При расчете моментов инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера. Если ось вращения тонкого кольца перенести из центра масс на край, то момент инерции относительно новой оси увеличится в … раза.
Решение:момент инерции тонкостенного цилиндра или кольца относительно геометрической оси, равен: £I1<I2<I3 £I1>I2>I3 RI1= I2<I3 £I1<I2= I3
R увеличится £уменьшится £ не изменится Решение:момент инерции материальной точки - Моментыинерции: I1= 1×32=9, I2= 2, I3= 3, I4= 36. Момент инерции системы: I = 9+2+3+36=50 г×см2. Если поменять местами 1 и 3 шарики, то I= 27+2+1+36 = 66 г×см2. Момент инерции системы увеличился. Можно было ответить на вопрос задачи без расчета: третий – тяжелый шарик переносится дальше от оси вращения, значит, момент инерции увеличится. Пример 3.8. К точке, лежащей на внешней поверхности диска, приложены 4 силы (рис. а). Если ось вращения проходит через центр О диска перпендикулярно плоскости рисунка, то плечо силы F1 равно… Rb £ ноль £c £a
Пример 3.9. Физический маятник совершает колебания вокруг оси, проходящей через т. О перпендикулярно плоскости рисунка. Для
£ вверх в плоскости рисунка £ к нам перпендикулярно плоскости рисунка £ вниз в плоскости рисунка Решение: под действие силы тяжести маятник движется влево. Расположим большой палец правой руки вдоль оси вращения так чтобы четыре пальца двигались в направлении движения маятника, получим направление большого пальца от нас перпендикулярно плоскости рисунка – это и есть направление момента силы тяжести.
£ М1= М2 = М3, М4 = 0 RМ1> М2 > М3, М4 = 0 £ М1< М2 < М3< М4 £М2> М1> М3, М4 = 0 Решение: момент силы - Пример 3.11. Диск радиусом 1 м, способный свободно вращаться вокруг горизонтальной оси, проходящей через точку О перпендикулярно плоскости рисунка, отклонили от вертикали на угол 900 и отпустили. В начальный момент времени угловое ускорение диска равно (с-2): R7 £10 £5 £20
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1611. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 момент силы–векторное произведение радиус-вектора, проведенного от оси к точке приложения силы и силы
момент силы–векторное произведение радиус-вектора, проведенного от оси к точке приложения силы и силы  , модуль момента силы равен
, модуль момента силы равен  , где a - угол между направлением rиF.
, где a - угол между направлением rиF.  – плечо силы– расстояние от оси до направления действия силы (из оси опускается перпендикуляр на направление действия силы).
– плечо силы– расстояние от оси до направления действия силы (из оси опускается перпендикуляр на направление действия силы). . М – это псевдовектор, направлен вдоль оси вращения в соответствии с правилом правой руки –четыре пальца вращаются в направлении действия силы – большой укажет направление момента силы.
. М – это псевдовектор, направлен вдоль оси вращения в соответствии с правилом правой руки –четыре пальца вращаются в направлении действия силы – большой укажет направление момента силы. , псевдовектор направлен вдоль оси вращения (правая рука вращается по направлению вращения тел.
, псевдовектор направлен вдоль оси вращения (правая рука вращается по направлению вращения тел.

 m
m  .
. .
. .
. .
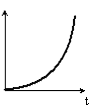
. . Укажите график, зависимости от времени момента сил, действующих на тело.
. Укажите график, зависимости от времени момента сил, действующих на тело. .
.


 ) :
) :  .
.

 £ 4 £ 1,5 R 2 £ 3
£ 4 £ 1,5 R 2 £ 3 . Для расчета момента инерции относительно параллельной оси применим теорему Штейнера
. Для расчета момента инерции относительно параллельной оси применим теорему Штейнера  . Ответ:
. Ответ:  . Пример 3.6. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали пополам вдоль разных осей симметрии. Затем все части отодвинули друг от друга на разное расстояние и расставили симметрично относительно оси ОО’. Для моментов инерции относительно этой оси справедливо соотношение…
. Пример 3.6. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали пополам вдоль разных осей симметрии. Затем все части отодвинули друг от друга на разное расстояние и расставили симметрично относительно оси ОО’. Для моментов инерции относительно этой оси справедливо соотношение… Решение:момент инерции тела определяется распределением массы этого тела относительно оси вращения. На первом и втором рисунке части эллипса расположены одинаково относительно оси ОО’, значит, их моменты инерции одинаковы. На третьем рисунке части эллипса дальше от оси вращения – момент инерции больше.
Решение:момент инерции тела определяется распределением массы этого тела относительно оси вращения. На первом и втором рисунке части эллипса расположены одинаково относительно оси ОО’, значит, их моменты инерции одинаковы. На третьем рисунке части эллипса дальше от оси вращения – момент инерции больше. Пример 3.7.Четыре шарика расположены вдоль прямойа. Расстояния между соседними шариками одинаковы. Массы шариков слева направо, в граммах: 1, 2 , 3 , 4.Если поменять местами шарики 1 и 3, то момент инерции этой системы относительно осиО, перпендикулярной прямой а и проходящей через середину системы ...
Пример 3.7.Четыре шарика расположены вдоль прямойа. Расстояния между соседними шариками одинаковы. Массы шариков слева направо, в граммах: 1, 2 , 3 , 4.Если поменять местами шарики 1 и 3, то момент инерции этой системы относительно осиО, перпендикулярной прямой а и проходящей через середину системы ... , системы точек – сумма моментов инерции точек. Пусть расстояние между шариками 2cм, тогда: r1=3cм, r2=1cм, r3=1cм, r4=3 cм.
, системы точек – сумма моментов инерции точек. Пусть расстояние между шариками 2cм, тогда: r1=3cм, r2=1cм, r3=1cм, r4=3 cм. Решение: плечо силы – это расстояние от оси до направления действия силы, т.е. плечо совпадает с перпендикуляром проведенным от оси до направление действия силы. Продлим направление действия силы F1 (см. рис. б). Опустим на это направление из точки О перпендикуляр – получим отрезок (ОА) – это и есть плечо силы F1, оно совпадает с отрезком (b).Для других сил l2 = 0; l3 = a; l4 = c.
Решение: плечо силы – это расстояние от оси до направления действия силы, т.е. плечо совпадает с перпендикуляром проведенным от оси до направление действия силы. Продлим направление действия силы F1 (см. рис. б). Опустим на это направление из точки О перпендикуляр – получим отрезок (ОА) – это и есть плечо силы F1, оно совпадает с отрезком (b).Для других сил l2 = 0; l3 = a; l4 = c.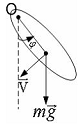 R от нас перпендикулярно плоскости рисунка
R от нас перпендикулярно плоскости рисунка Пример 3.10. Диск может вращаться вокруг оси перпендикулярной плоскости диска и проходящей через его центр. В точке А прикладывают одну из сил, лежащих в плоскости диска. Верным для моментов этих сил относительно рассматриваемой оси является соотношение …
Пример 3.10. Диск может вращаться вокруг оси перпендикулярной плоскости диска и проходящей через его центр. В точке А прикладывают одну из сил, лежащих в плоскости диска. Верным для моментов этих сил относительно рассматриваемой оси является соотношение … . Угол междуF4и ra4=0, sina4=0 - М4 = 0. Для других сил
. Угол междуF4и ra4=0, sina4=0 - М4 = 0. Для других сил 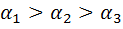 , значит
, значит  .
. Решение: согласно основному закону динамики вращения твердого тела
Решение: согласно основному закону динамики вращения твердого тела  , где R – радиус диска и плечо силы. Момент инерции диска определим по теореме Штейнера:
, где R – радиус диска и плечо силы. Момент инерции диска определим по теореме Штейнера: , тогда
, тогда .
.