
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лекция 24. Криволинейные интегралы ⇐ ПредыдущаяСтр 7 из 7
План лекции 1. Задачи, приводящие к криволинейному интегралу первого рода 2. Криволинейный интеграл первого рода и его вычисление 3. Задачи, приводящие к криволинейному интегралу второго рода 4. Криволинейный интеграл второго рода и его вычисление 5. Свойства криволинейного интеграла Введение Часто в практических задачах может возникать необходимость определить длину траектории движения тела или определить среднее значение массы или температуры длинного, тонкого, а зачастую и криволинейного объекта; или, например, определить количество вещества в кривой трубке и т. д. Очевидно, что подобные задачи должны также решаться интегральными методами. В лекции рассматриваются подходы к их решению. Для лучшего понимания криволинейных интегралов рекомендуется повторить определенный интеграл и кратные интегралы. Понятие криволинейного интеграла необходимо при изучении поверхностного интеграла, элементов теории поля, а также при решении прикладных задач, связанных с определением масс, объемов, средних значений тонких объектов, например, вдоль оптического луча, и др. 1. Задачи, приводящие к криволинейному интегралу первого рода

2. Криволинейный интеграл первого рода и его вычисление
Пусть функция
где L – область интегрирования, Определение 1. Кривая называется простой, если она не содержит самопересечений. Определение 2. Кривая называется гладкой, если она не содержит особых точек, где не существует ее производной. Определение 3. Кривая называется спрямляемой, если она имеет конечную длину. Теорема 1 (о существовании криволинейного интеграла). Если функция 2.2. Вычисление криволинейного интеграла Вычисление криволинейного интеграла сводится к вычислению определенного интеграла. Если кривая L задана параметрически
 . (3) . (3)
Если кривая L задана явно в декартовой системе координат
Внимание! Сравните (3) и (4) с выражениями для длины дуги (л. 17). 3. Задачи, приводящие к криволинейному интегралу второго рода
4. Криволинейный интеграл второго рода и его вычисление 4.1. Определение криволинейного интеграла
 определена на плоской кривой L.. Разобьем область определения L на n частей, длины которых обозначим определена на плоской кривой L.. Разобьем область определения L на n частей, длины которых обозначим 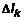 . В k-той части выберем точку . В k-той части выберем точку  , вычислим в ней значение функции и скалярное произведение , вычислим в ней значение функции и скалярное произведение  . Интегральная сумма функции по кривой . Интегральная сумма функции по кривой  . Найдем предел интегральной суммы при . Найдем предел интегральной суммы при  . Если этот предел существует и не зависит ни от способа разбиения кривой L на части, ни от выбора точки в каждой части, то он называется криволинейным интегралом второго рода, или криволинейным интегралом по координатам и обозначается . Если этот предел существует и не зависит ни от способа разбиения кривой L на части, ни от выбора точки в каждой части, то он называется криволинейным интегралом второго рода, или криволинейным интегралом по координатам и обозначается
где Замечание! Теорема существования та же, что и для интеграла первого рода. 4.2. Вычисление криволинейного интеграла Вычисление криволинейного интеграла сводится к вычислению определенного интеграла. Если кривая L задана параметрически
Аналогично определим правило вычисления второй составляющей
4.3. Правило вычисления
 и определить дифференциалы и определить дифференциалы  через параметр t, исходя из уравнения кривой L, а за пределы интегрирования принять значения этой переменной в начале и в конце дуги. через параметр t, исходя из уравнения кривой L, а за пределы интегрирования принять значения этой переменной в начале и в конце дуги.
Частный случай! Очевидно, что если кривая L задана явно,
5. Свойства криволинейного интеграла Поскольку принципиальных различий в определении интегралов нет, то все свойства определенного интеграла справедливы и для криволинейных интегралов, однако криволинейный интеграл второго рода имеет свои особые свойства. 1. При изменении направления обхода кривой знак криволинейного интеграла второго рода меняется на противоположный
Интеграл по замкнутому контуру обозначается 2. Криволинейный интеграл второго рода по замкнутому контуру не зависит от выбора начальной точки на контуре.
 3. Если область, ограниченная замкнутым контуром разбита на две части, то интеграл по этому контуру равен сумме двух интегралов по замкнутым контурам, ограничивающим части области в том же направлении (рис. 3) 3. Если область, ограниченная замкнутым контуром разбита на две части, то интеграл по этому контуру равен сумме двух интегралов по замкнутым контурам, ограничивающим части области в том же направлении (рис. 3)  . .
ПРИМЕР 1. Найти Заключение Предложенный материал лекции повышенной сложности. Поэтому для лучшего усвоения рекомендуется прочесть его еще раз и обратить внимание на важные замечания. Напомним, что все основные результаты, представленные в лекции, также строятся на одном принципе разбиение и предельный переход, что облегчает ее понимание. Рассмотренные выражения необходимы при решении таких прикладных задач, где необходимо определять интеграл вдоль некоторой кривой. Приложения криволинейного интеграла будут рассматриваться в следующей лекции. Отметим, что: - криволинейный интеграл эквивалентен замене переменной в определенном интеграле согласно уравнению кривой, при этом пространство как бы «искривлено»; - криволинейный интеграл первого рода – это интеграл функции по длине дуги; - криволинейный интеграл второго рода – это интеграл векторной функции по кривой; - вычисление криволинейных интегралов сводится к нахождению определенного интеграла; - в криволинейном интеграле общие пределы интегрирования; - все выводы для плоской кривой справедливы и для пространственных кривых с обобщением путем добавления третьей переменной. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Ростов-на-Дону: Феникс, 1997.– 512 с.
Цель лекции: Научиться использовать известные методы интегрирования при взятии криволинейных интегралов, уметь применять полученные знания в прикладных задачах. План лекции 1. Формула Грина 2. Условия независимости от пути интегрирования 3. Приложения криволинейных интегралов Введение В предыдущей лекции рассматривался один из разделов интегрального исчисления «Криволинейный интеграл» и обозначен круг задач, при решении которых необходимо использовать такое интегрирование. В лекции раскрываются прикладные возможности использования таких интегралов. Для раскрытия всех возможностей даются теоремы, позволяющие решать специализированные задачи. 1. Формула Грина Теорема 1 (формула Грина). Если функции
Для сложной петли (рис. 2) справедливо
Найти 2. Условия независимости от пути интегрирования
Для того чтобы Доказательство (необходимость). Дано Доказательство (достаточность). Дано
Для того чтобы криволинейный интеграл
Доказательство от противного (необходимость). Дано
Дано Следствие! Если
ПРИМЕР 2.
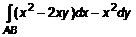 для для  и и  . Обозначим . Обозначим  и и  . Тогда . Тогда  и и  , т. е. , т. е.  и интеграл не зависит от пути интегрирования. Запишем уравнение прямой и интеграл не зависит от пути интегрирования. Запишем уравнение прямой  : :  , или , или  . По правилу интегрирования подставим в подынтегральное выражение . По правилу интегрирования подставим в подынтегральное выражение  . Окончательный ответ предлагается получить самостоятельно. Сравните результат, если в качестве пути интегрирования взять . Окончательный ответ предлагается получить самостоятельно. Сравните результат, если в качестве пути интегрирования взять  . .
3. Приложения криволинейных интегралов 3.1. Работа силы Пусть
Касательный вектор Замечания! 1. 2. Криволинейный интеграл второго рода связан с интегралом первого рода: 3.2. Вычисление площади плоской фигуры По формуле Грина
2.
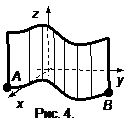 3. 3.  , ,  , тогда , тогда 
3.3. Вычисление массы кривой Если задана кривая
3.4. Площадь цилиндрической поверхности Если направляющей цилиндрической поверхности служит кривая ПРИМЕР 3. Определить массу кривой
ПРИМЕР 4. Вычислить площадь фигуры
Несмотря на то, что сегодняшняя лекция посвящена практическому приложению криволинейного интеграла, отметим, что подробное рассмотрение классических прикладных задач позволит в будущем правильно ставить подобные задачи и правильно их решать. Для лучшего усвоения материала предлагается сравнить подходы, используемые в лекции «Приложения определенного интеграла», с подходами, использованными в данной лекции. Основное внимание необходимо обратить на формулу Грина которая используется в векторном анализе. Материал лекции необходим, прежде всего, для решения прикладных задач. Кроме того, понимание общности в решении интегральных задач необходимо при изучении поверхностного интеграла. Отметим, что: - если - двойной интеграл связан с криволинейным интегралом; - криволинейный интеграл второго рода связан с криволинейным интегралом первого рода; - криволинейный интеграл по замкнутому контуру равен площади фигуры, ограниченной этим контуром; - если Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Ростов-на-Дону: Феникс, 1997.– 512 с. 3. Фихтенгольц Г.М. Основы математического анализа. Часть 2 – М.: Лань, 2002. - 464 с.
Цель занятия: изучить понятие поверхностного интеграла; научиться определять тип задач, приводящих к поверхностному интегралу, вычислять поверхностный интеграл. План лекции 1. Задачи, приводящие к поверхностному интегралу первого рода 2. Поверхностный интеграл первого рода и его вычисление 3. Задачи, приводящие к поверхностному интегралу второго рода 4. Поверхностный интеграл второго рода и его вычисление 5. Связь поверхностного интеграла с криволинейными и кратными интегралами Введение В практических задачах может возникать необходимость определить плотность поверхностного заряда криволинейной поверхности или плотность потока тепла через нее. Кроме того, есть задачи, посвященные определению среднего значения массы или температуры тонкой криволинейной поверхности, и т. д. Очевидно, что подобные задачи должны также решаться интегральными методами. В лекции рассматриваются подходы к их решению. Особое внимание следует обратить на общность всех изученных ранее типов интегралов, показана их взаимосвязь, что позволяет легче понять геометрический и физический смысл этих интегралов. 1. Задачи, приводящие к поверхностному интегралу первого рода
2. Поверхностный интеграл первого рода и его вычисление 2.1. Определение поверхностного интеграла
 определена на поверхности определена на поверхности  . Разобьем поверхность . Разобьем поверхность  на n частей произвольными линиями, площади которых обозначим на n частей произвольными линиями, площади которых обозначим 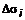 . В i-той части выберем произвольную точку . В i-той части выберем произвольную точку  , вычислим в ней значение функции и произведения , вычислим в ней значение функции и произведения  . Составим интегральную сумму всех произведений . Составим интегральную сумму всех произведений  . Найдем предел интегральной суммы при . Найдем предел интегральной суммы при  . Если этот предел существует и не зависит ни от способа разбиения поверхности . Если этот предел существует и не зависит ни от способа разбиения поверхности  на части, ни от выбора точки в каждой части, то он называется поверхностным интегралом первого рода и обозначается на части, ни от выбора точки в каждой части, то он называется поверхностным интегралом первого рода и обозначается
где Определение 1. Теорема 1 (о существовании поверхностного интеграла). Если функция Выводы! 1. Свойства поверхностного интеграла первого рода те же, что и двойного. 2. Двойной интеграл есть частный случай поверхностного интеграла, поэтому при вычислении он сводится к своему частному случаю. 2.2. Вычисление поверхностного интеграла Пусть задана поверхность
Если использовать (3) в выражении (2), тогда вычисление криволинейного интеграла по поверхности
2.3. Приложения поверхностного интеграла 1. Величина заряда на поверхности 2. Масса поверхности 3. Статистические моменты 4. Моменты инерции 3. Задачи, приводящие к поверхностному интегралу второго рода
Определение 1. Потоком жидкости через поверхность называется количество жидкости m, протекающей через эту поверхность за единицу времени.
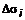 , где , где  . На i-том произвольном участке выберем точку . На i-том произвольном участке выберем точку  и вычислим в ней значение скорости и вычислим в ней значение скорости 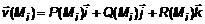 . Обозначим вектор нормали к этой части в точке . Обозначим вектор нормали к этой части в точке  через через  (рис. 3). Если принять участки поверхности плоскими, то за единицу времени (рис. 3). Если принять участки поверхности плоскими, то за единицу времени  через данный участок в направлении через данный участок в направлении  вытек объем жидкости вытек объем жидкости  , равный объему наклонной призмы с высотой , равный объему наклонной призмы с высотой  . Пусть скорость в пределах i-той части не меняется. Тогда поток жидкости через элементарный участок . Пусть скорость в пределах i-той части не меняется. Тогда поток жидкости через элементарный участок 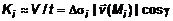 . Помножим это уравнение на . Помножим это уравнение на 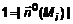 , ,   , где , где 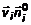 – скалярное произведение. Поток – скалярное произведение. Поток  через всю поверхность через всю поверхность  определяется суммой потоков через элементарные поверхности. определяется суммой потоков через элементарные поверхности.  . Обозначим . Обозначим  , тогда , тогда
 . (5) . (5)
4. Поверхностный интеграл второго рода и его вычисление 4.1. Двусторонние поверхности и их ориентация
Поверхность называется двусторонней, если, выходя из любой ее точки, можно прийти в ту же точку с противоположным направлением нормали только, пересекая границу поверхности. Если это условие не выполняется, то поверхность называется односторонней, например, петля Мебиуса. Замечание! Все изученные ранее поверхности двусторонние.
4.2. Определение поверхностного интеграла Пусть на поверхности
 . (6) . (6)
Аналогичные интегралы можно получить для других проекций
тогда поверхностный интеграл второго рода общего вида запишем как
Свойство! Поверхностный интеграл второго рода изменяет свой знак при изменении ориентации поверхности. 4.3. Вычисление поверхностного интеграла Если Аналогичные интегралы можно получить для других проекций
где знак «+» соответствует острому углу между нормалью и проекционной осью, а знак «–» тупому углу. 5. Связь поверхностного интеграла с криволинейными и кратными интегралами
Если функции
Вывод! Формула Грина – это частный случай теоремы Стокса Теорема 2 (Остроградского–Гаусса). Если функции
Заключение Материал лекции является промежуточным звеном между темами «Интегральное исчисление» и «Теория поля, векторный анализ». Он позволяет найти общность в построении задач и подходов, используемых в этих двух темах. Все типы интегралов связаны между собой и вычисление любого из них сводится к вычислению определенного интеграла. Поверхностные используются при вычислении расходов биоресурсов, давления на поверхность, процессов теплообмена и др. Отметим, что: - поверхностные интегралы – это интегралы по поверхности; - поверхностный интеграл первого рода – это двойной интеграл от явной функции по проекции поверхности; - поверхностный интеграл второго рода – это двойной интеграл от векторной функции по проекциям поверхности на соответствующие координатные плоскости; - формула Грина частный случай теоремы Стокса; - формулы Стокса и Остроградского–Гаусса связывают поверхностный интеграл 2-го рода с двойными и тройным интегралами. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с.
|
 Пусть вдоль плоской кривой L (рис. 1) неравномерно распределена масса с линейной плотностью
Пусть вдоль плоской кривой L (рис. 1) неравномерно распределена масса с линейной плотностью  . Необходимо определить массу кривой. Если
. Необходимо определить массу кривой. Если  , то
, то  , где
, где  – длина дуги
– длина дуги  , где
, где  . Возьмем i-тую часть (
. Возьмем i-тую часть (  ), в которой произвольно выберем точку
), в которой произвольно выберем точку  и вычислим в ней значение плотности
и вычислим в ней значение плотности 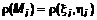 . Предположим, что в пределах выбранной части плотность постоянна и равна
. Предположим, что в пределах выбранной части плотность постоянна и равна  , тогда масса i-той части
, тогда масса i-той части  . Аналогично определим массы всех частей. Тогда масса всей кривой приближенно определяется интегральной суммой
. Аналогично определим массы всех частей. Тогда масса всей кривой приближенно определяется интегральной суммой  . Обозначим
. Обозначим  , тогда точное значение массы
, тогда точное значение массы . (1)
. (1) определена на плоской кривой L.. Разобьем область определения L на n частей, длины которых обозначим
определена на плоской кривой L.. Разобьем область определения L на n частей, длины которых обозначим  . В i-той части выберем произвольную точку
. В i-той части выберем произвольную точку  , вычислим в ней значение функции и произведения
, вычислим в ней значение функции и произведения 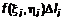 . Составим интегральную сумму всех произведений
. Составим интегральную сумму всех произведений  . Найдем предел суммы при
. Найдем предел суммы при  . Если этот предел существует и не зависит ни от способа разбиения кривой L на части, ни от выбора точки в каждой части, то он называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги, и обозначается
. Если этот предел существует и не зависит ни от способа разбиения кривой L на части, ни от выбора точки в каждой части, то он называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги, и обозначается , (2)
, (2) – дифференциал длины дуги.
– дифференциал длины дуги.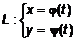 , где
, где  ,
,  и
и  – непрерывно дифференцируемы и
– непрерывно дифференцируемы и  , то
, то , где
, где  и
и  – непрерывно дифференцируема, то
– непрерывно дифференцируема, то . (4)
. (4) Вдоль плоской кривой под действием силы
Вдоль плоской кривой под действием силы  на прямолинейном участке
на прямолинейном участке  , то работа определяется как
, то работа определяется как  . Разобьем кривую на n частей длиной
. Разобьем кривую на n частей длиной  . На k-той дуге (
. На k-той дуге (  ) произвольно выберем точку
) произвольно выберем точку 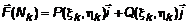 . Пусть сила в пределах этой дуги не менялась, а перемещение осуществлялось по вектору
. Пусть сила в пределах этой дуги не менялась, а перемещение осуществлялось по вектору 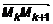 . Тогда приближенно работа на этой дуге равна
. Тогда приближенно работа на этой дуге равна  ,
,  или
или 
 . Составим интегральную сумму
. Составим интегральную сумму  . Обозначим
. Обозначим  , и
, и . (5)
. (5) , (6)
, (6) – криволинейный интеграл второго рода общего вида.
– криволинейный интеграл второго рода общего вида. получена разбиением кривой L на n частей точками
получена разбиением кривой L на n частей точками 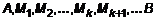 , которым соответствует значение параметра
, которым соответствует значение параметра  . Тогда
. Тогда  , откуда по теореме Лагранжа
, откуда по теореме Лагранжа  , где
, где  и
и  . Точку
. Точку  , тогда
, тогда  , тогда
, тогда . (7)
. (7) . (8)
. (8) , причем a – абсцисса точки A и b – абсцисса точки B, то вычисление сводится к интегралу
, причем a – абсцисса точки A и b – абсцисса точки B, то вычисление сводится к интегралу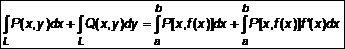 . (9)
. (9) .
. . Направление обхода контура считается положительным, если фигура, им ограниченная, остается слева
. Направление обхода контура считается положительным, если фигура, им ограниченная, остается слева  , и отрицательным, если остается справа
, и отрицательным, если остается справа  , и обозначается
, и обозначается  и
и  .
. по
по  от точки
от точки  до
до  .
. и
и  непрерывно дифференцируемы в любой точке области определения D, ограниченной, замкнутой, гладкой кривой L (рис. 1), то
непрерывно дифференцируемы в любой точке области определения D, ограниченной, замкнутой, гладкой кривой L (рис. 1), то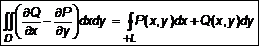 . (1)
. (1) Доказательство.
Доказательство. .
.

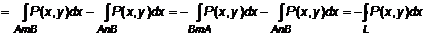 Аналогично можно показать, что
Аналогично можно показать, что  . Тогда вычитая из последнего выражения первое, получим выражение (1).
. Тогда вычитая из последнего выражения первое, получим выражение (1).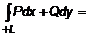





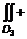
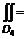

 ПРИМЕР 1.
ПРИМЕР 1. , если
, если  .
.  ,
,  . Согласно (1)
. Согласно (1)  . В полярных координатах
. В полярных координатах 
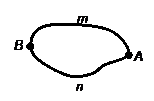 Теорема 2 (лемма).
Теорема 2 (лемма). не зависел от пути интегрирования необходимо и достаточно, чтобы
не зависел от пути интегрирования необходимо и достаточно, чтобы 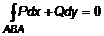 .
. , т. е.
, т. е.  . Согласно свойствам интеграла
. Согласно свойствам интеграла  .
. , тогда
, тогда  или
или  , откуда
, откуда 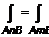 .
. .
. не зависит от пути интегрирования. Требуется доказать, что
не зависит от пути интегрирования. Требуется доказать, что  в некоторой точке
в некоторой точке  . Обозначим окрестность этой точки
. Обозначим окрестность этой точки  , ограниченной кривой
, ограниченной кривой  (рис. 3). Согласно формуле Грина
(рис. 3). Согласно формуле Грина 
 , следовательно,
, следовательно,  и
и  , что не верно.
, что не верно. Доказательство (достаточность).
Доказательство (достаточность). . Тогда, на основании теоремы 2 криволинейный интеграл не зависит от пути интегрирования.
. Тогда, на основании теоремы 2 криволинейный интеграл не зависит от пути интегрирования. есть дифференциал некоторой функции, и обобщенная формула Ньютона–Лейбница будет иметь вид
есть дифференциал некоторой функции, и обобщенная формула Ньютона–Лейбница будет иметь вид . (2)
. (2) . (3)
. (3) , поэтому (3) примет вид
, поэтому (3) примет вид  .
. .
. =
= 
 , где
, где 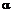 и
и  – углы, образованные касательной в точке
– углы, образованные касательной в точке  с осями
с осями  и
и  соответственно.
соответственно. , т. е. криволинейный интеграл по замкнутому контуру равен площади фигуры ограниченной этим контуром, если
, т. е. криволинейный интеграл по замкнутому контуру равен площади фигуры ограниченной этим контуром, если  .
. 1.
1.  ,
,  , тогда
, тогда 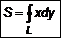 .
. ,
,  , тогда
, тогда  .
. , вдоль которой распределена масса плотностью
, вдоль которой распределена масса плотностью  , тогда ее масса будет определяться выражением
, тогда ее масса будет определяться выражением .
. , а образующая параллельна оси
, а образующая параллельна оси 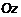 (рис. 4), то площадь поверхности, задаваемой сверху функцией
(рис. 4), то площадь поверхности, задаваемой сверху функцией 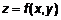 , определяется по формуле
, определяется по формуле  .
. от точки
от точки  до точки
до точки  , если плотность
, если плотность  . Запишем
. Запишем
 .
. – эллипса. Запишем в полярных координатах
– эллипса. Запишем в полярных координатах  , где
, где  . Тогда площадь
. Тогда площадь 
 .
.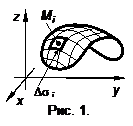 Пусть по криволинейной поверхности
Пусть по криволинейной поверхности  , то
, то  , где
, где  . Предположим, что в пределах выбранной части плотность постоянна и равна
. Предположим, что в пределах выбранной части плотность постоянна и равна  , тогда количество заряда i-той части
, тогда количество заряда i-той части  . Аналогично определим заряды всех частей. Заряд всей поверхности
. Аналогично определим заряды всех частей. Заряд всей поверхности  . Обозначим
. Обозначим  , а точное значение
, а точное значение . (1)
. (1) , (2)
, (2) – дифференциал поверхности.
– дифференциал поверхности. с проекцией
с проекцией  на плоскость
на плоскость  , пересекаемая прямой, параллельной оси
, пересекаемая прямой, параллельной оси  . Обозначим вектор
. Обозначим вектор  как
как  , тогда
, тогда  .
. Касательная площадь определяется как
Касательная площадь определяется как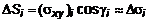 . (3)
. (3) . (4)
. (4)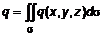 .
. .
. .
. .
. Задача: Необходимо найти поток несжимаемой (
Задача: Необходимо найти поток несжимаемой (  ), стационарно текущей жидкости через поверхность
), стационарно текущей жидкости через поверхность 
 .
. Определение 2.
Определение 2. Выбор стороны поверхности называется ориентацией. За положительную сторону условимся принимать ту, нормаль к которой вместе с положительным направлением на замкнутом контуре образует правый винт (рис. 4).
Выбор стороны поверхности называется ориентацией. За положительную сторону условимся принимать ту, нормаль к которой вместе с положительным направлением на замкнутом контуре образует правый винт (рис. 4). . Разобьем поверхностьна n частей, площади которых обозначим
. Разобьем поверхностьна n частей, площади которых обозначим  . Умножим полученное значение на проекцию i-той части на плоскость
. Умножим полученное значение на проекцию i-той части на плоскость  с учетом ориентации поверхности (вектор нормали в общем случае имеет координаты
с учетом ориентации поверхности (вектор нормали в общем случае имеет координаты  ). Составим сумму
). Составим сумму 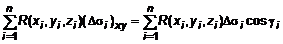 . Найдем предел суммы при
. Найдем предел суммы при  , (7)
, (7)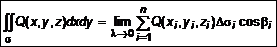 , (8)
, (8) , (9)
, (9)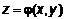 , то выражения (6 – 8) запишем в виде
, то выражения (6 – 8) запишем в виде . (10)
. (10) , (11)
, (11) , (12)
, (12) непрерывно дифференцируемы на гладкой, ограниченной замкнутым контуром
непрерывно дифференцируемы на гладкой, ограниченной замкнутым контуром  . (13)
. (13) . (14)
. (14)