
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лекция 19. Дифференцирование функции многих переменных
План лекции 1. Частные приращения и частные производные функции многих переменных 2. Геометрический смысл частных производных функции многих переменных 3. Дифференцируемость функции многих переменных 4. Полный и частный дифференциалы функций многих переменных 5. Дифференцирование сложных функций 6. Инвариантность дифференциала первого порядка 7. Дифференцирование неявных функций 8. Производные высших порядков функции многих переменных Введение Уже известно, что теория пределов справедлива не только для функции одной переменной, но и для функций многих переменных, следовательно, теория дифференцирования и интегрирования так же должна быть применима для функций многих переменных. Однако вопрос приращения аргумента или аргументов, а также приращение функции оставался пока не изученным. Поскольку приращение можно давать как отдельным переменным, так и в их сочетании, то и производных будет несколько. Этому вопросу и посвящена лекция. Полученные знания будут необходимы для понимания двойных и тройных интегралов, а также теории комплексных функций. Кроме того, в данной лекции рассматриваются вопросы, аналогичные функции одной переменной, по вычислению дифференциалов функций многих переменных, заданных различными способами. 1. Частные приращения и частные производные функции многих переменных Рассмотрим этот вопрос относительно функции двух переменных  Определение 1. Приращение функции, полученное за счет изменения только одной переменной, называется частным
Например, частная производная функции двух переменных по переменной
Аналогичным образом записывается частная производная по любой переменой функции многих переменных. 1.1. Правило дифференцирования Чтобы вычислить частную производную функции многих переменных, надо дифференцировать ее как функцию одной переменной и только этой переменной, а остальные переменные считать постоянными. ПРИМЕР 1. Найти частные производные функции 1. 2. 3. 2. Геометрический смысл частных производных функции многих переменных Пусть задана функция двух переменных
Таким образом, частная производная функции двух переменных есть угловой коэффициент касательной к линии, образованной пересечением графика этой функции с плоскостью, параллельной Замечание!
3. Дифференцируемость функции многих переменных Рассмотрим данный вопрос относительно функции двух переменных Определение 3. Полным приращением функции называется приращение, полученное за счет изменения каждого ее аргумента
ПРИМЕР 2. Найти полное и частные приращения функции 1. 2. 3. Выводы! 1. 2. Определение 4. Функция двух переменных называется дифференцируемой в точке, если ее полное приращение в этой точке имеет вид
 , (4) , (4)
где Теорема 1 (необходимое условие дифференцируемости). Если функция Доказательство. По условию справедливо (4). Пусть переменная Следствия! 1. Полное приращение дифференцируемой функции имеет вид
2. Теорема верна для любого числа переменных. Пусть Замечание! Обратите внимание, что если в
Для того чтобы функция многих переменных была дифференцируема в некоторой точке, необходимо и достаточно, чтобы существовали конечные частные производные в окрестности этой точки, а в самой точке были непрерывны. 4. Полный и частный дифференциалы функций многих переменных Определение 5. Полным дифференциалом функции многих переменных называется главная линейная относительно приращений аргументов часть полного приращения дифференцируемой функции
где Определение 6. Произведение частной производной функции на дифференциал соответствующей переменной называется частным дифференциалом
Сравнивая выражения (6) и (7), запишем
ПРИМЕР 3. Определим дифференциал функции Из (5) следует, что
Погрешность оценки составляет ПРИМЕР 4. Оценить 5. Дифференцирование сложных функций 5.1. Обе переменные зависимые
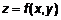 , где , где  и и  – функции независимой переменной – функции независимой переменной  . Напомним (ч. 2, л. 7), что производная сложной функции одной переменной равна . Напомним (ч. 2, л. 7), что производная сложной функции одной переменной равна  . .
Теорема 3. Если функция
Доказательство. Так как ПРИМЕР 5. Дано 5.2. Одна переменная зависимая Пусть
где ПРИМЕР 6.
 и и  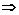  . .
5.3. Обе переменные как функции двух переменных Пусть
6. Инвариантность дифференциала первого порядка Пусть
7. Дифференцирование неявных функций 7.1. Функция двух переменных Уравнение Теорема 4. Если
Доказательство. Пусть задана функция ПРИМЕР 7. Дано 7.2. Функция трех переменных Уравнение
ПРИМЕР 8. Найти 8. Производные высших порядков функции многих переменных
Частные производные от частных производных первого порядка называются частные производные второго порядка или вторыми частными производными.
Аналогично определяются и обозначаются частные производные n-го порядка. Частные производные высших порядков, взятые по различным переменным, называются смешанными производными. Теорема 5. Если функция
ПРИМЕР 9. Для Заключение Введенные ранее теоремы, определения и понятия относительно функции одной переменной являются частным случаем общих понятий для функций многих переменных. Отметим, что: - дифференциал первого порядка функции многих переменных инвариантен; - смешанные производные не зависят от последовательности дифференцирования. - частные производные имеют смысл угловых коэффициентов в сечениях функции; - дифференциал функции одной переменной это приращение касательной прямой, - дифференциал функции двух переменных это приращение касательной плоскости; - выражения дифференциала справедливы для любого числа переменных. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Ростов-на-Дону: Феникс, 1997.– 512 с. 3. Шнейдер В.Е. Краткий курс высшей математики. – М.: ВШ, 1998.
Цель лекции: рассмотреть различные типы практических задач и методы и решения с использованием теории функции многих переменных, научиться находить экстремум функции двух переменных. План лекции |
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 362. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Дадим приращение одной из переменных
. Дадим приращение одной из переменных  . При этом новое значение функции
. При этом новое значение функции  .
. . (1)
. (1) Определение 2.
Определение 2.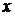 записывается как
записывается как  . (2)
. (2)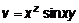 .
. .
. .
. .
. из области определения. Проведем через эту точку секущие плоскости
из области определения. Проведем через эту точку секущие плоскости  и
и  , параллельные координатным плоскостям
, параллельные координатным плоскостям  и
и  . Эти плоскости пересекут поверхность, образуя кривые, описываемые функциями одной переменной
. Эти плоскости пересекут поверхность, образуя кривые, описываемые функциями одной переменной  и
и  соответственно. Определим производные этих функций
соответственно. Определим производные этих функций и
и  .
. и
и  ) к указанным линиям в точке
) к указанным линиям в точке  .
. . При этом новое значение функции
. При этом новое значение функции  .
. . (3)
. (3) .
. .
. .
. .
. .
.  содержит члены, зависящие от
содержит члены, зависящие от  и
и  линейно и нелинейно.
линейно и нелинейно. – функции от переменных
– функции от переменных  , не зависящие от
, не зависящие от  ,
,  – бесконечно малая величина при
– бесконечно малая величина при 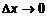 и
и  , стремящаяся к нулю быстрее, чем величина
, стремящаяся к нулю быстрее, чем величина  (т. е. более высокого порядка малости
(т. е. более высокого порядка малости  ).
). и
и  .
. фиксированная, тогда
фиксированная, тогда  . Согласно (4)
. Согласно (4) 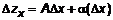 . Определим
. Определим 

 . (5)
. (5) дифференцируема, тогда
дифференцируема, тогда  , где
, где  .
.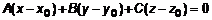 – уравнении плоскости (см ч. 1, л. 11) выразить
– уравнении плоскости (см ч. 1, л. 11) выразить  . Пусть
. Пусть  , тогда получим выражение, схожее с (4). То есть основная часть (4) есть приращение касательной плоскости к поверхности в точке. Напомним, что в уравнении плоскости коэффициенты
, тогда получим выражение, схожее с (4). То есть основная часть (4) есть приращение касательной плоскости к поверхности в точке. Напомним, что в уравнении плоскости коэффициенты  есть координаты вектора нормали к плоскости.
есть координаты вектора нормали к плоскости. , (6)
, (6) – неразделимый символ частной производной.
– неразделимый символ частной производной. ,
,  . (7)
. (7) . (8)
. (8) . Согласно (8)
. Согласно (8)  ,
,  .
. . При малых
. При малых  , т. е.
, т. е.  или
или . (9)
. (9) , где
, где  в области {
в области {  ;
; 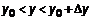 }.
}. с точностью
с точностью  . Представим в выражение в виде функции
. Представим в выражение в виде функции  , при этом
, при этом  и
и  . Тогда
. Тогда 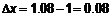 ,
,  . Определим
. Определим 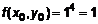 ,
,  и
и  , откуда вычислим
, откуда вычислим  и
и  . Тогда
. Тогда  .
. и по
и по  равна
равна . (10)
. (10) дифференцируема по
дифференцируема по 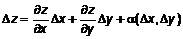 , где
, где  . Найдем
. Найдем 

 , или
, или  , см. (1).
, см. (1). ,
,  ,
, 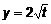 . Определим дифференциал
. Определим дифференциал  .
. , тогда по теореме 1
, тогда по теореме 1 , (11)
, (11) – частная производная,
– частная производная,  – полная производная.
– полная производная. и
и  промежуточные переменные, дифференцируемые по
промежуточные переменные, дифференцируемые по 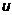 и
и 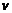 , а
, а  и
и 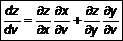 . (12)
. (12) , тогда
, тогда  , пусть
, пусть  . Определим
. Определим 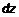 , если
, если 


 .
. . (13)
. (13) задает неявно функцию
задает неявно функцию 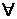
 , то
, то 
 задает неявно
задает неявно  дифференцируема по
дифференцируема по  , то существует производная
, то существует производная . (14)
. (14) . Тогда
. Тогда  – сложная функция и справедливо (11). Подставим в выражение (11) исходную функцию и получим
– сложная функция и справедливо (11). Подставим в выражение (11) исходную функцию и получим  , откуда
, откуда  или
или  .
. . Запишем
. Запишем  . Тогда
. Тогда 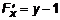 ,
,  и
и  .
. задает неявно функцию
задает неявно функцию  существует единственное значение
существует единственное значение  ;
; 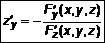 . (15)
. (15) , если
, если  . Запишем
. Запишем  . Определим согласно (15)
. Определим согласно (15)  и
и  . Тогда
. Тогда 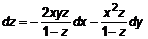 .
.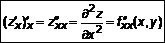 ,
,  .(16)
.(16) .
.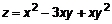 частные производные:
частные производные:  ;
;  ;
;  ;
;  ;
;  ;
;  .
.