
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лекция 23. Тройные интегралыЦель лекции: изучить понятие тройного интеграла; научиться определять тип задач, приводящих к тройному интегралу; вычислять тройной интеграл. 1. Задачи, приводящие к понятию тройного интеграла 2. Определение тройного интеграла 3. Вычисление тройного интеграла в декартовых координатах 4. Замена переменных в тройном интеграле 5. Физические приложения тройного интеграла
В предыдущих лекциях рассматривался двойной интеграл. Тип задач, приводящих к нахождению двукратных интегралов, уже известен. Из примеров было видно, что двойной интеграл не позволяет определять, например, массы неоднородного объемного тела, его момента инерции и др. Ясно, что подобные задачи необходимо решать при помощи трехкратного интеграла, которому посвящена эта лекция. 1. Задачи, приводящие к понятию тройного интеграла 1.1. Задача о массе неоднородного тела
1.2. Другие задачи Аналогичная задача может ставиться о нахождении средней температуры тела. Если  2. Определение тройного интеграла
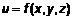 в области в области  пространства пространства  . Разобьем область определения V на n частей, площади которых обозначим . Разобьем область определения V на n частей, площади которых обозначим  . В i-той части выберем произвольную точку . В i-той части выберем произвольную точку  , вычислим в ней значение функции и произведения , вычислим в ней значение функции и произведения  . Составим интегральную сумму всех произведений . Составим интегральную сумму всех произведений  . Найдем предел интегральной суммы при . Найдем предел интегральной суммы при  , где , где 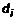 – расстояние между двумя наиболее удаленными точками i-той области или диаметр области. Если этот предел существует и не зависит ни от способа разбиения области V на части, ни от выбора точки в каждой части, то он называется тройным интегралом и обозначается – расстояние между двумя наиболее удаленными точками i-той области или диаметр области. Если этот предел существует и не зависит ни от способа разбиения области V на части, ни от выбора точки в каждой части, то он называется тройным интегралом и обозначается
где V – область интегрирования, Теорема 1 (о существовании тройного интеграла). Если функция 2.1. Свойства тройного интеграла Поскольку тройные интегралы построены по такому же принципу, что и двойные интегралы, то справедливы те же свойства. Теорема 2 (о среднем). Если функция
3. Вычисление тройного интеграла в декартовых координатах 3.1. Переход к декартовым координатам Вычисление двойного интеграла сводится к последовательному вычислению трех определенных интегралов.
 Область определения функции Область определения функции  определяется следующим образом. Объем определяется следующим образом. Объем  ограничен снизу и сверху функциями ограничен снизу и сверху функциями  и и  соответственно. С боков она ограничена цилиндрической поверхностью с образующей соответственно. С боков она ограничена цилиндрической поверхностью с образующей  и направляющей границей области D, как проекцией поверхности на плоскость и направляющей границей области D, как проекцией поверхности на плоскость  . .
Теорема 3. Если функция
Сначала вычисляется внутренний интеграл по переменной z. В результате получаем функцию двух переменных. Если область определения задана как
Замечание! В рассмотренном случае область V была простой, т. е. прямая
3.2. Правило вычисления тройного интеграла Чтобы вычислить тройной интеграл надо привести его к повторному.
2. Спроецировать область интегрирования на плоскость оставшихся переменных. Далее расстановка пределов интегрирования аналогична двукратному интегралу. Вопрос 4. Замена переменных в тройном интеграле 4.1. Правило преобразования Допустим, что для вычисления определенного интеграла необходима замена переменных по следующим формулам:
Напомним, что замена переменных равносильна замене области интегрирования. В данном случае это замена некоторой области в трехмерном пространстве
4.2. Переход к цилиндрическим координатам Как известно, положение точки в трехмерном пространстве можно зафиксировать пересечением трех поверхностей. В цилиндрической системе запишем:
Очевидно, что данную систему можно представить как полярную систему координат
4.3. Переход к сферической системе координат
Согласно геометрии (рис. 5), можно составить уравнения перехода от декартовой к сферической системе координат. Якобиан преобразования:
Вопрос 5. Физические приложения тройного интеграла 5.1. Определение массы неоднородного тела Согласно выражению (1) масса неоднородного тела с плотностью
где границы области определения 5.2. Статистические моменты и координаты центра тяжести тела Координаты центра тяжести системы массой
5.3. Моменты инерции неоднородного тела Моменты инерции относительно координатных плоскостей
относительно координатных осей
а так же относительно начала координат
Заключение Для лучшего усвоения материала рекомендуется прочесть еще раз основные выводы по каждой лекции. Отметим, что все интегральные задачи строятся по одному принципу разбиение и предельный переход». Используя его, можно составлять интегральные задачи любой кратности. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. |
||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 286. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Дано неоднородное объемное тело (рис. 1) с неоднородной плотностью, заданной функцией трех переменных
Дано неоднородное объемное тело (рис. 1) с неоднородной плотностью, заданной функцией трех переменных  . Необходимо определить его массу. Если
. Необходимо определить его массу. Если  , то
, то 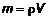 , где
, где  . Возьмем i-тую часть, в которой произвольно выберем точку
. Возьмем i-тую часть, в которой произвольно выберем точку  . Предположим, что в пределах выбранной части плотность постоянна и равна
. Предположим, что в пределах выбранной части плотность постоянна и равна  , тогда масса i-той части
, тогда масса i-той части  . Тогда масса всего тела приближенно определяется интегральной суммой
. Тогда масса всего тела приближенно определяется интегральной суммой  . Обозначим
. Обозначим 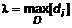 , где за
, где за  . (1)
. (1) – температура тела, тогда средняя температура
– температура тела, тогда средняя температура  ..
.. , (2)
, (2) – подынтегральная функция,
– подынтегральная функция,  – элемент объема в декартовой системе координат
– элемент объема в декартовой системе координат 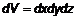 .
. непрерывна в замкнутой ограниченной пространственной области, то существует тройной интеграл функции по этой области.
непрерывна в замкнутой ограниченной пространственной области, то существует тройной интеграл функции по этой области. точка
точка  :
:  , где
, где  – среднее значение функции в V. Из теоремы
– среднее значение функции в V. Из теоремы 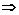
 . (3)
. (3) . (4)
. (4) . (5)
. (5) (рис. 2), то выражение (5), запишем
(рис. 2), то выражение (5), запишем . (6)
. (6) Если область V – параллелепипед, то все пределы постоянны (рис. 3).
Если область V – параллелепипед, то все пределы постоянны (рис. 3). . (8)
. (8) .
. (см. л. 39). Согласно правилу перехода запишем соответствующий якобиан преобразования, и если
(см. л. 39). Согласно правилу перехода запишем соответствующий якобиан преобразования, и если  , то справедливо
, то справедливо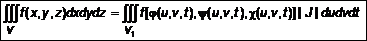 . (9)
. (9)
 – расстояние от точки M поверхности до оси
– расстояние от точки M поверхности до оси 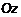 ;
; – плоскость, проходящая через точку M и образующая угол
– плоскость, проходящая через точку M и образующая угол  с плоскостью
с плоскостью  ;
; – плоскость
– плоскость  (рис. 4).
(рис. 4). с дополнительной аппликатой декартовой системы координат
с дополнительной аппликатой декартовой системы координат  , или
, или , тогда
, тогда  и
и  . (10)
. (10)
 ;
; 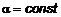 – плоскость, проходящая через точку M и образующая угол
– плоскость, проходящая через точку M и образующая угол 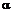 с плоскостью
с плоскостью  – коническая поверхность с вершиной в точке
– коническая поверхность с вершиной в точке  между образующей и осью
между образующей и осью  ,
, 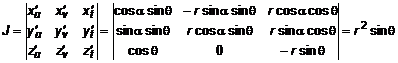 .
. .(11)
.(11) определяется трехкратным интегралом
определяется трехкратным интегралом ,
,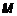 определяются согласно выражениям
определяются согласно выражениям  ,
,  ,
,  . Следуя рассуждениям, используемым в предыдущих лекциях, запишем
. Следуя рассуждениям, используемым в предыдущих лекциях, запишем ;
; 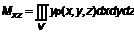 ;
;  .
. ,
, 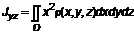 ,
,  ,
, ,
,  ,
,  ,
,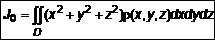 .
.