
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лекция 14. Определенный интегралСтр 1 из 7Следующая ⇒ Лекция 12. Неопределенный интеграл Цель занятия: изучить понятие первообразной, ее геометрический смысл, а также понятие интеграла; научиться находить основные интегралы. План лекции 1. Первообразная функции и ее свойства 2. Неопределенный интеграл и его свойства 3. Правила интегрирования 4. Таблица основных интегралов 5. Непосредственное интегрирование Введение Этой лекцией начинается новая тема высшей математики «Интегральное счисление». Понятие интеграла неразрывно связано с понятием дифференциала. Для его усвоения нужно знать таблицу производных и теорию пределов. Полученные знания в этом разделе часто используются для решения многих прикладных задач, например нахождение среднего значения объема биомассы, среднего значения экономического роста, нахождение объемов и масс тел, площадей различных поверхностей, например географической местности, нахождение длины траектории движения объекта и т. д. 1. Первообразная функции и ее свойства Определение 1.
1.1. Геометрический смысл первообразной
 – уравнение зависимости тангенса угла наклона прямой от – уравнение зависимости тангенса угла наклона прямой от  . Общее уравнение прямой . Общее уравнение прямой  . Поскольку не задан параметр . Поскольку не задан параметр  , одному и тому же значению , одному и тому же значению 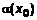 соответствует множество параллельных друг другу прямых (рис. 1). Построим такую кривую соответствует множество параллельных друг другу прямых (рис. 1). Построим такую кривую  , которая в каждой точке , которая в каждой точке  проходила бы таким образом, что указанные прямые с угловым коэффициентом проходила бы таким образом, что указанные прямые с угловым коэффициентом  являлись бы касательными к этой кривой. Эта кривая являлись бы касательными к этой кривой. Эта кривая  и называется первообразной. Поскольку одному значению и называется первообразной. Поскольку одному значению  соответствует множество параллельных друг другу прямых, то таких первообразных может быть построено множество (рис. 2). соответствует множество параллельных друг другу прямых, то таких первообразных может быть построено множество (рис. 2). 1.2. Свойства первообразной Свойство 1. Если Свойство 2. Если Доказательство. Найдем
Если функция имеет первообразную, то она имеет их множество, и все они отличаются на постоянную величину. 2. Неопределенный интеграл и его свойства Определение 2. Множество всех первообразных функций, называется неопределенным интегралом функции и обозначается
где С – постоянная интегрирования. Теорема 1 (существования). Если функция 2.1. Геометрический смысл интеграла Интеграл – это семейство интегральных кривых, полученное смещением одной из кривых вдоль оси 2.2. Свойства интеграла Свойство 1. Дифференциал от интеграла равен подынтегральному выражению Доказательство:
Производная от интеграла равна подынтегральной функции
Доказательство: Свойство 3. Интеграл от дифференциала первообразной равен первообразной Доказательство: Частный случай!
3. Правила интегрирования Правило 1. Постоянный множитель можно выносить и вносить под знак интеграла Доказательство. Производная Правило 2. Неопределенный интеграл от алгебраической суммы конечного числа интегрируемых функций равен алгебраической сумме неопределенных интегралов от каждого слагаемого. Пусть
Доказывается аналогично Правилу 1. 4. Таблица основных интегралов Таблица интегралов получена путем отображения таблицы производных. Чтобы доказать справедливость интеграла, достаточно найти дифференциал правой части и воспользоваться первым свойством интеграла.
Непосредственное интегрирование применяется, когда можно воспользоваться таблицей интегралов или свести интеграл к табличному виду, или внести интегрируемую функцию под знак дифференциала, а затем воспользоваться третьим свойством интеграла. ПРИМЕРЫ. 1. 2. 3. 4. 5.
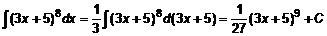 . .
7. 8. 9. 5.1. Преобразование дифференциалов
Заключение Таблица интегралов является справочным материалом и не требует запоминания. Однако важно уметь осуществлять простейшие преобразования подынтегрального выражения с целью дальнейшего непосредственного интегрирования. В конечном счете, к этому сводятся любые методы интегрирования. Приведенные примеры наиболее ярко отражают гибкость таких преобразований. Отметим что: - первообразная функции – это та кривая, у которой тангенсы угла наклона касательных описываются этой функцией; - неопределенный интеграл – это семейство первообразных, отличающихся на постоянную величину; - интеграл от дифференциала дает дифференцируемое выражение плюс С; - константа выносится из-под знака интеграла; - после интегрирования не должно быть других констант кроме С. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – Ростов-на-Дону: Феникс, 1997. – 512 с.
Цель лекции: изучить методы интегрирования, научиться их использовать для нахождения интегралов. План лекции 1. Подстановка 2. Интегрирование по частям 3. Интегрирование рациональных функций 4. Особые методы интегрирования тригонометрических функций 5. Интегрирование иррациональных функций Введение В предыдущей рассматривался самый простой метод интегрирования – непосредственное интегрирование. Однако при решении многих прикладных задач интегрируемая функция зачастую оказывается более сложной и непосредственное интегрирование применить сразу невозможно. Для нахождения таких интегралов существуют различные методы, основная суть которых состоит в том, чтобы более сложную функцию свести к непосредственному интегрированию. 1. Подстановка Теорема 1. Пусть
Доказательство. Найдем производную левой части (1). Согласно второму свойству
Найдем производную правой части (1). По условию
ПРИМЕР 1.
ПРИМЕР 2.
 . .
Обратите внимание, что в предыдущей лекции подобный пример решался непосредственным интегрированием
2. Интегрирование по частям Теорема 2. Если
Доказательство. По правилу 2.1. Правило интегрирования 1. Разбить подынтегральное выражение на два сомножителя, один из которых признать за U, другой за dV. 2. Найти dU и, интегрируя dV, найти V. 3. Записать результат в виде (2). Замечание! Выбирать U необходимо таким образом, чтобы его дифференциал был «проще» изначального выражения. Например, степенная функция. В свою очередь интеграл от dV не должен усложнить выражение. Например, функция ПРИМЕР 3.
2.2. Случаи применения правила 1. Если под интегралом логарифм или его произведение на другую функцию. Принимают 2. Под интегралом обратная тригонометрическая функция или ее произведение на другую функцию. За U принимают обратную тригонометрическую функцию. 3. При интегрировании произведения полинома и указанных функций 4. При интегрировании произведения экспоненциальной функции и тригонометрической.
 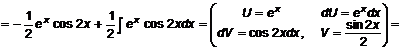
3. Интегрирование рациональных функций Интегралы от некоторых функций не выражаются конечным числом элементарных функций. Например:
Такие интегралы называются не берущимися или неинтегрируемыми в конечном виде и могут быть представлены в виде бесконечной суммы функций. Результат интегрирования – неэлементарная функция. К числу интегралов, выражающихся конечным числом элементарных функций, относятся интегралы от рациональных функций. 3.1. Интегрирование целых рациональных функций
Очевидно, что возможны ситуации, когда невозможно найти первообразную функцию в виде конечной суммы элементарных функций. 3.2. Интегрирование дробных рациональных функций Правильные рациональные дроби, у которых степень числителя меньше степени знаменателя, разлагаются на простейшие дроби. Такие дроби могут быть четырех типов. 1. Правильная дробь I типа 2. Правильная дробь II типа
 . Приведем к виду . Приведем к виду  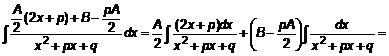 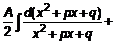 
4. Правильная дробь IV типа
Далее интегрируем по рекуррентной формуле
ПРИМЕР 5.
Интегралы от простейших дробей выражаются через дробно-рациональные функции, логарифм и арктангенс. Так как любая правильная дробь может быть разложена в конечную сумму простейших дробей, то справедлива следующая теорема. Теорема 3. Интеграл от всякой рациональной функции выражается конечной комбинацией элементарных функций.
4.1. Универсальная подстановка, интегралы вида Так как
Это интеграл от рациональной функции. Так как указанная подстановка приводит любую функцию, рациональную относительно тригонометрических функций, к рациональной относительно одной переменной, она называется универсальной. ПРИМЕР 6.
Если ПРИМЕР 7.
4.2. Интегралы вида Если в рациональной зависимости находится только одна тригонометрическая функция, а вторая входит в выражение в первой степени, то можно использовать преобразование
где
где ПРИМЕР 8.
4.3. Интегралы вида 1. Если = ПРИМЕР 9.
2. Если обе степени четные и не отрицательные, то используются формулы понижения степени
ПРИМЕР 10
 , ,  , , 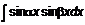
Данные интегралы берутся с использованием формул
ПРИМЕР 11
Используются формулы
ПРИМЕР 12
1. Если степени четные и 2. Если степени нечетные
5. Интегрирование иррациональных функций 5.1. Интегралы вида Пусть общий знаменатель всех показателей
ПРИМЕР 13.
5.2. Интегралы вида Данный интеграл берется аналогично предыдущему. В качестве подстановки используется 5.3. Тригонометрическая подстановка 1. Интеграл вида 2. Интеграл вида
 , то есть , то есть  , ,  , а , а  . .
3. Интеграл вида Заключение Изучены основные и дополнительные методы интегрирования изучили основные и дополнительные методы интегрирования. Строгого запоминания аналитических выражений не требуется. Достаточно знать методы интегрирования. Полученные знания, имеют больше практическое значение, однако они пригодятся и при изучении дифференциальных уравнений. Существуют следующие методы интегрирования: - непосредственное интегрирование; - метод подстановки; - интегрирование по частям; - интегрирование целых и дробных рациональных функций; - особые методы интегрирования рациональной зависимости тригонометрических функций методами универсальной подстановки, а также формулы понижения степени, произведения синусов и др.; - интегрирование иррациональных функций методами тригонометрической и гиперболической подстановки. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Пискунов Н.С. «Дифференциальное и интегральное исчисление». – М.: Высшая школа, 1994. 3. Колмогоров А.Н., Фомин С.В. «Элементы теории функций и функционального анализа» – М.: Наука, 1972. – 496 с. 4. Фихтенгольц Г.М. «Основы математического анализа» Часть 1 – М.: Лань, 2002. - 448 с. 5. Фихтенгольц Г.М. «Основы математического анализа» Часть 2 – М.: Лань, 2002. - 464 с. 6. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление – Ростов-на-Дону: Феникс, 1997. – 512 с. 7. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. – 656 с. Лекция 14. Определенный интеграл Цель лекции: научиться ставить задачи, приводящие к определенному интегралу, изучить свойства определенного интеграла. План лекции 1. Задачи, приводящие к понятию определенного интеграла 2. Определенный интеграл как предел интегральной суммы 3. Условия существования определенного интеграла 4. Свойства определенного интеграла Введение
Данная лекция особенно важна при решения прикладных задач. Например, нахождение объемов, площадей поверхности и др. 1. Задачи, приводящие к понятию определенного интеграла 1.1. Геометрическая задача
Определение 1. Плоская фигура называется квадрируемой, если существуют и равны между собой пределы
Найти длину перемещения материальной точки, движущейся неравномерно прямолинейно со скоростью
2. Определенный интеграл как предел интегральной суммы 1. Пусть 2. Возьмем 3. На каждом отрезке выберем произвольную точку, найдем в ней значение функции и вычислим произведение 4. Составим 5. Выберем Определение 2.
 , если он существует и не зависит ни от способа разбиения отрезка, ни от выбора каждой точки на отрезке, называется определенным интегралом функции на отрезке , если он существует и не зависит ни от способа разбиения отрезка, ни от выбора каждой точки на отрезке, называется определенным интегралом функции на отрезке  и обозначается и обозначается
где Выводы! 1. Определенный интеграл – число, зависящее от подынтегральной функции и от отрезка и не зависящее от переменной интегрирования. 2. Интеграл на отрезке 3. Условия существования определенного интеграла Если существует конечный предел интегральной суммы, не зависящей от Теорема 1 (необходимое условие Если функция Доказательство. Предположим, что в точке
Обратное утверждение не верно. Если функция ограничена, это не значит, что она интегрируема. Например, функция Дирихле Теорема 2 (достаточное условие существования определенного интеграла).
Теорема 3. Если функция ограничена и имеет конечное число точек разрыва первого рода (кусочно-непрерывная), то она интегрируема (рис. 3).
Теорема 4. Если функция ограничена и монотонна на отрезке, то она интегрируема на этом отрезке. Вопрос 4. Свойства определенного интеграла 4.1. Первое свойство Если
Доказательство.
Если функции
Доказательство предлагается провести самостоятельно. Первое и второе свойство – это свойства линейности определенного интеграла. 4.3. Третье свойство аддитивности по промежутку Если
Доказательство сводится к разбиению 4.4. Четвертое свойство Если
Доказательство. Составив интегральную сумму 4.5. Пятое свойство Если функции
Доказательство. По условию
Если
Доказательство. По условию Вывод! Площадь криволинейной трапеции, ограниченной сверху на отрезке ПРИМЕР 1. Оценим величину Заключение К понятию определенного интеграла могут приводить многие прикладные задачи, такие как расчет объема биомассы, определения интегрального среднего экономического роста и др. Отметим, что: - интегральная сумма – это сумма произведений оснований элементарных прямоугольников на их высоты или сумма - определенный интеграл это предел интегральной суммы при условии, что количество прямоугольников бесконечно возрастает; - определенный интеграл это число; - смена пределов интегрирования приводит к смене знака интеграла; - кусочно-непрерывная функция интегрируема; Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Колмогоров А.Н., Фомин С.В. «Элементы теории функций и функционального анализа» – М.: Наука, 1972. – 496 с.
Цель лекции: изучить основные теоремы определенного интеграла, научиться вычислять определенный интеграл. План лекции 1. Теорема о среднем 2. Определенный интеграл как функция верхнего предела 3. Формула Ньютона – Лейбница Введение Из предыдущей лекции ясно, что определенный интеграл – это число. Встает вопрос: «как его определить?». Основное внимание необходимо обратить на формулу Ньютона – Лейбница для вычисления значения определенного интеграла. Знания, полученные на этой лекции, необходимы при решении всех прикладных задач, связанных с нахождением определенного интеграла, вычислении интегрального среднего значения и др. 1. Теорема о среднем Теорема 1. Если
Доказательство. Пусть Частный случай! Если функция непрерывна на
По теореме Больцано – Коши на отрезке Определение 1. Интегральное среднее называется значение функции
2. Определенный интеграл как функция верхнего предела |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 335. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
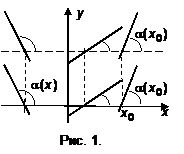 Функция
Функция  на отрезке
на отрезке  (дифференцируема) и
(дифференцируема) и 

 так же первообразная функции
так же первообразная функции  – первообразные функции
– первообразные функции  .
.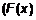


 . Следовательно
. Следовательно 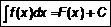 . (1)
. (1) (рис. 2). Поэтому он называется неопределенным
(рис. 2). Поэтому он называется неопределенным . (2)
. (2) .
. .
.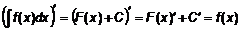 .
. . (3)
. (3) .
. .
. . С другой стороны,
. С другой стороны,  . Следовательно, Правило 1 справедливо.
. Следовательно, Правило 1 справедливо. – интегрируемые функции по переменной
– интегрируемые функции по переменной 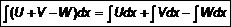 . (4)
. (4)
 ,
,

 ,
, 

 ,
, 
 ,
, 
 ,
, 
 ,
, 

 ,
, 

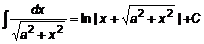 ,
, 
 ,
, 
 .
. .
.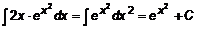 .
. .
. .
. .
. .
. .
. 
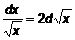










 непрерывно дифференцируема
непрерывно дифференцируема  , тогда
, тогда . (1)
. (1) .
. , t – промежуточная переменная,
, t – промежуточная переменная,  =
= 


 .
. .
. и
и 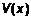 непрерывно дифференцируемы, то
непрерывно дифференцируемы, то . (2)
. (2) , откуда
, откуда 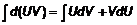 . После интегрирования
. После интегрирования  , откуда
, откуда  .
. . Или наоборот. В итоге подынтегральное выражение должно упроститься.
. Или наоборот. В итоге подынтегральное выражение должно упроститься. .
. .
. . Правило применяется
. Правило применяется  раз.
раз.
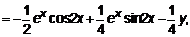 откуда
откуда  .
. ,
,  ,
,  ,
,  ,
,  ,
,  .
.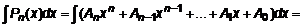


 .
. .
.
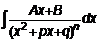 . Приведем к виду
. Приведем к виду 



 +
+  .
. . (3)
. (3) .Вывод!
.Вывод!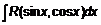
 выражаются рационально относительно
выражаются рационально относительно 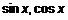 , то рассмотрим интеграл рациональной функции
, то рассмотрим интеграл рациональной функции  . При этом используется универсальная подстановка
. При этом используется универсальная подстановка и
и  .
. .
.

 входят в выражение в четной степени, то удобнее
входят в выражение в четной степени, то удобнее ,
, 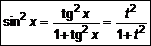 и
и  .
.
 .
.
 ,
, ,
,  , или
, или ,
, ,
,  .
.

 – четное (
– четное (  ), а
), а 
 =
=  =
=  .
. .
. ,
,  ,
,  .
.

 .
.


 4.5. Интегралы вида
4.5. Интегралы вида  ,
, 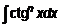 ,
, 
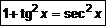 ,
, 


 4.6. Интегралы вида
4.6. Интегралы вида  ,
, 
 , то применяются формулы
, то применяются формулы ,
, .
.
 или
или  , тогда данный интеграл можно записать
, тогда данный интеграл можно записать  . Воспользуемся подстановкой
. Воспользуемся подстановкой  , а
, а  , тогда
, тогда  =
=  .
.


 , где
, где  и подставить в интеграл, далее интегрирование сведется к интегрированию рациональной функции.
и подставить в интеграл, далее интегрирование сведется к интегрированию рациональной функции.  . Используется подстановка
. Используется подстановка  ,
,  или
или  ,
,  . Тогда
. Тогда  . Интеграл сведется к виду
. Интеграл сведется к виду  . Данный интеграл берется согласно правилам, рассмотренным на с. 90 – 92.
. Данный интеграл берется согласно правилам, рассмотренным на с. 90 – 92. . Используется подстановка
. Используется подстановка  или
или  . Кроме того, можно использовать гиперболическую подстановку с учетом выражения
. Кроме того, можно использовать гиперболическую подстановку с учетом выражения  . Используется подстановка
. Используется подстановка  или
или  , тогда
, тогда 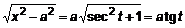 .
. Дана криволинейная трапеция, ограниченная осью
Дана криволинейная трапеция, ограниченная осью  , прямыми
, прямыми  ,
,  и графиком
и графиком  (рис. 1). Необходимо найти площадь. Очевидно, что в криволинейную трапецию могут быть вписаны прямоугольники. Обозначим
(рис. 1). Необходимо найти площадь. Очевидно, что в криволинейную трапецию могут быть вписаны прямоугольники. Обозначим  - последовательность площадей вписанных многоугольников. Последовательность возрастающая и ограниченная сверху. Аналогично обозначим
- последовательность площадей вписанных многоугольников. Последовательность возрастающая и ограниченная сверху. Аналогично обозначим  – последовательность площадей описанных многоугольников. Последовательность убывающая и ограниченная снизу.
– последовательность площадей описанных многоугольников. Последовательность убывающая и ограниченная снизу.  .
.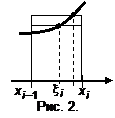 Определим площадь криволинейной трапеции (рис. 1). Для этого разобьем отрезок
Определим площадь криволинейной трапеции (рис. 1). Для этого разобьем отрезок  таким образом, что
таким образом, что  . Система точек
. Система точек  называется разбиением отрезка
называется разбиением отрезка  . Таким образом, площадь разбилась на
. Таким образом, площадь разбилась на  – площадь i-той трапеции. Очевидно, что площадь всей трапеции
– площадь i-той трапеции. Очевидно, что площадь всей трапеции 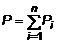 . На отрезке
. На отрезке  выберем произвольную точку
выберем произвольную точку  (рис. 2). Найдем
(рис. 2). Найдем  и примем его за высоту прямоугольника с тем же основанием, что и элементарная трапеция. Тогда приближенно площадь i-той трапеции будет определяться как
и примем его за высоту прямоугольника с тем же основанием, что и элементарная трапеция. Тогда приближенно площадь i-той трапеции будет определяться как  , где
, где  . За
. За  . Так как фигура квадрируема, то существует предел последовательностей площадей вписанных и описанных многоугольников и
. Так как фигура квадрируема, то существует предел последовательностей площадей вписанных и описанных многоугольников и , где
, где  .
. за время
за время  . Разобьем отрезок
. Разобьем отрезок  точками
точками  . В промежутке
. В промежутке  выберем произвольную точку
выберем произвольную точку  , вычислим в этой точке значение скорости
, вычислим в этой точке значение скорости  . Предположим, что скорость за этот промежуток времени не изменилась. Тогда расстояние, пройденное за этот промежуток, определяется
. Предположим, что скорость за этот промежуток времени не изменилась. Тогда расстояние, пройденное за этот промежуток, определяется  , где
, где 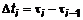 . Такие же предположения сделаем относительно всех промежутков. Тогда общая длина перемещения
. Такие же предположения сделаем относительно всех промежутков. Тогда общая длина перемещения  . Найдем предел
. Найдем предел , где
, где 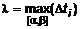 .
. .
.
 .
. – интегральную сумму Римана.
– интегральную сумму Римана.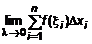 .
. ,
, – пределы интегрирования,
– пределы интегрирования,  .
.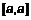 равен нулю. 3.
равен нулю. 3. 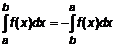 .
. , то функция
, то функция  определенного интеграла).
определенного интеграла). неограниченна. Возьмем
неограниченна. Возьмем  , следовательно,
, следовательно,  . Тогда интегральная сумма
. Тогда интегральная сумма  , а следовательно, и ее предел стремится к
, а следовательно, и ее предел стремится к  .
. . Если за
. Если за  , если за
, если за  . Следовательно, интеграл не существует.
. Следовательно, интеграл не существует. Если функция принадлежит классу интегрируемых функций
Если функция принадлежит классу интегрируемых функций  , где
, где  также интегрируема, то есть постоянный множитель можно выносить за знак интеграла
также интегрируема, то есть постоянный множитель можно выносить за знак интеграла .
.
 интегрируемы на отрезке
интегрируемы на отрезке 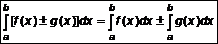 .
. , то
, то .
.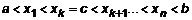 , при этом интегральная сумма
, при этом интегральная сумма  .
. и
и  , то интеграл неотрицательной функции не отрицателен.
, то интеграл неотрицательной функции не отрицателен. .
. и
и  , следовательно,
, следовательно,  .
.
 , то неравенство функций можно интегрировать, т. е.
, то неравенство функций можно интегрировать, т. е. .
. . По 4-му свойству
. По 4-му свойству  . По 2-му свойству
. По 2-му свойству  и
и  .
. , то
, то . (1)
. (1)
 , причем
, причем  , так как
, так как  или
или  . При
. При  придем к (1).
придем к (1). . Определим
. Определим 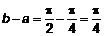 . Функция
. Функция  – убывающая на
– убывающая на  . Наибольшее
. Наибольшее  и наименьшее
и наименьшее  значения. Тогда
значения. Тогда 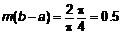 и
и 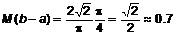 . Следовательно
. Следовательно 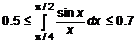
 ;
; 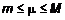 справедливо
справедливо . (1)
. (1)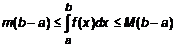 . Разделив обе части на
. Разделив обе части на  , получим
, получим 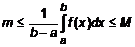 . Обозначим
. Обозначим  , тогда
, тогда  .
. . (2)
. (2) . Подставив значение
. Подставив значение  в (1), получим (4).
в (1), получим (4). . (3)
. (3)