
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лекция 16. Методы вычисления определенного интегралаЦель лекции: научиться применять методы интегрирования для вычисления определенного интеграла, изучить понятие несобственного интеграла и научиться его использовать для нахождения определенного интеграла разрывных функций. План лекции 1. Замена переменной 2. Интегрирование по частям 3. Несобственный интеграл первого типа 4. Несобственный интеграл второго типа 5. Вычисление площадей плоских фигур Введение Поскольку для вычисления определенного интеграла необходимо находить первообразные, то изученные нами ранее правила интегрирования можно использовать для вычисления определенного интеграла. Однако очевидно что, например, при замене переменной меняется не только подынтегральное выражение, но должны меняться и пределы интегрирования. Поэтому на данной лекции рассмотрим известные методы нахождения первообразной для вычисления определенного интеграла. Кроме того, в предыдущей лекции было показано, что вычислить определенный интеграл от разрывных функций известными методами нельзя, поэтому изучим новое понятие несобственного интеграла. 1. Замена переменной Теорема 1. Если
Доказательство.
 – первообразная на – первообразная на  , следовательно, , следовательно,  и и  . Левая часть (1) равна . Левая часть (1) равна  . Докажем, что . Докажем, что 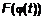 – первообразная для – первообразная для  . По теореме о непрерывности сложной функции . По теореме о непрерывности сложной функции  непрерывна, непрерывна,  непрерывна, непрерывна,  непрерывна. Определим непрерывна. Определим  . Тогда правая часть (1) будет иметь вид . Тогда правая часть (1) будет иметь вид 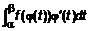 = =   . Следовательно, выражение (1) справедливо. . Следовательно, выражение (1) справедливо.
ПРИМЕР 1.
2. Интегрирование по частям Теорема 2. Если 
Доказательство. По правилу ПРИМЕР 2.
3. Несобственный интеграл первого типа Пусть функция
Определение 2. Несобственным интегралом первого типа с бесконечным нижним пределом называется предел определенного интеграла с переменным нижним пределом при условии, что он стремится в минус бесконечность.
Замечание! Если правые части выражений (3) и (4) существуют и меньше бесконечности, то несобственные интегралы 1-го типа сходятся или существуют. Если
На несобственные интегралы 1-го типа можно обобщить формулу Ньютона – Лейбница
Один нейрон нервной системы был возбужден. После окончания воздействия на него возбуждение начало спадать (функция активации). Расход энергии, затрачиваемой на возбуждение, соответственно уменьшается по экспоненциальному закону
4. Несобственный интеграл первого типа Пусть функция
Несобственным интегралом второго типа от функции, не ограниченной на левом конце интеграла, называется интеграл вида (рис. 3)
Определение 4. Несобственным интегралом второго типа от функции, не ограниченной на правом конце интеграла, называется интеграл вида
Если правые части выражений (6) и (7) существуют и меньше бесконечности, то несобственные интегралы второго типа сходятся или существуют. Если ПРИМЕР 4. Вернемся к интегралу
Из геометрического смысла определенный интеграл – это площадь криволинейной трапеции (рис.6). Однако возможны случаи, когда функция отрицательна, тогда ее необходимо брать по модулю, поскольку площадь должна быть положительна. Более того,
Заключение В заключении отметим, что: - меняя переменную необходимо менять пределы интегрирования; - несобственный интеграл 1-го типа это интеграл с - несобственный интеграл 2-го типа это интеграл с неограниченной функцией в точках пределов интегрирования; - при вычислении плоских фигур необходимо учитывать что определенный интеграл от отрицательной функции будет отрицателен. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление – Ростов-на-Дону: Феникс, 1997. – 512 с.
Цель лекции: рассмотреть прикладные задачи, решение которых основано на интегральном исчислении. План лекции 1. Площадь плоской фигуры в полярных координатах 2. Вычисление длин дуг плоской кривой 3. Вычисление объемов и площадей поверхностей 4. Физические приложения определенного интеграла 5. Работа переменной силы Введение Основная задача этой лекции – рассмотреть дополнительные прикладные задачи, решение которых раскрывает в достаточной мере возможности интегрального исчисления. Данная лекция носит в основном практический характер, несмотря на то, что в ней будут также рассмотрены некоторые новые аналитические выражения. 1. Площадь плоской фигуры в полярных координатах
Криволинейным сектором называется фигура, ограниченная двумя лучами Фигура квадрируема, следовательно, существует площадь этой фигуры. Разобьем сектор на n частных секторов лучами
2. Вычисление длин дуг плоской кривой
 за интервал времени за интервал времени  . Длина пройденного пути определялась как . Длина пройденного пути определялась как  . Данный вывод был очевиден, так как длина всего пути . Данный вывод был очевиден, так как длина всего пути  является пределом бесконечной суммы элементарных участков пути является пределом бесконечной суммы элементарных участков пути  , то есть , то есть  , где , где  . Определим длину дуги в общем случае, заданной уравнением. . Определим длину дуги в общем случае, заданной уравнением.
Пусть кривая линия L задана уравнением
Пусть кривая линия L задана параметрически
Пусть кривая линия L задана в полярных координатах
3. Вычисление объемов и площадей поверхностей 3.1. Объем тела с заданным поперечным сечением
 Пусть в системе координат дано тело. Осуществим поперечное сечение тела плоскостью Пусть в системе координат дано тело. Осуществим поперечное сечение тела плоскостью  . При этом . При этом  будем иметь площадь сечения будем иметь площадь сечения  (рис. 2). Разобьем отрезок (рис. 2). Разобьем отрезок  так, что так, что  , причем , причем  – это i-тая плоскость – это i-тая плоскость  . На отрезке . На отрезке 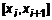 выберем произвольную точку выберем произвольную точку  , проведем через нее произвольное сечение. Пусть , проведем через нее произвольное сечение. Пусть  – площадь сечения, которая не изменяется на всем отрезке – площадь сечения, которая не изменяется на всем отрезке 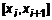 , тогда получим i-й элементарный цилиндр с основанием , тогда получим i-й элементарный цилиндр с основанием  и высотой и высотой  . Объем i-го слоя . Объем i-го слоя 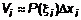 , тогда объем всего тела , тогда объем всего тела  . Перейти к строгому равенству можно, если бесконечно уменьшать высоту элементарного слоя, т.е. . Перейти к строгому равенству можно, если бесконечно уменьшать высоту элементарного слоя, т.е.  , где , где  . Это есть предел интегральной суммы, поэтому . Это есть предел интегральной суммы, поэтому
ПРИМЕР 1. Найти объем пирамиды с площадью основания
 и высотой и высотой  . Очевидно, что справедливо соотношение площадей оснований и высот пирамид . Очевидно, что справедливо соотношение площадей оснований и высот пирамид  , откуда , откуда  и объем пирамиды будет определяться интегралом и объем пирамиды будет определяться интегралом  . .
3.3. Площадь поверхности тела, образованного вращением криволинейной трапеции Пусть задана криволинейная трапеция в плоскости
Выражение (6) приведено для явного задания кривой. Для другого вида задания кривой необходимо учитывать вид 4. Физические приложения определенного интеграла 4.1. Статические моменты
Статическим моментом точки относительно какой-либо оси называется произведение массы на расстояние точки до этой оси (рис. 5).
Определение 3.
4.2. Координаты центра тяжести плоской фигуры
 , или , или  , (7) , (7)
Тогда координаты центра тяжести с учетом
4.3. Координаты центра тяжести дуги Очевидно, что масса дуги будет равна
Координаты центра тяжести будут определяться как
5. Работа переменной силы
 будем считать, что работа не изменяется будем считать, что работа не изменяется  , где , где  . Тогда работа на этом участке будет равна . Тогда работа на этом участке будет равна  , где , где  . Очевидно, что суммарная работа будет определяться как . Очевидно, что суммарная работа будет определяться как  . Переходя к пределу при . Переходя к пределу при  , получим , получим
Заключение Не смотря на то, что в данной лекции рассматривалось практическое приложение определенного интеграла, отметим, что подробное решение классических прикладных задач позволит в будущем правильно ставить подобные задачи и правильно их решать. Для лучшего усвоения рекомендуется еще раз повторить таблицы дифференциалов, интегралов и правила раскрытия неопределенностей. Основное внимание нужно было обратить на различие между понятиями дифференциала дуги и дифференциала переменной, поскольку ошибка, связанная с неправильным определением дифференциала, приведет к неверным результатам. Следует обратить внимание на то, что при определении площади поверхности вращения элементарный участок заменяли не цилиндром, а усеченным конусом. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Пискунов Н.С. «Дифференциальное и интегральное исчисление» – М.: Знание, 1994. 3. Колмогоров А.Н., Фомин С.В. «Элементы теории функций и функционального анализа» – М.: Наука, 1972. – 496 с. 4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление – Ростов-на-Дону: Феникс, 1997. – 512 с. 5. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с.
Цель занятия: изучить понятие «функция многих переменных», понять геометрический смысл и научиться применять теорию пределов к функции многих переменных. План лекции 1. Точечные множества в n-мерном евклидовом пространстве 2. Функции двух и трех переменных, их геометрический смысл 3. Предел и непрерывность функции многих переменных 4. Свойства функций многих переменных на компакте Введение Нам уже знакомо понятие функции на множестве как заданное отношение. Однако ранее рассматривались функции, заданные бинарным отношением, то есть на множестве, образованном декартовым произведением двух множеств, или на декартовой плоскости. С другой стороны, известно, что отношения бывают n-арные, то есть отношение третьего порядка образует множество в трехмерном пространстве, или по аналогии может быть задана функция двух переменных в трехмерном декартовом пространстве и т. д. В действительности окружающий нас мир невозможно описать функцией конечного числа переменных, однако, допустив некоторые ограничения, достаточно точно описать многие физические явления вполне реально, поэтому понимание сути, геометрического и физического смысла функции многих переменных крайне необходимо. В первом вопросе лекции вводятся дополнительные понятия дискретной математики, требующиеся для понимания новой темы. 1. Точечные множества в n-мерном евклидовом пространстве Введем обозначение элемента евклидового пространства как Определение 1. Совокупность точек M евклидового пространства таких, что расстояние от этих точек до точки
  Частные случаи! Частные случаи!
1. В пространстве
3. В пространстве Определение 2. Пусть D – точечное множество в евклидовом пространстве ( Рассмотрим рис. 4. Здесь точка Определение 3. Точка Определение 4. Точка
Множество D, состоящее только из внутренних точек, называется открытым, а состоящее из внутренних и граничных точек называется замкнутым. Определение 6. Множество D называется связным (см. ч. 1, л. 3, опр. 9), если две любые точки этого множества можно соединить линией, полностью принадлежащей этому множеству. ПРИМЕР 1.
Определение 7. Связное, открытое множество называется областью. Связное, замкнутое множество называется замкнутой областью. Определение 8. Точечное множество называется ограниченным, если существует n мерный шар, которому принадлежат все точки этого множества. Определение 9. Замкнутые, ограниченные области называются компактами. Пусть Определение 10. Функцией n переменных называется отображение множества 2. Функции двух и трех переменных, их геометрический смысл 2.1. Функция двух переменных Определение 11. Функцией двух переменных называется отображение множества 2.1. Способы задания функции двух переменных 1. Аналитический способ За область D принимается множество пар ПРИМЕР 2. Дана функция
Изобразим область определения функции в декартовой плоскости (рис. 6). 2. Табличный способ
 Аналогично функции одной переменной функция двух переменных может быть задана таблично, однако при этом таблица задания функции будет иметь вид двумерной матрицы. Аналогично функции одной переменной функция двух переменных может быть задана таблично, однако при этом таблица задания функции будет иметь вид двумерной матрицы.
3. Графический способ
ПРИМЕР 3. Запишем уравнение верхней части полусферы с центром в точке Важно! Графическое изображения функций двух переменных – линии уровня.
Линией уровня называется линия на графике ПРИМЕР 4. Если h – высота местности над уровнем моря, то это будут линии на топографической карте (рис. 9), соответствующие одной и той же высоте (изолинии). 2.2. Функция трех переменных Определение 13. Функцией трех переменных называется отображение множества
 Важно! Важно!
Геометрически область определения функции трех переменных – это пространственное тело. График функции трех переменных Для графического изображения функций трех переменных пользуются поверхностями уровня. Определение 14.
ПРИМЕР 5. Если с – потенциал электрического поля, то поверхности уровня – это эквипотенциальные поверхности, которые наглядно отображают распределение электрического поля в пространстве. Например, поверхностью уровня потенциала поля электрического заряда является сфера ПРИМЕР 6. Функцией трех переменных может быть функция температуры тела или некоторого газа в пространстве, то есть в каждой точке трехмерного пространства может быть задана скалярная величина 3. Предел и непрерывность функции многих переменных Очевидно, что теория пределов должна распространяться и на функции многих переменных. Пусть
Число b называется пределом функции Определение 16. Величина Определение 17. Число b называется пределом функции Вывод! Все основные теоремы о пределах (единственности, основные и т. д.) можно по аналогии перенести на функцию многих переменных. ПРИМЕР 7.
Определение 18. Функция многих переменных называется непрерывной в точке ПРИМЕР 8.
4. Свойства функций многих переменных на компакте Пусть функция
 на компакте на компакте 
1. Если 2. Функция 3. Любое значение между ПРИМЕР 9.
1. Функция ограничена 2. Функция принимает наибольшее 3. Значения функции находятся в интервале Заключение Изучалось понятие функции многих переменных. Для упрощения понимания смысла этого понятия важно обратить внимание на общность базисных определений. Понимание того, что известная ранее функция одной переменной есть лишь частный случай функции многих переменных, позволит с легкостью изучить дифференцирование функций многих переменных, сформировать пространственное мышление. Отметим, что: - дельта-окрестность в, общем виде, это n-мерная сфера; - область может быть замкнутой, но неограниченной; - область определения функции n переменных имеет размерность - функцию трех переменных часто называют пространственной функцией; - известная теория пределов справедлива для функций n переменных. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Фихтенгольц Г.М. «Основы математического анализа» Часть 1 – М.: Лань, 2002. – 448 с. 3. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. – 656 с.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 279. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 непрерывна, а
непрерывна, а 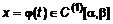 – непрерывно дифференцируема, причем
– непрерывно дифференцируема, причем 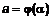 ,
, 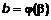 , то
, то . (1)
. (1)
 .
. и
и 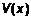
 – непрерывно дифференцируемы, то
– непрерывно дифференцируемы, то . (2)
. (2)
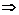
 . Проинтегрируем
. Проинтегрируем  , откуда
, откуда  .
.
 .
. определена на
определена на  , тогда определенный интеграл по этому промежутку не существует (рис. 1).
, тогда определенный интеграл по этому промежутку не существует (рис. 1). Определение 1.
Определение 1. . (3)
. (3) . (4)
. (4) , то несобственный интеграл с двумя бесконечными пределами разбивают на два рассмотренных несобственных интеграла
, то несобственный интеграл с двумя бесконечными пределами разбивают на два рассмотренных несобственных интеграла . (5)
. (5)
 (рис. 2), где
(рис. 2), где  – параметр релаксации нейрона,
– параметр релаксации нейрона,  – начальная энергия, приданная нейрону на возбуждение. Требуется определить полную затраченную на возбуждение нейрона энергию.
– начальная энергия, приданная нейрону на возбуждение. Требуется определить полную затраченную на возбуждение нейрона энергию. 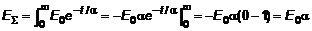
 функция не ограничена.
функция не ограничена.


 Определение 3.
Определение 3. . (6)
. (6)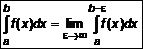 . (7)
. (7) (рис. 4), то интеграл разбивается на два несобственных интеграла второго типа
(рис. 4), то интеграл разбивается на два несобственных интеграла второго типа . (8)
. (8) (рис. 5). Согласно выражению (8)
(рис. 5). Согласно выражению (8)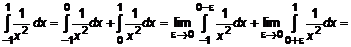

 , хотя площадь под кривой
, хотя площадь под кривой  больше нуля. Это обусловлено переменностью знака функции. Ниже приведены наиболее часто встречающиеся случаи.
больше нуля. Это обусловлено переменностью знака функции. Ниже приведены наиболее часто встречающиеся случаи.

 пределом;
пределом; Определение 1.
Определение 1. ,
,  ,
,  и непрерывной кривой
и непрерывной кривой  (рис. 1), где r и
(рис. 1), где r и  – полярные координаты точек кривой.
– полярные координаты точек кривой.  . Найдем площадь i-того частного сектора. На дуге i-того сектора выберем произвольную точку
. Найдем площадь i-того частного сектора. На дуге i-того сектора выберем произвольную точку  , соединим ее с полюсом и опишем круговой сектор радиуса
, соединим ее с полюсом и опишем круговой сектор радиуса  . Очевидно, что площадь частичного кругового сектора приближенно равна площади частичного криволинейного сектора
. Очевидно, что площадь частичного кругового сектора приближенно равна площади частичного криволинейного сектора  , где
, где  . Аналогично найдем площади всех частичных секторов. Тогда площадь всего криволинейного сектора будет определяться как
. Аналогично найдем площади всех частичных секторов. Тогда площадь всего криволинейного сектора будет определяться как 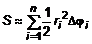 . Обозначим
. Обозначим  , тогда если
, тогда если 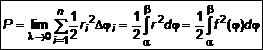 . (1)
. (1) . Требуется определить длину дуги на отрезке
. Требуется определить длину дуги на отрезке  . По теореме Пифагора
. По теореме Пифагора  , откуда определим
, откуда определим  . Тогда длина дуги будет определяться выражением
. Тогда длина дуги будет определяться выражением 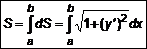 . (2)
. (2) . Требуется определить длину дуги при
. Требуется определить длину дуги при 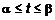 . По теореме Пифагора
. По теореме Пифагора 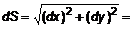
 . Тогда длина дуги будет определяться как
. Тогда длина дуги будет определяться как . (3)
. (3) – полярные координаты. Требуется определить длину дуги при
– полярные координаты. Требуется определить длину дуги при  . По теореме Пифагора
. По теореме Пифагора 


 . Тогда длина дуги будет определяться как
. Тогда длина дуги будет определяться как .
.  . (4)
. (4) (рис. 3). Сечение пирамиды плоскостью
(рис. 3). Сечение пирамиды плоскостью  3.2. Объем тела, образованного вращением криволинейной трапеции
3.2. Объем тела, образованного вращением криволинейной трапеции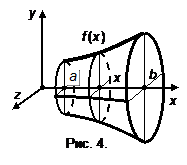 Пусть задана криволинейная трапеция в плоскости
Пусть задана криволинейная трапеция в плоскости  , т. е. фигура ограниченная прямыми
, т. е. фигура ограниченная прямыми  , осью
, осью  . Тогда объем фигуры вращения
. Тогда объем фигуры вращения . (5)
. (5) и
и  . Тогда площадь поверхности усеченного конуса будет определятся как
. Тогда площадь поверхности усеченного конуса будет определятся как 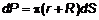 . С учетом, что
. С учетом, что  более высокого порядка малости, запишем
более высокого порядка малости, запишем  , тогда площадь поверхности вращения будет определятся как
, тогда площадь поверхности вращения будет определятся как . (6)
. (6) (см. п. 2).
(см. п. 2). Определение 2.
Определение 2. ,
,  .
. Статическим моментом системы точек называется сумма статических моментов точек этой системы (рис. 6)
Статическим моментом системы точек называется сумма статических моментов точек этой системы (рис. 6) ,
, 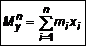 .
. Координаты центра тяжести системы массой
Координаты центра тяжести системы массой 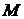 определяются согласно выражениям
определяются согласно выражениям  ,
,  . Пусть криволинейная трапеция (рис. 7) – это плоская фигура с постоянной плотностью
. Пусть криволинейная трапеция (рис. 7) – это плоская фигура с постоянной плотностью  . Для вычисления координат применим интегральный метод. Разобьем отрезок
. Для вычисления координат применим интегральный метод. Разобьем отрезок  . В каждой i-той частной трапеции выберем середину
. В каждой i-той частной трапеции выберем середину  основания
основания  . Заменим элементарную трапецию эквивалентным прямоугольником с высотой
. Заменим элементарную трапецию эквивалентным прямоугольником с высотой  . Очевидно, что координаты центра тяжести прямоугольника с равномерной плотностью будут расположены в серединах этих прямоугольников
. Очевидно, что координаты центра тяжести прямоугольника с равномерной плотностью будут расположены в серединах этих прямоугольников  . Тогда статистические моменты системы точек
. Тогда статистические моменты системы точек 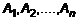 будут определяться согласно
будут определяться согласно , или
, или  . (8)
. (8) могут быть определены согласно выражениям
могут быть определены согласно выражениям ,
,  . (9)
. (9) , где
, где  – линейная плотность. В свою очередь координаты центра тяжести элементарного участка дуги
– линейная плотность. В свою очередь координаты центра тяжести элементарного участка дуги  . Тогда
. Тогда , или
, или  , (10)
, (10) , или
, или  . (11)
. (11) ,
,  . (12)
. (12) Пусть
Пусть  – переменная сила. Очевидно, что работа
– переменная сила. Очевидно, что работа 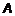 будет зависеть от начала
будет зависеть от начала  и конца
и конца  участка. Применим интегральный метод.
участка. Применим интегральный метод. . (13)
. (13) или
или  , или
, или  , или
, или  .
.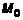 меньше некоторой величины
меньше некоторой величины  , называется дельта-окрестностью
, называется дельта-окрестностью  точки
точки  .
.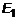 для точки
для точки 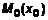 геометрическая интерпретация
геометрическая интерпретация 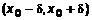 .
.
 2. В пространстве
2. В пространстве 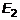 для точки
для точки 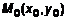 геометрическая интерпретация
геометрическая интерпретация  для точки
для точки  геометрическая интерпретация
геометрическая интерпретация  ), тогда точка
), тогда точка 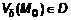 .
. и
и  нет.
нет. содержит хотя бы одну точку этого множества. Совокупность всех граничных точек D называется границей этого множества.
содержит хотя бы одну точку этого множества. Совокупность всех граничных точек D называется границей этого множества.  , которой не принадлежит ни одна точка этого множества.
, которой не принадлежит ни одна точка этого множества.  Определение 5.
Определение 5. соответствует определенное действительное число, то говорят, что на множестве D задана функция n переменных
соответствует определенное действительное число, то говорят, что на множестве D задана функция n переменных  .
. и обозначается
и обозначается  или
или  , где D – область определения, E – область значений.
, где D – область определения, E – область значений. на множество
на множество 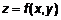 .
. , для которых функция определена. Записывается аналогично функции одной переменной.
, для которых функция определена. Записывается аналогично функции одной переменной. , найти область определения. Очевидно, что
, найти область определения. Очевидно, что  и
и  , тогда область D зададим как
, тогда область D зададим как

 Для любой точки
Для любой точки  задается значение функции
задается значение функции  (рис. 7). Каждой точке из области определения D соответствует точка в пространстве
(рис. 7). Каждой точке из области определения D соответствует точка в пространстве  .
. и радиусом 1 в виде
и радиусом 1 в виде  (рис. 8).
(рис. 8).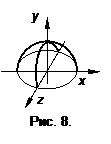 Определение 12.
Определение 12. .
. на множество
на множество 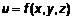 , где D – множество упорядоченных троек чисел
, где D – множество упорядоченных троек чисел  или область определения.
или область определения. Поверхностью уровня называется поверхность, в каждой точке которой функция
Поверхностью уровня называется поверхность, в каждой точке которой функция  .
. (рис. 10) .
(рис. 10) . . Используя поверхности уровня, моделируют небесные тела, планеты, звезды и др. В биологических задачах моделирования широко используются изотермические поверхности и др.
. Используя поверхности уровня, моделируют небесные тела, планеты, звезды и др. В биологических задачах моделирования широко используются изотермические поверхности и др. .
. , если для любого сколь угодно малого положительного
, если для любого сколь угодно малого положительного  найдется другое положительное число
найдется другое положительное число  выполняется условие
выполняется условие  , или
, или 
 .
. есть бесконечно малая в точке
есть бесконечно малая в точке  .
.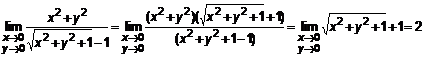
 . Если нарушается какое-либо условие, то функция имеет разрыв в точке.
. Если нарушается какое-либо условие, то функция имеет разрыв в точке.  ; z – не определена при
; z – не определена при  или при
или при  , то есть гипербола – линия разрыва функции.
, то есть гипербола – линия разрыва функции.  , где
, где  и
и  .
. значения.
значения. .
.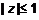 .
. и наименьшее
и наименьшее  значения.
значения. .
. ;
;