
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Касательная плоскость и нормаль к поверхностиЭкстремум функции многих переменных Наибольшее и наименьшее значение функции на компакте Введение В этой лекции разрешаются основные практические задачи, наглядно отображающие физический и геометрический смысл дифференциала функции многих переменных. Материал этой лекции необходим при решении прикладных задач, таких как моделирование поверхностей, анализ поверхностей уровня, программирование образов, кроме того, при определении максимума или минимума роста биомассы, концентрации озона в атмосфере, количества вещества в химических процессах и др. Касательная плоскость и нормаль к поверхности Поверхность задана неявным уравнением
Определение 1. Точка Определение 2. Поверхность, состоящая только из обыкновенных, точек называется гладкой. ПРИМЕР 1. Дана поверхность
Прямая l называется касательной к поверхности
Все касательные прямые в обыкновенной точке принадлежат одной плоскости. Доказательство. Задан годограф (рис. 1)
некоторой векторной функции 
Левая часть (2) есть скалярное произведение векторов.Здесь Определение 4. Плоскость, в которой лежат все касательные прямые, называется касательной плоскостью с вектором нормали
Тогда уравнение касательной плоскости
Определение 5. Нормалью к поверхности в точке называется прямая, перпендикулярная к касательной плоскости в этой точке. Тогда уравнение нормали к поверхности точке
Дана поверхность
и уравнение нормали в точке
Замечание! Очевидно, что в особой точке нет касательной плоскости. 2. Экстремум функции многих переменных Необходимое условие экстремума Определение 6. Точка Определение 7. Точка Теорема 2 (необходимое условие экстремума).
ПРИМЕР 2. Задана поверхность
Точки, в которых частные производные функции равны нулю, называются критическими точками или подозрительными на экстремум. Теорема 3. Если функция то |
||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 273. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Дана поверхность
Дана поверхность  – график неявно заданной функции двух переменных
– график неявно заданной функции двух переменных  . (1)
. (1) называется обыкновенной, если в этой точке существуют частные производные функции и хотя бы одна из них неравна нулю. В противном случае точка называется особая.
называется обыкновенной, если в этой точке существуют частные производные функции и хотя бы одна из них неравна нулю. В противном случае точка называется особая.  . Тогда
. Тогда  . Определим
. Определим  ,
,  ,
,  . Очевидно, что в точке O(0,0,0) частные производные
. Очевидно, что в точке O(0,0,0) частные производные 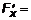

 , поэтому точка O(0,0,0) – особая, а поверхность не гладкая.
, поэтому точка O(0,0,0) – особая, а поверхность не гладкая.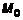 , если она является касательной к любой кривой, лежащей на этой поверхности и проходящей через эту точку (рис. 1).
, если она является касательной к любой кривой, лежащей на этой поверхности и проходящей через эту точку (рис. 1).  Теорема 1.
Теорема 1. .
. . Касательный вектор
. Касательный вектор  . Так как
. Так как  , подставим уравнение 1 в (1)
, подставим уравнение 1 в (1) 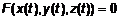 . Продифференцируем последнее по t
. Продифференцируем последнее по t  . (2)
. (2) касательный вектор к L. Обозначим вектор
касательный вектор к L. Обозначим вектор  . Согласно (2)
. Согласно (2)  или
или  . То же можно сказать о любой касательной, проведенной через точку
. То же можно сказать о любой касательной, проведенной через точку  .
. в точке
в точке  . (3)
. (3) . (4)
. (4)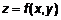 . Определим уравнения касательной плоскости и нормали. Перейдем к неявному виду
. Определим уравнения касательной плоскости и нормали. Перейдем к неявному виду  . Тогда
. Тогда  ,
, 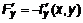 и
и  . Подставим частные производные в (3) и (4) и получим уравнение касательной плоскости
. Подставим частные производные в (3) и (4) и получим уравнение касательной плоскости . (5)
. (5) . (4)
. (4) из области определения D функции
из области определения D функции  этой точки, что для любых
этой точки, что для любых 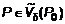 следует
следует  .
. .
. Если функция
Если функция  . Обратное утверждение не верно.
. Обратное утверждение не верно. . Это гиперболический параболоид (рис.2). Определим частные производные
. Это гиперболический параболоид (рис.2). Определим частные производные  ,
,  . Очевидно, что в точке O(0,0) график поверхности не имеет экстремум, но
. Очевидно, что в точке O(0,0) график поверхности не имеет экстремум, но  .
.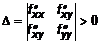 ,
, , то это точка максимума, а если
, то это точка максимума, а если  , то это точка минимума. Если определитель
, то это точка минимума. Если определитель  , то экстремума нет, а если
, то экстремума нет, а если 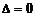 , то сомнительный случай. Необходимо исследовать знак
, то сомнительный случай. Необходимо исследовать знак  при переходе через эту точку.
при переходе через эту точку.