
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Особенности геометрии косозубых, шевронных и конических передач
У косозубых колес различают окружной шаг Pt(в торцовом сечении), нормальный шаг Pn ( в нормальном сечении) и соответственно кружной (торцовый) модуль Стандартным расчетным модулем является нормальный модуль, т.е. m=mn. Очевидны следующие соотношения:
Зацепление косозубых колес в торцовом сечении аналогично зацеплению прямозубых колес. Поэтому геометрический расчет косозубых колеc производится по формулам для прямозубых колес с подстановкой в них параметров торцового сечения. Например, диаметры делительных окружностей определяются по формулам
В косозубой передаче каждый зуб входит в зацепление не сразу по всей длине, а постепенно. Для передач (
Угол наклона линии зуба назначают β=8-15º, для шевронных β = 30-45°. Менее 8° <β выполнять не следует, так как утрачиваются преимущества косозубых передач перед прямозубыми.
Особенности геометрии конических колес
 Так как зубья на боковых поверхностях конусов отличаются от зубьев цилиндрических колес тем, что их размеры (толщина, высота) по мере приближения к вершине конуса уменьшаются, то соответственно изменяются шаг и модуль зацепления, а также и диаметры вершин, делительный и впадин зубьев. Основные параметры зацепления конической прямозубой передачи
где
где Внешнее конусное расстояние
Модуль Диаметры вершин зубьев и впадин конического зубчатого колеса:
Передаточное число при
Среднее конусное расстояние
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 860. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Развернем на плоскость поверхность делительного цилиндра. Угол β называется углом наклона линии зуба. Два колеса в зацеплении должны иметь одинаковые углы β, причем при внешнем зацеплении направление винтовых линий у них разное(на одном колесе – правое, а на другом – левое).
Развернем на плоскость поверхность делительного цилиндра. Угол β называется углом наклона линии зуба. Два колеса в зацеплении должны иметь одинаковые углы β, причем при внешнем зацеплении направление винтовых линий у них разное(на одном колесе – правое, а на другом – левое).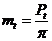 , нормальный модуль
, нормальный модуль 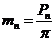 .
.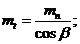 (21.7)
(21.7)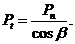 (21.8)
(21.8) (21.9)
(21.9) ) X1 = Х2 = 0
) X1 = Х2 = 0 (21.10)
(21.10)
 . Угол между осями (межосевой угол) теоретически может быть в диапазоне 10°<
. Угол между осями (межосевой угол) теоретически может быть в диапазоне 10°<  <170º. Наибольшее распространение получили передачи с углом
<170º. Наибольшее распространение получили передачи с углом  и
и 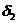 – углы делительного конуса ш.и.к. Конические прямозубые колеса нарезаются на зуборезных станках инструментами, в основу которых положен зуб исходной рейки (ГОСТ 13754-81,
– углы делительного конуса ш.и.к. Конические прямозубые колеса нарезаются на зуборезных станках инструментами, в основу которых положен зуб исходной рейки (ГОСТ 13754-81,  = 1;
= 1; 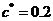 ;
; 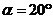 ).
). (21.11)
(21.11) – средний делительный диаметр; de - внешний делительный диаметр; Z– число зубьев ш.и.к;
– средний делительный диаметр; de - внешний делительный диаметр; Z– число зубьев ш.и.к; 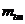 – средний окружной модуль;
– средний окружной модуль;  –внешний окружной модуль, значения которого согласуют с СТ СЭВ 310-76, ГОСТ13755-81.
–внешний окружной модуль, значения которого согласуют с СТ СЭВ 310-76, ГОСТ13755-81. (21.12)
(21.12)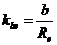 –коэффициент ширины зубчатого венца;
–коэффициент ширины зубчатого венца;  –ширина зубчатого венца;
–ширина зубчатого венца;  –внешнее конусное расстояние.
–внешнее конусное расстояние.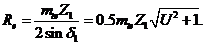 (21.13)
(21.13) и ножки
и ножки 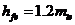 .
. (21.14)
(21.14) (21.15)
(21.15)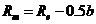 (21.16)
(21.16)