
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задачи и методы кинематического анализа механизмов. Масштабные коэффициентыКинематический анализ механизма состоит в определении движения его звеньев по заданному движению начальных звеньев. При этом считается известной кинематическая схема механизма, т.е. его структурная схема с указанием размеров звеньев, необходимых для кинематического анализа. Основные задачи кинематического анализа. 1. Определение положений звеньев и траекторий отдельных точек звеньев. 2.Определение линейных скоростей и ускорений точек, угловых скоростей и ускорений звеньев. 3. Определение передаточных отношений между звеньями. Эти задачи могут решаться графическими, аналитическими и экспериментальными методами.
Масштабные коэффициенты Масштабным коэффициентом называется отношение численного значения физической величины к длине отрезка в мм, изображающего эту величину. Например, если длина звена равна Масштабный коэффициент скоростей
Построение положений рычажных механизмов методом засечек
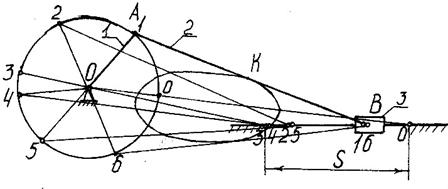
Кинематический анализ механизмов выполняется в порядке присоединения структурных групп. Построение положений плоских механизмов второго класса обычно выполняется методом засечек. В качестве примера рассмотрим кривошипно-ползунный механизм (рис.14.1).
Вначале находим крайние положения механизма (0 и 3), в которых кривошип 1 и шатун 2 располагаются на одной прямой. Для этого из центра 0 делаем засечки радиусами АВ + ОА и АB - ОА на линии движения ползуна 3. Далее делим окружность, описываемую точкой А, на равные части (например, на шесть) и отмечаем последовательные положения точки А – 0, 1, 2, 3, 4, 5, 6, а затем методом засечек на линии движения ползуна получаем последовательные положения точки В – 0, 1, 2, 3 (движение справа налево) 4,5, 6 (движение слева направо). S – ход ползуна. В результате получаем последовательные положения всех звеньев механизма.  Траектория некоторой точки К шатуна получается, если все последовательные положения точки соединить плавной кривой.
Определение скоростей и ускорений рычажных механизмов методом планов
Пример. Кривошипно-ползунный механизм (рис. 14.2). Дано: Формула строения: Построение плана скоростей. Скорость точки А начального звена равна
где
Рассматриваем структурную группу (2, 3). Для определения скорости точки B составляем векторное уравнение согласно теореме о плоскопараллельном движении:
Уравнение (14.1) решаем графически. Для этого из полюса Р откладываем отрезок pa в направлении вектора
Для определения направления угловой скорости Скорость точки K шатуна находим на основании векторных уравнений
где
Отметим основные свойства планов скоростей. 1. Векторы абсолютных скоростей начинаются в полюсе плана. 2. Векторы относительных скоростей соединяют концы векторов абсолютных скоростей, причем вектор на плане направлен к той точке, которая стоит первой в индексе, например, 3. Теорема подобия. Отрезки относительных скоростей точек, принадлежащих одному звену, образуют фигуру, подобную соответствующей фигуре звена и сходственно с нею расположенную. Сходственное расположение означает, что направления обхода одноименных контуров совпадают (например, а-в-ки А-В-К – по часовой стрелке). В рассмотренном примере Построение плана ускорений. Ускорение точки А начального звена
где
причем вектор Выбираем масштабный коэффициент ускорений
Рассматриваем структурную группу (2, 3). Для определения ускорения точки В составляем векторное уравнение согласно теореме о плоскопараллельном движении:
где
Отрезок, изображающий
Уравнение (14.2) решаем графически. Для этого из точки a откладываем отрезок
Для определения направления углового ускорения Ускорение точки K находим на основании теоремы подобия, которая справедлива и для плана ускорений. Для этого методом засечек строим
откуда
В результате получим
Основные свойства планов ускорений такие же, как и планов скоростей.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 920. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
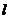 = 0,05 м, а отрезок, изображающий это звено, равен AB= 50 мм, то масштабный коэффициент длин
= 0,05 м, а отрезок, изображающий это звено, равен AB= 50 мм, то масштабный коэффициент длин 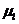 = 0,05/50 = 0,001 м/мм, что соответствует чертежному масштабу 1:1; если же,
= 0,05/50 = 0,001 м/мм, что соответствует чертежному масштабу 1:1; если же, 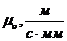 . Если скорость некоторой точки А равна
. Если скорость некоторой точки А равна 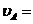 10 м/с, а отрезок, изображающий
10 м/с, а отрезок, изображающий 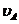 , равен pa=50 мм, то
, равен pa=50 мм, то 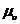 =10/50 = 0,2
=10/50 = 0,2 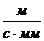 . Масштабный коэффициент ускорений
. Масштабный коэффициент ускорений 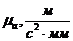 .
.
 = 60 рад/с или
= 60 рад/с или  = 50 об/мин,
= 50 об/мин, 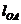 = 100 мм,
= 100 мм, 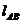 = 300 мм,
= 300 мм, 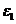 =5 рад/с2.
=5 рад/с2.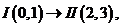 механизм второго класса.
механизм второго класса.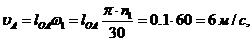
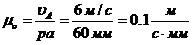
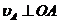 в сторону
в сторону 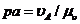 мм, изображающий
мм, изображающий 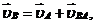 (14.1)
(14.1)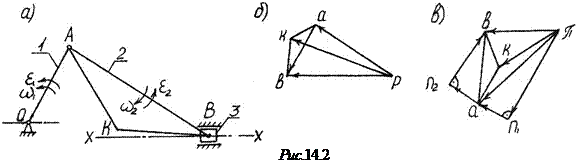 где
где 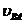 – скорость точки В во вращательном движении звена 2 относительно точки А,
– скорость точки В во вращательном движении звена 2 относительно точки А, 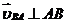 ,
, 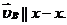
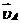 , из точки a проводим прямую в направлении вектора
, из точки a проводим прямую в направлении вектора 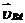 , т.е.
, т.е. 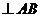 , затем из полюса Р проводим прямую в направлении суммарного вектора
, затем из полюса Р проводим прямую в направлении суммарного вектора 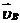 , т.е.
, т.е. 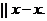 Пересечение указанных направлений дает точку в. В результате находим
Пересечение указанных направлений дает точку в. В результате находим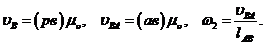
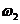 шатуна 2 переносим вектор относительной скорости
шатуна 2 переносим вектор относительной скорости 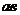 )в точку В и наблюдаем, в какую сторону он поворачивает звено 2 относительно точки А.
)в точку В и наблюдаем, в какую сторону он поворачивает звено 2 относительно точки А.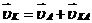 и
и 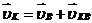
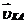 и
и 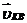 –относительные скорости, причем
–относительные скорости, причем 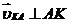 ,
, 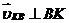 .В результате получим
.В результате получим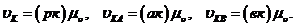
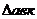 ~
~ 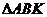 .
.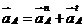
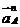 –нормальное ускорение;
–нормальное ускорение;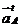 – касательное (тангенциальное) ускорение.
– касательное (тангенциальное) ускорение.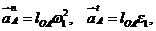
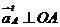 в сторону
в сторону 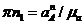 мм, изображающий
мм, изображающий 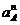 , и отрезок
, и отрезок 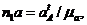 мм, изображающий
мм, изображающий 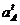 . Точка
. Точка 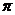 – полюс плана ускорений. Откладываем отрезки
– полюс плана ускорений. Откладываем отрезки 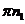 и
и 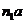 в соответствии с их направлениями. Тогда
в соответствии с их направлениями. Тогда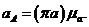
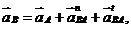 (14.2)
(14.2)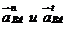 –нормальная и касательная составляющие ускорения
–нормальная и касательная составляющие ускорения 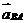 точки В во вращательном движении звена 2 относительно точки А, причем вектор
точки В во вращательном движении звена 2 относительно точки А, причем вектор 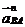 направлен вдоль АВ от В к А, а
направлен вдоль АВ от В к А, а 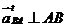 . Нормальная составляющая находится также по величине
. Нормальная составляющая находится также по величине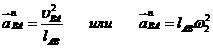
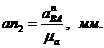
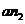 в направлении вектора
в направлении вектора 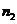 проводим прямую в направлении вектора
проводим прямую в направлении вектора 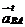 , а из полюса
, а из полюса 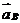 , т.е.
, т.е. 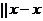 . Пересечение указанных направлений дает точку в. В результате находим
. Пересечение указанных направлений дает точку в. В результате находим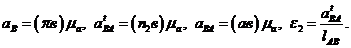
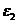 шатуна 2 переносим вектор касательного ускорения
шатуна 2 переносим вектор касательного ускорения 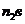 ) точку В и наблюдаем, в какую сторону он поворачивает звено 2 относительно точки А.
) точку В и наблюдаем, в какую сторону он поворачивает звено 2 относительно точки А.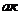 и
и 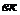 находим из пропорций
находим из пропорций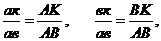
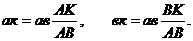
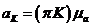 .
.