
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
В матричном виде система уравнений (6.5) запишется более компактно⇐ ПредыдущаяСтр 13 из 13
В линейных системах этот вектор линейно связан с вектором состояния:
Управляемость САУ. Критерий управляемости системы по Калману. Управляемость — одно из важнейших свойств системы управления, описывающее возможность перевести систему из одного состояния в другое. Состояние Система называется полностью управляемой, если все компоненты её вектора состояний управляемы. Условия Р.Калмана позволяют оценить свойства систем управления, такие как: управляемость, наблюдаемость и чувствительность. Для линейных систем существует критерий управляемости в пространстве состояний. Пусть существует система порядка 
Где
здесь Простые критерии проверки управляемости и наблюдаемости системы основаны на анализе матрицы управляемости NУ=[B | AB | A2B | ... | An-1B] Необходимым и достаточным условием управляемости системы является невырожденность матрицы управляемости detNУ |
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 393. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (6.6)
(6.6) - вектор переменных состояний:
- вектор переменных состояний:  ;
; - вектор управления :
- вектор управления :  ;
;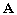 - матрица параметров размера (
- матрица параметров размера (  );
); - матрица управления размера (
- матрица управления размера ( 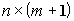 ):
): ,
,  .
.
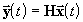 (6.7)
(6.7) .
. (6.8)
(6.8) линейной системы управляемо, если существует такой вход
линейной системы управляемо, если существует такой вход  , который переводил бы начальное состояние
, который переводил бы начальное состояние  в конечное состояние
в конечное состояние  (начало координат) за конечный интервал времени
(начало координат) за конечный интервал времени  .
.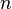 (с
(с 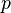 входами и
входами и  выходами, записанная в виде:
выходами, записанная в виде: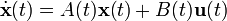

 ;
;  ;
;  ;
; ,
,  ,
,  ,
,  ,
,  .
. — «вектор состояния»,
— «вектор состояния»,  — «вектор выхода»,
— «вектор выхода»,  — «вектор входа»,
— «вектор входа»,  — «матрица системы»,
— «матрица системы», 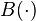 — «матрица входа»,
— «матрица входа»,  — «матрица управления»,
— «матрица управления»,  — «сквозная матрица».
— «сквозная матрица». 0, что эквивалентно условию равенства ранга матрицы NУ порядку n системы, то есть rank NУ = n. Если rank NУ < n, то система неполностью управляемая; если rank NУ = 0 система полностью неуправляемая.
0, что эквивалентно условию равенства ранга матрицы NУ порядку n системы, то есть rank NУ = n. Если rank NУ < n, то система неполностью управляемая; если rank NУ = 0 система полностью неуправляемая.