Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Оценка устойчивости САУ по распределению корней характеристического уравнения на плоскости корней.Чтобы понимать по таким графикам устойчива система или достаточно знать,что если хоть один корень (pk(n) ) находится справа от оси (y) то такая система является уже не устойчивой,если же все корни собраны слева, то система будет устойчивой.
Собственное (свободное) движение системы Свободное движение системы (элемента) содержит апериодические и колебательные составляющие. Первые определяются действительными корнями характеристического уравнения R (p) = 0, а вторые - парами сопряженных комплексных корней. Время затухания свободной составляющей переходного процесса определяется величиной Оценка устойчивости системы по Гурвицу. Матрица коэффициентов характеристического уравнения, ее анализ. Оценка устойчивости системы по Гурвицу формулирует условие устойчивости в виде определителей. Для нахождения условий устойчивости системы n-го порядка по коэффициентам характеристического уравнения сначала составляют матрицу, действуя в следующим порядке. По главной диагонали матрицы (слева вниз направо) последовательно выписывают коэффициенты характеристического уравнения, начиная с a1. Столбцы матрицы, начиная с главной диагонали, заполняют коэффициентами характеристического уравнения вверх по возрастанию индексов до а n , а вниз – по их убыванию до a0. Оставшиеся пустыми места заполняют нулями. Если система имеет n-й порядок, то всего должно быть заполнено n строк и n столбцов матрицы. 
Затем из матрицы выделяют диагональные определители или определители Гурвица; для этого в ней отчеркивают одинаковое число строк и столбцов, начиная от левого угла матрицы. Определители Гурвица имеют вид: Δ1=а1; Δ2= По алгебраическому критерию линейная система n-го порядка устойчива, если коэффициент а0 и все n диагональных определителей Гурвица положительны. Положительность определения n-го порядка обычно не выделяют, так как он может быть представлен произведением Δn=an* Δn-1 И следовательно, требование его положительности свободного члена характеристического уровня an и предпоследнего определителя Δn-1. Управляемость динамических систем. В классической теории управляющие воздействия (управления) определялись как воздействия, оказываемые со стороны регулятора на объект с целью обеспечения его желаемого функционирования . При этом неявно предполагалось, что воздействия u(t) способны обеспечить требуемый характер изменений управляемых величин. На самом деле, это не всегда так. В связи с данным обстоятельством в современной ТАУ введено строгое определение управляемости. Нужно заметить, что существуют несколько понятий, формализующих это фундаментальное свойство ДС. Ниже рассматривается наиболее часто встречающееся. Для этого нужно вновь вернуться к матрично-векторной ММ ДС X = A * X + B * U + G * V ( 1) Определение управляемости ДС. Объект как ДС с ММ (1) называется полностью (вполне) управляемым, если для любого начального состояния X0 = X(t0) существует (ничем не ограниченное) управление U(t) , которое переводит этот объект в любое конечное состояние X1 = X (t1) за конечное время t = t1 – t0 . Нужно обратить внимание, что данное определение управляемости требует только возможности перевода объекта из одного произвольного состояния в другое произвольное, причем за конечное время. При этом совершенно не важен вид траектории, по которой совершается перевод, а также характер поведения объекта при t > t0. Кроме того, необходимо учесть, что под понятие ДС попадает и ОУ и САУ. Поэтому данное определение применимо и к технологическому объекту, и к технической системе, и к системе автоматического управления, для которой внешним является задающее воздействие. Управляемость объектов обычно исследуется с помощью сформулированного ниже критерия, предложенного Калманом , и основывающегося на анализе свойств специальным образом сконструированной матрицы управляемости. Определение матрицы управляемости. Матрица, построенная на основе системной матрицы и матрицы управляющих входов ДС (1) по формуле Mu = [B I AB I .. I A(n-1)B ] (2) называется «матрицей управляемости» данной ДС. Критерий управляемости ДС по Калману. ДС (1) с матрицей управляемости Mu , построенной по правилу (2) и имеющей ранг r = rank (Mu ) (3) является: а) полностью (вполне) управляемой, если r =n ; б) частично (не вполне) управляемой, если 0<r<n (при этом r = n – d,где d- дефект матрицы Mu ); в) полностью (вполне) неуправляемой, если r=0 (d=n ). Из формулы (2) следует, что управляемость ДС (1) зависит только от свойств матриц A и B ее МВ ММ. Поэтому во многих источниках говорится об управляемости пары ( A , B ). Следует сделать замечание по поводу размерности матрицы Mu и связанных с нею особенностях применения критерия. Она имеет, в общем случае, размер (n x n *r) , где r – размерность вектора управлений. Поэтому, если объект имеет несколько управлений, то матрица Mu является прямоугольной. Если же управление одновходовое, т.е. скалярное, то матрица управляемости является квадратной. Тогда в данном частном случае критерий управляемости принимает следующий вид: det(Mu) = I Mu I не равно 0 (4) Иными словами, для полной управляемости одновходового объекта (пары ( A , B ), где B – столбец) необходимо и достаточно, чтобы матрица управляемости, построенная по формуле (2), была не особая (невырожденная). Следует заметить, что при исследовании многовходовых ДС часто имеет смысл проанализировать не только их общую управляемость по вектор-входу, но и управляемость отдельных каналов. Это целесообразно по разным причинам. Во-первых, не редки случаи, когда один или часть входов объекта обеспечивают его полную управляемость. Тогда не имеет смысла усложнять схему и закон управления, и можно построить САУ с использованием меньшего, чем r , количества управляющих воздействий. Во-вторых, такое исследование позволяет выделить наименее и наиболее эффективные каналы управления. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 486. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
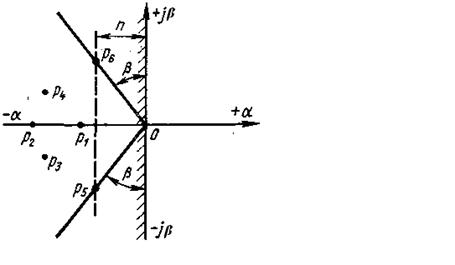
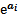 , где ai – величина , обратная постоянной времени затухания Ti. Можно считать, что длительность этой составляющей ti=(приблизительно)3Ti. Отсюда следует, что для сокращения времени переходного процесса необходимо стремиться к увеличению вещественной части корней характеристического уравнения. Колебательная составляющая определяется выражение Cieаitsin(Bit+ фi), где Bi- мнимая часть корня, ti=
, где ai – величина , обратная постоянной времени затухания Ti. Можно считать, что длительность этой составляющей ti=(приблизительно)3Ti. Отсюда следует, что для сокращения времени переходного процесса необходимо стремиться к увеличению вещественной части корней характеристического уравнения. Колебательная составляющая определяется выражение Cieаitsin(Bit+ фi), где Bi- мнимая часть корня, ti= 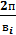 – период колебаний.
– период колебаний.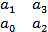 Δ3=
Δ3=