
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Составить уравнение движения АСР с устойчивым объектом 1го порядка без запаздывания с пропорциональным регулятором.
Пусть элементы системы регулирования (рис. 1.1) с П- регулятором описываются следующими уравнениями: ОР: ИП: y = АР: u = ИУ: v = Составим уравнение динамики автоматической системы регулирования. Для этого подставим уравнения элементов АСР в уравнение OP. Получим:
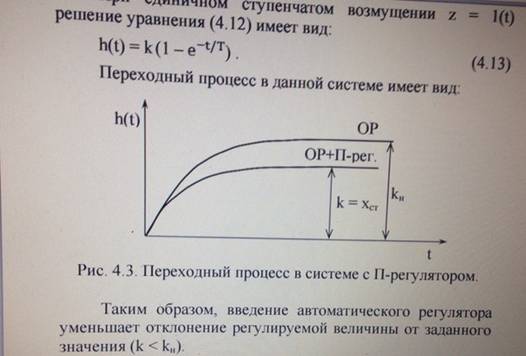
Т где Т = При единичном ступенчатом возмущении z = 1(t) h(t) = k (1 – Для ОР при ступенчатом возмущении z =1(t): х = Для системы регулирования:
Таким образом, введение автоматического регулятора уменьшает отклонение регулируемой величины от заданного значения (k < kн). Выводы: 1. Пропорциональный регулятор всегда приводит систему к равновесию. 2. Главный недостаток П-регулятора – наличие в системе регулирования статической ошибки регулирования xст. Она уменьшается с увеличением коэффициента усиления регулятора kр. 3. Скорость изменения выходной величины в ОР и в АСР в начальный момент времени одинаковы. Составить уравнение движения АСР с устойчивым объектом 1го порядка без запаздывания с ПД-регулятором
ОР: ИП: y = АР: u = ИУ: v = Подставив уравнения элементов АСР в уравнение ОР получим:
Т где Т = При ступенчатом возмущении z = 1(t) h(t) = k (1 – Найдем скорость изменения выходной величины в системе регулирования в начальный момент времени:
Очевидно, что 
Составить уравнение движения АСР с устойчивым объектом 1го порядка без запаздывания и пропорционально-интегральным регулятором
Составить уравнения движения АСР С нейтральным объектом 1го порядка без запаздывания и пропорциональным регулятором
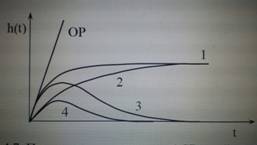
Переходные процессы в АСР с нейтральным объектом 1-го порядка: С ПД-регулятором Пусть элементы системы регулирования описываются следующими уравнениями: ОР: Т0(dx/dt)+x= kнz–k0v ИП: y= kипx АР: u= kpy+ Тд(dy/dt) ИУ: v= kиуu Подставив уравнения элементов АСР в уравнение ОР получим: Т0(dx/dt)+x= kнz–k0kиу(kp kипx+ Тдkип(dx/dt)); Т0(dx/dt)+k0kиуkpkипx+ k0kиуТдkип(dx/dt)+ х =kнz; Т(dx/dt)+x= kz, где Т = (T0+ k0kиуkипTд)/( 1+k0kиуkрkип) ; k=(kн/(1+k0kиуkрkип). При ступенчатом возмущении z=1(t) h(t) = k(1 – e-t/T) . Найдем скорость изменения выходной величины в системе регулирования в начальный момент времени: (dx/dt)=k*1/T*e-t/T; при t = 0. (dx/dt)=k/T=(kн/(1+k0kиуkрkип))/((T0+ k0kиуkипTд)/( 1+k0kиуkрkип))=kн/(T0+ k0kиуkипkр) Очевидно, что (dxacp/dt)< (dxOp/dt). Вывод: введение Д - составляющей уменьшает начальную скорость изменения выходной величины системы регулирования. Статическая ошибка регулирования в системе с ПД-регулятором такая же, как и в системе с П-регулятором |
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 513. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
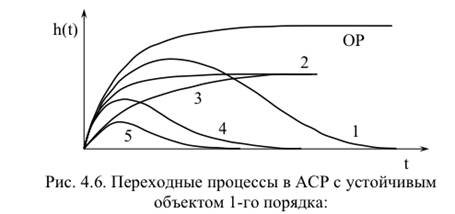 2- с П-регулятором
2- с П-регулятором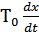 + x =
+ x = 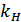 z –
z – 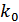 v ;
v ;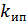 x ;
x ;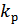 y ;
y ;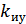 u .
u .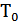
 + x =
+ x = 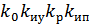 x ;
x ;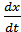 + x = kz,
+ x = kz,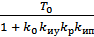 ; k=
; k= 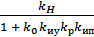
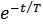 )
)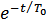 );
); 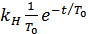 ; при t = 0
; при t = 0 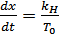
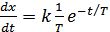 ; при t=0
; при t=0  =
= 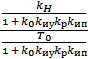 =
= 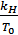
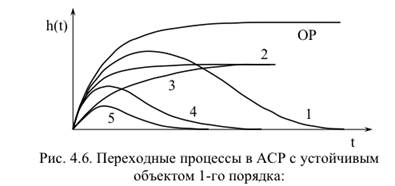 3- с ПД-регулятором
3- с ПД-регулятором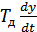 ;
;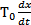 + x =
+ x = 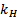 z –(
z –( 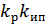 x + Тд
x + Тд 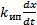 )
)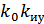 Тд
Тд 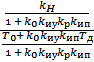 =
= 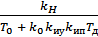
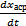 <
< 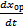 . Вывод: введение Д- составляющей уменьшает начальную скорость изменения 56 выходной величины системы регулирования. Статическая ошибка регулирования в системе с ПД-регулятором такая же, как и в системе с П-регулятором
. Вывод: введение Д- составляющей уменьшает начальную скорость изменения 56 выходной величины системы регулирования. Статическая ошибка регулирования в системе с ПД-регулятором такая же, как и в системе с П-регулятором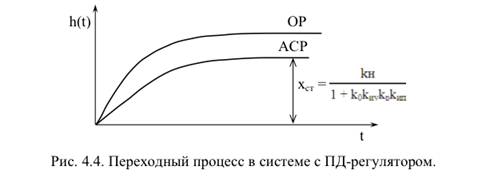






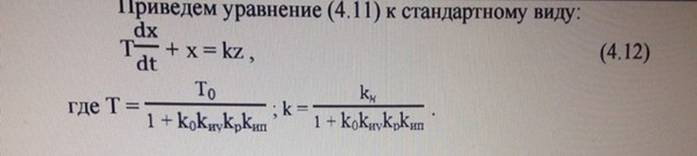
 33.Составить уравнение движения АСР с нейтральным объектом 1го порядка без запаздывания и пропорционально-дифференциальным регулятором.
33.Составить уравнение движения АСР с нейтральным объектом 1го порядка без запаздывания и пропорционально-дифференциальным регулятором.