
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Проверка гипотезы о нормальном распределении случайной величины по критерию ПирсонаДля проверки гипотезы о нормальном распределении случайной величины Х сравнивают между собой экспериментальные и теоретические частоты по критерию Пирсона:
Критерий Пирсона определяет меру расхождения между выборочными данными и теоретическими, определяемыми в соответствии с высказанной гипотезой о распределении случайной величины Х. Если экспериментальные вероятности pi совпадут с теоретическими Статистика В теории математической статистики оказывается, что проверку гипотезы о модели закона распределения по критерию Пирсона можно делать только в том случае, если выполняются следующие неравенства: n>50, Из результатов вычислении, приведённых в таблице 1.7 следует, что необходимое условие для применения критерия согласия Пирсона не выполнены, т.к. в некоторых группах При уменьшении числа групп для теоретических частот соответственно уменьшают и число групп для эмпирических частот. После объединения групп в формуле для числа степеней свободы V=k-3 в качестве k принимают  новое число групп, полученное после объединения частот. Результаты объединения интервалов и теоретических частот приведены в таблице 1.5. Таблица 1.5 - Результаты объединения интервалов и теоретических частот
Результаты вычислений из таблицы 1.5 можно используют для проверки гипотезы о нормальном распределении с помощью критерия Пирсона. Процедура проверки гипотезы о нормальном распределении случайной величины Х выполняется в следующей последовательности: 1. Задаёмся уровнем значимости
2. Вычисляем наблюдаемое число критерия, используя экспериментальные и теоретические частоты из таблицы 1.5
3. Для выбранного уровня значимости k – число групп эмпирического распределения. 4. Сравнивают фактически наблюдаемое А) Если Б) Если При выбранном уровне значимости В результате получаем: Для
Следовательно, выдвинутая гипотеза о теоретическом законе распределения не противоречит выборке наблюдений при заданном уровне значимости, т.е. нет оснований отвергать гипотезу о нормальном распределении. При выбранном уровне значимости
Следовательно, нет оснований отвергать гипотезу о нормальном распределении при заданном уровне значимости При выбранном уровне значимости
Следовательно, нет оснований отвергать гипотезу о нормальном распределении при заданном уровне значимости При выбранном уровне значимости
Следовательно, выдвинутая гипотеза о теоретическом законе распределения не противоречит выборке наблюдений при заданном уровне значимости, т.е. нет оснований отвергать гипотезу при выборочном уровне значимости
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 293. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
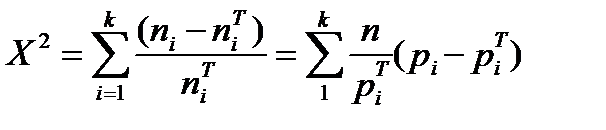 (1.33)
(1.33)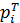 , то значение x2 равно нулю. Чем ближе значение x2 к нулю, тем с большей вероятностью можно будет принять гипотезу о предполагаемом распределении.
, то значение x2 равно нулю. Чем ближе значение x2 к нулю, тем с большей вероятностью можно будет принять гипотезу о предполагаемом распределении. имеет распределение с V=k-r-1 степенями свободы, где число k – число интервалов эмпирического распределения, r – число параметров теоретического распределения, вычисленных по экспериментальным данным. Для нормального распределения число степеней свободы равно V=k-3.
имеет распределение с V=k-r-1 степенями свободы, где число k – число интервалов эмпирического распределения, r – число параметров теоретического распределения, вычисленных по экспериментальным данным. Для нормального распределения число степеней свободы равно V=k-3.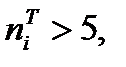 где i=1,2,3,…
где i=1,2,3,… . Поэтому те группы вариационного ряда, для которых необходимое условие не выполняется, объединяют с соседними и, соответственно, уменьшают число групп, при этом частоты объединённых групп суммируются. Так объединяют все группы с частотами
. Поэтому те группы вариационного ряда, для которых необходимое условие не выполняется, объединяют с соседними и, соответственно, уменьшают число групп, при этом частоты объединённых групп суммируются. Так объединяют все группы с частотами  до тех пор, пока для каждой новой группы не выполнится условие
до тех пор, пока для каждой новой группы не выполнится условие  .
.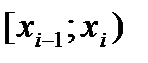
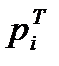
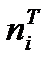
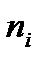

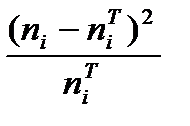
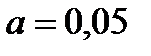 или одним из следующих значений
или одним из следующих значений ,
,  ,
,  .
.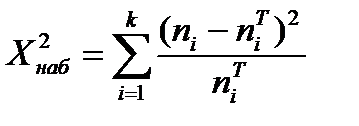
 по таблице распределения находят критические значения
по таблице распределения находят критические значения  при числе степеней свободы V=k-3, где
при числе степеней свободы V=k-3, где критическим
критическим  , то выдвинутая гипотеза о теоретическом законе распределения отвергается при заданном уровне значимости.
, то выдвинутая гипотеза о теоретическом законе распределения отвергается при заданном уровне значимости. , то выдвинутая гипотеза о теоретическом законе распределения не противоречит выборке наблюдений при заданном уровне значимости, т.е. нет оснований отвергать гипотезу о нормальном распределении, т.к. эмпирические и теоретическое частоты различаются незначительно (случайно).
, то выдвинутая гипотеза о теоретическом законе распределения не противоречит выборке наблюдений при заданном уровне значимости, т.е. нет оснований отвергать гипотезу о нормальном распределении, т.к. эмпирические и теоретическое частоты различаются незначительно (случайно). 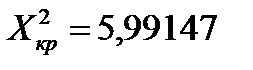 .
. , которое нашли по результатам вычислений, приведённых в таблице 1.8, имеем
, которое нашли по результатам вычислений, приведённых в таблице 1.8, имеем


