
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Ранжирование выборочных данных, вычисление моды и медианы
Используя исходные данные, запишем все заданные значения выборки в виде неубывающей последовательности значений случайной величины X, представленные в табл.1.2.
Таблица 1.2 - Ранжированный ряд
Интервал [31,17; 53,68], содержащий все элементы выборки, разобьём на частичные интервалы, используя при этом формулу Стерджеса для определения оптимальной длины и границ этих частичных интервалов. По формуле Стерджеса длина частичного интервала равна: Вычисляем границы интервалов: За начало первого интервала принимаем значение
Далее вычисляем границы интервалов:
Вычисление границ заканчивается, как только выполняется неравенство После определения частичных интервалов, определяем экспериментальные частоты ni , равные числу членов вариационного ряда, попадающих в этот интервал: xi-1 ≤ x(s) < xi , (1.16)  где xi-1, xi – границы i-го интервала; x(s) – значения вариационного ряда. Набор частот n1,n2,…, nk должен удовлетворять равенству: n1 + n2 +…+ nk = Относительной частотой Wi называют долю наблюдений, попадающих в рассматриваемый интервал: Wi = Плотность распределения относительных частот определим как отношение относительных частот к величине интервала:
где Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны эмпирической плотности распределения: ͡pi = где i=1,2,…, k. Площадь i-го прямоугольника равна доле случайных величин, попавших в i-й интервал: Si = ͡pi h = Площадь гистограммы относительных частот равна сумме площадей прямоугольников: S = Таким образом, функция Полигоном относительных частот называется ломаная линия с вершинами в точках: По результатам вычислений составим табл.1.3 значений выборочной функции плотности. В первую строку таблицы поместим частичные интервалы, во вторую строку – середины интервалов, в третью строку запишем частоты – количество элементов выборки, попавших в каждый частичный интервал, в четвёртую строку запишем относительные частоты, в пятую строку запишем значения плотности относительных частот или значения выборочной, экспериментальной функции плотности. Таблица 1.3 - Значения выборочной функции плотности
По результатам вычислений функции плотности, представленной в таблице 1.3 можно сделать вывод, что в интервалах [39,32; 42,58) и [42,58; 45,84) больше всего элементов – по 17 в каждом. Объедим эти интервалы в один и вычислим моду: мода имеет один локальный максимум в окрестностях точки х = 44,21 с частотой ni = 18. Оценку медианы находим, используя вариационный ряд, для которого n = 2k = 60 и k = 30:
Сравнение оценок медианы |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 281. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1.14)
(1.14) (1.15)
(1.15)








 , то есть
, то есть  .
. = n (1.17)
= n (1.17)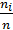 (1.18)
(1.18) , (1.19)
, (1.19)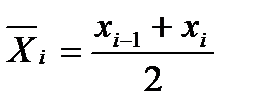 является серединой интервала [xi-1; xi).
является серединой интервала [xi-1; xi). , (1.20)
, (1.20) (1.21)
(1.21) (1.22)
(1.22) является статистическим аналогом плотности распределения случайной величины Х, реализации которой получают при статистическом наблюдении. Полигоном частот называется ломаная линия, отрезки которой соединяют середины горизонтальных отрезков, образующих прямоугольники в гистограмме.
является статистическим аналогом плотности распределения случайной величины Х, реализации которой получают при статистическом наблюдении. Полигоном частот называется ломаная линия, отрезки которой соединяют середины горизонтальных отрезков, образующих прямоугольники в гистограмме. (1.23)
(1.23) 
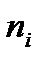



 (1.24)
(1.24)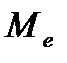 = 42,05 и оценки математического ожидания
= 42,05 и оценки математического ожидания  показывает, что они отличаются на 0,997%.
показывает, что они отличаются на 0,997%.