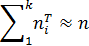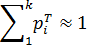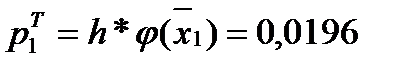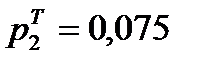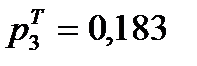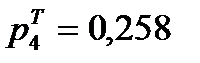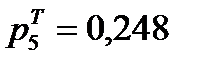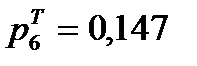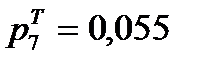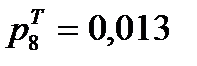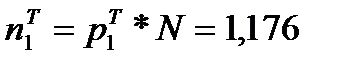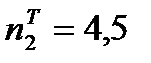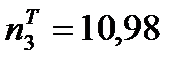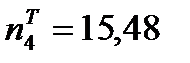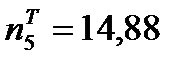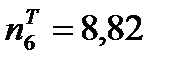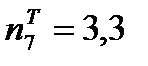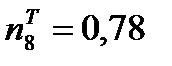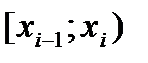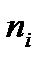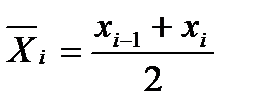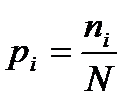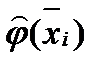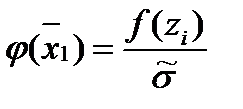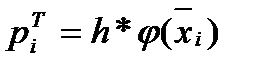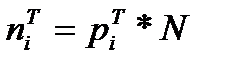Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Параметрическая оценка функции плотности распределенияИсходя из гипотезы, что заданная выборка имеет нормальный закон распределения, найдём параметрическую оценку функции плотности, используя формулу для плотности распределения вероятности нормального закона
где
Значения этой функции вычисляют для середин частичных интервалов вариационного ряда, т.е. при
Для этого вычисляем значения
Затем по таблице находим значение
И после вычисляем функцию
Функция φ(х) принимает наибольшее значение при x = X :
Если h мало и объём выборки n велик, то можно приближенно, достаточно близко определить вероятность того, что случайная величина Х принадлежит интервалу [xi-1;xi), по формуле: P где Используем соотношение, связывающее теоретическую вероятность
Тогда теоретические частоты 
Может оказаться, что теоретические частоты числами, но число элементов выборки, попадающих в i-й интервал, всегда является целым числом. Поэтому округлим дробные теоретические частоты до целых значений с условием, чтобы сумма всех найденных теоретических частот была близка к n:
Если сумма теоретических вероятностей существенно ниже единицы, то надо построить дополнительные интервалы слева и справа от основного интервала [x0; xk). Для средних значений частичных интервалов, построенных слева и справа от интервала [x0; xk), вычислим значения теоретической плотности нормального распределения и теоретические частоты. Сумма для всех теоретических вероятностей должна быть близка к единице с точностью до нескольких знаков после запятой:
Вычислим теоретические вероятности:
Вычислим теоретические частоты:
Результаты вычислений вероятностей и соответствующих частот приведены в таблице 1.4. В первом столбце таблицы расположены k частичных интервалов, во втором столбце расположены наблюдаемые частоты ni , в третьем столбце расположены координаты середины частичных интервалов, в четвёртом столбце расположены относительные частоты, в пятом столбце расположены значения экспериментальной функции плотности, в шестом столбце расположены значения zi , в седьмом столбце расположены значения теоретической функции плотности, вычисленные в середине частичных интервалов, в восьмом столбце расположены значения теоретических вероятностей, в девятом столбце расположены значения теоретических частот. Таблица 1.4 - Результаты вычисления экспериментальных и теоретических вероятностей и частот
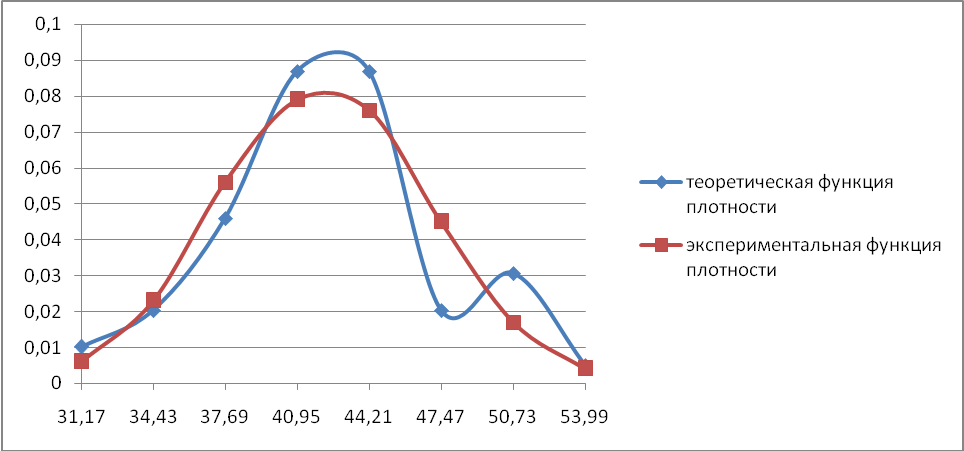
Построим графики экспериментальной и теоретической плотности нормального распределения (рис. 1)
Рис.1.Теоретическая и экспериментальная функции плотности вероятностей
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 304. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
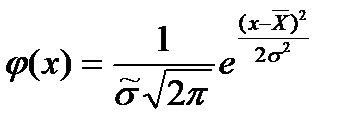 , (1.25)
, (1.25)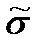 и
и 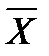 известны – они вычисляются по выборке.
известны – они вычисляются по выборке.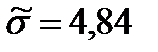
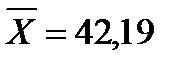
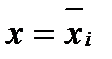 . На практике для упрощения вычислений функции
. На практике для упрощения вычислений функции 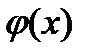 , где i=1,2,…,k, пользуются таблицами значений функции плотности стандартной нормальной величины (Приложение В).
, где i=1,2,…,k, пользуются таблицами значений функции плотности стандартной нормальной величины (Приложение В).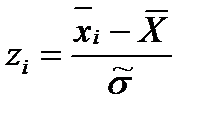 для i=1,2,…,k: (1.26)
для i=1,2,…,k: (1.26) 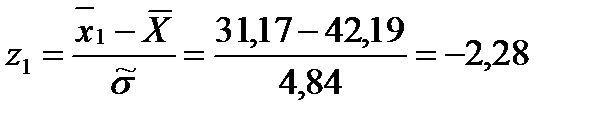
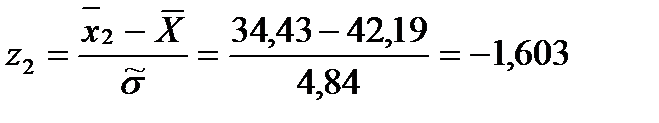
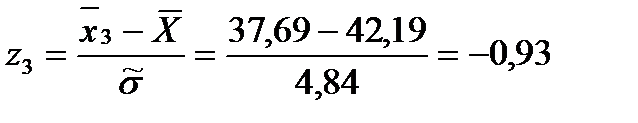
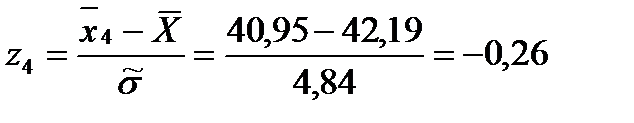
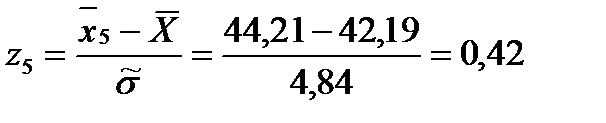
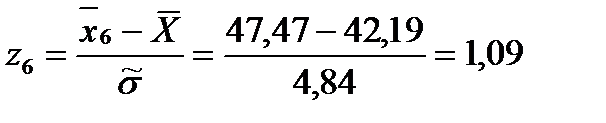
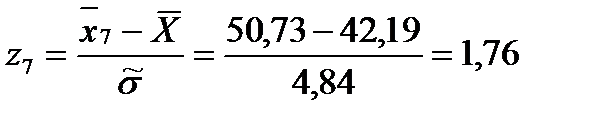
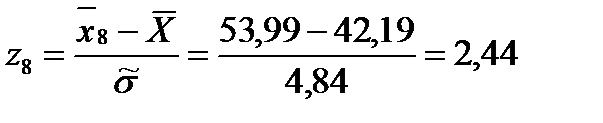
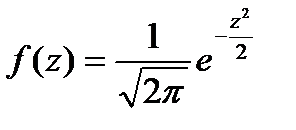 : (1.27)
: (1.27)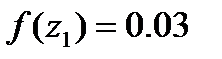
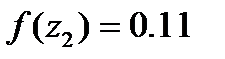
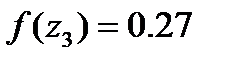
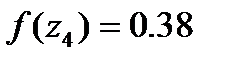
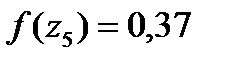
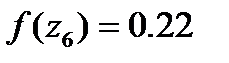
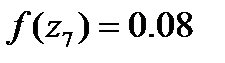
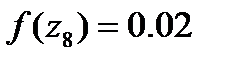
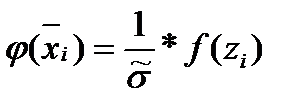 : (1.28)
: (1.28)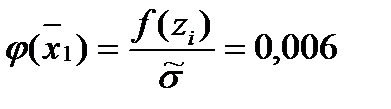
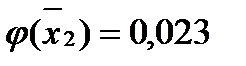
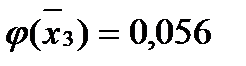
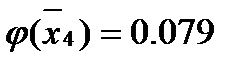
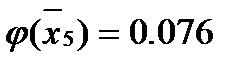
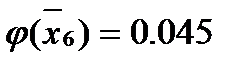
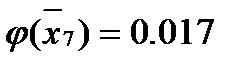
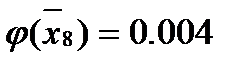
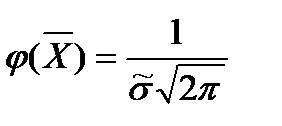 (1.29)
(1.29)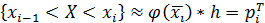 , (1.30)
, (1.30)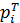 – теоретическая вероятность.
– теоретическая вероятность.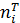 :
: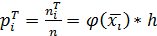 (1.31)
(1.31)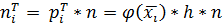 (1.32)
(1.32)